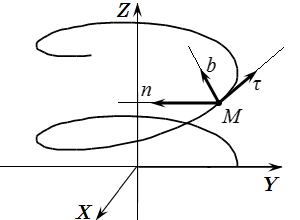
Оси естественного трехгранника Френе
Введение
На странице “Кинематика материальной точки” мы установили, что вектор скорости движения точки направлен по касательной к траектории. Вектор ускорения лежит в соприкасающейся плоскости и его можно разложить на две составляющие. Одна составляющая направлена по касательной к траектории. Вторая составляющая направлена перпендикулярно касательной, в сторону мгновенного центра кривизны траектории.
В некоторых случаях удобно ввести систему координат, связанную с текущим положением точки. Рассмотрим точку в определенный момент времени. Считаем, что нам известна траектория ее движения. Проведем через точку три прямых – касательную к траектории, главную нормаль и бинормаль. Главная нормаль перпендикулярна касательной и направлена в сторону мгновенного центра кривизны траектории. Бинормаль перпендикулярна касательной и главной нормали. Выберем систему координат с началом в точке и осями, направленными вдоль этих прямых. Такую систему координат называют естественным трехгранником Френе. Оси этой системы координат называются осями естественного трехгранника.
Орты естественного трехгранника

Пусть , и – единичные векторы, направленные вдоль касательной, главной нормали и бинормали к траектории, соответственно. Эти векторы являются ортами выбранной нами системы координат или ортами естественного трехгранника. Рассмотрим вопрос о выборе направления этих векторов.
Единичный вектор направлен вдоль касательной к траектории. Поэтому можно выбрать два взаимно противоположных направления. Самый удобный способ – это направить вдоль вектора скорости точки. Тогда
.
Однако, это не всегда можно сделать. Встречаются случаи, когда траектория движения заранее известна, а скорость – нет. Например, при движении точки по желобу внутри твердого тела под действием внешних сил. В таких случаях направление вектора выбирают заранее. Например, в сторону возрастания дуговой координаты.
Направление единичного вектора главной нормали определено однозначно. Он направлен перпендикулярно , в сторону мгновенного центра кривизны траектории.
Единичный вектор бинормали направлен перпендикулярно векторам и так, чтобы три вектора , и образовали правостороннюю систему координат:
.
Скорость и ускорение точки в трехграннике Френе
Применим формулы, которые мы вывели на странице “Кинематика материальной точки”.
;
.
То есть, в естественном трехграннике с ортами , скорость имеет одну компоненту:
.
Проекции вектора скорости на оси и трехгранника равны нулю. Проекцию скорости на направление единичного вектора касательной к траектории : , иногда называют алгебраической величиной скорости. Она отличается от модуля скорости только тем, что может иметь отрицательное значение: . При , скорость направлена вдоль вектора . При – в противоположную сторону.
Здесь и далее модуль скорости мы обозначаем либо символом с прямыми скобками , , либо просто символом без стрелки :
.
Ускорение имеет две компоненты:
,
Через них выражается касательное и нормальное ускорения:
.
Они являются проекциями вектора ускорения на оси и естественного трехгранника:
.
Их можно выразить через компоненту скорости и радиус кривизны траектории :
.
Компонента может быть как положительной (вектор сонаправлен с ), так и отрицательной (вектор противоположен ): . Компонента всегда положительна либо равна нулю: .
Проекция вектора ускорения на ось равна нулю:
.
Как определить оси естественного трехгранника
Далее мы считаем, что у нас есть неподвижная система координат . Материальная точка совершает движение. Требуется найти оси естественного трехгранника. То есть определить проекции ортов , и в системе координат .
Для координатного и векторного способов задания движения
Для координатного и векторного способов задания движения точки, формулы для определения ортов представлены на странице “Кинематика материальной точки”. На странице “Координатный способ задания движения точки” разобран пример вычисления компонентов векторов .
То есть, чтобы определить орты естественного трехгранника, нужно найти компоненты векторов скорости и нормального ускорения , применяя следующие формулы:
;
;
;
.
Далее определяем орты естественного трехгранника:
;
;
.
Для естественного способа задания движения
При естественном способе задания движения точки нам известна траектория ее движения. Поэтому перед нами стоит задача – по известной траектории, определить орты естественного трехгранника. Если траектория представляет собой простую геометрическую фигуру, например окружность, то определить векторы , и можно геометрически.
В общем, и более сложном случае, нужно представить уравнение траектории в параметрическом виде. Для этого вводим параметр . Это можно сделать многими способами. Поэтому желательно выбрать наиболее удобное представление.
Пусть, например, траекторией движения является эллипс, лежащий в плоскости :
.
Наиболее удобное параметрическое представление можно получить, если воспользоваться тригонометрической формулой:
.
Тогда уравнение траектории имеет вид:
Здесь – параметр.
Это не единственный способ получить параметрическое представление. Можно, например, разрешить уравнение эллипса относительно :
.
Применяя эту формулу, получим другое параметрическое представление:
Далее считаем, что эти параметрические уравнения описывают движение материальной точки, в котором параметр играет роль времени. Тогда, для определения осей трехгранника, можно применить формулы, применяемые для векторного и координатного способов задания движения. Вычисленные, таким образом, скорость и ускорение будут зависеть от выбранного параметрического представления. Но геометрические характеристики траектории, такие как орты , , и радиус кривизны траектории не зависят от выбранного параметрического представления.
Итак, чтобы найти орты естественного трехгранника по заданной траектории движения, нужно представить уравнение траектории в параметрическом виде и применить формулы, применяемые при координатном способе задания движения.
Пример определения ортов естественного трехгранника
Найти единичные векторы в направлении осей естественного трехгранника, а также радиус кривизны траектории, для цилиндрической винтовой линии с радиусом основания и шагом .
Решение
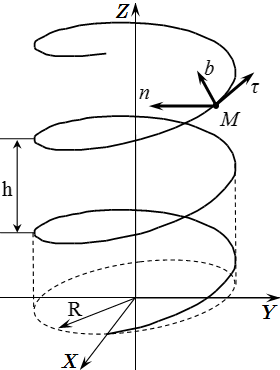
Выберем систему координат . Ось направим вдоль оси винтовой линии. Тогда уравнение линии можно представить в следующем параметрическом виде:
(1)
Здесь – параметр; . Если взять проекцию точки линии, на плоскость , то – это угол между осью и проекцией . При увеличении на , координаты и точки возвращаются в первоначальной положение, а координата увеличивается на .
Считаем, что уравнения (1) описывают движение точки по винтовой линии. Определяем кинематические величины для такого движения.
Дифференцируя уравнения (1) по , находим компоненты вектора скорости:
;
;
.
Квадрат скорости:
.
Модуль скорости:
.
Единичный вектор в направлении касательной к траектории:
.
Мы выбрали направление вектора , совпадающим с направлением скорости. Поэтому
.
Дифференцируя компоненты вектора скорости по , находим компоненты вектора ускорения:
;
;
.
Проекция ускорения на направление вектора :
.
Этот результат можно получить и более простым способом. Для этого учтем, что модуль скорости и, следовательно , не зависит от . Тогда:
.
Вектор касательного ускорения:
.
Вектор нормального ускорения:
.
Квадрат вектора нормального ускорения:
.
Модуль вектора нормального ускорения:
.
Радиус кривизны траектории:
.
Единичный вектор в направлении главной нормали траектории:
.
Единичный вектор в направлении бинормали:
.
Ответ
;
;
;
,
где .
Автор: Олег Одинцов. Опубликовано: Изменено:
