Теоремы о среднем (Ролля, Лагранжа и Коши)

Приводятся формулировки, доказательство и следствия теорем о среднем значении производной функции на отрезке. Они позволяют выразить приращение функции на отрезке через значение производной в одной из внутренних точек отрезка.

Теоремы о среднем

Теорема Ролля о нулях производной

Пусть функция
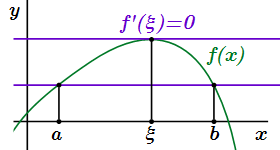
1) непрерывна при ;
2) дифференцируема при ;
3) .
Тогда существует точка такая, что производная функции в ней равна нулю:
, где .
Доказательство

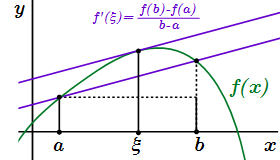
Теорема Лагранжа конечных приращений

Пусть функция
1) непрерывна при ;
2) дифференцируема при .
Тогда существует точка такая, что производная функции в ней равна угловому коэффициенту прямой, проведенной через точки и :
, где .
Или
, где .
Доказательство

Формула конечных приращений Лагранжа

– это следующая формула:
, где ;
где функция непрерывна на отрезке и дифференцируема внутри него.
Ее также можно записать в следующем виде:
,
где ; функция непрерывна на отрезке с концами и дифференцируема внутри него.

Формула бесконечно малых приращений

,
где функция дифференцируема в точке .
См. Теорема о существовании производной дифференцируемой функции

Теорема Коши является обобщением теоремы Лагранжа, на случай, в котором функция задана параметрическим способом: . Если обозначить , и воспользоваться формулой производной параметрически заданной функции, то формула конечных приращений Коши примет вид приращений Лагранжа:
.

Упрощение формулировок

В формулировках теорем требуется, чтобы функция была непрерывна на отрезке и дифференцируема во внутренних точках этого отрезка. На самом деле, если функция дифференцируема, в какой либо точке, то она и непрерывна в этой точке. Поэтому в условиях теорем важно, чтобы функция была непрерывна только на концах отрезка – во внутренних точках она непрерывна автоматически.
См. Теорема о непрерывности дифференцируемой функции

Если же функция дифференцируема и на концах отрезка, то требование непрерывности вообще является излишним. Тогда, для применения этих теорем, нет необходимости исследовать функцию на непрерывность.

Только если функция определена на определенном отрезке, или составлена из кусков, требуется исследование на непрерывность в тех точках, в которых нет производных (но могут быть односторонние производные).

Следствия из теоремы Лагранжа

Доказательство от противного. Если существуют две точки с неравными значениями функции: , то по теореме Лагранжа между и существует точка с отличной от нуля производной:
.

Для доказательства достаточно применить предыдущее свойство к функции .

Почему теоремы называются теоремами о среднем

Полное название – «Теоремы о среднем значении производной на отрезке». Называются они так потому, что дробь является средним значением производной функции на отрезке . Тогда теорема Лагранжа утверждает, что, при указанных условиях, существует внутренняя точка отрезка , в которой производная функции равна ее среднему значению на этом отрезке.

Теорема Ролля является частным случаем, когда среднее значение производной равняется нулю. Но она является отправным пунктом для доказательства теорем Лагранжа и Коши.

В более общей теореме Коши, выражение является средним значением производной , записанным в параметрическом виде: . Тогда производная y по x выражается через производные функций и по формуле:
.
См. Производная функции, заданной параметрическим способом

Покажем, что можно рассматривать как среднее значение производной на отрезке . Чтобы не загромождать рассуждений положим, что функция дифференцируема на всем отрезке, включая его концы, то есть при . Разобьем на n равных отрезков , каждый из которых имеет длину . Пронумеруем их от a к b. Тогда отрезок под номером m расположен при . Производная функции в точке :
.
См. Теорема о существовании производной дифференцируемой функции

Найдем среднее значение совокупности n величин :

;
(4.1)   .

Рассмотрим предельный переход .
Тогда .
Среднее , при , можно рассматривать как среднее значение производной на отрезке :
.
Тогда из (4.1) получаем:
.

Геометрический смысл теоремы Лагранжа

Построим график функции . Через точки и проведем прямую. Если дифференцируема на , то к графику можно провести касательную, параллельную прямой AB. Причем эта касательная проходит через одну из внутренних точек .

Действительно, угловой коэффициент прямой AB равен
.
Согласно теореме Лагранжа, существует такая точка , производная в которой равна
.
Согласно теореме о геометрическом смысле производной, через эту точку можно провести касательную с угловым коэффициентом .

Доказательство теорем

Сначала приведем для справок формулировку теоремы Ферма. Затем, на ее основе докажем теорему Ролля, используя которую, докажем теоремы Лагранжа и Коши.

Теорема о необходимом условии экстремума функции (Ферма)

Если точка является точкой строгого или нестрогого локального экстремума функции ,
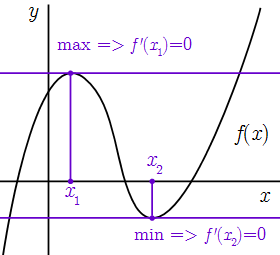
и она дифференцируема в этой точке,
то ее производная в равна нулю:
.
Доказательство

Теорема Ролля о нулях производной

Все теоремы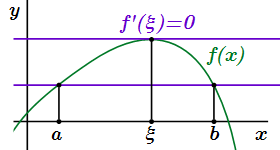

Пусть функция
1) непрерывна при ;
2) дифференцируема при ;
3) .
Тогда существует точка такая, что производная функции в ней равна нулю:
, где .

Теорема Лагранжа конечных приращений

Все теоремы

Пусть функция
1) непрерывна при ;
2) дифференцируема при .
Тогда существует точка такая, что производная функции в ней равна угловому коэффициенту прямой, проведенной через точки и :
, где .
Или
, где .

Использованная литература:
А.М. Тер-Крикоров, М.И. Шабунин. Курс математического анализа. Москва, ФИЗМАТЛИТ, 2001.

Автор: Олег Одинцов.     Опубликовано: 30-05-2024