Теоремы Вейерштрасса о непрерывных на отрезке функциях
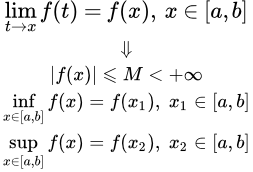
Теоремы
то она ограничена на этом отрезке.
Доказательство
достигает на нем своих нижней и верхней граней.
Или, что тоже самое, достигает на отрезке своего минимума и максимума.
То есть существуют такие точки x1, x2 ∈ [a,b], так что для любого x ∈ [a,b], выполняются неравенства:
f(x1) ≤ f(x) ≤ f(x2).
Доказательство
Различие между максимумом (минимумом) и верхней (нижней) гранью заключается в том, что максимум (минимум) принадлежит множеству значений функции, а верхняя (нижняя) грань может не принадлежать этому множеству. Пусть, например, на открытом интервале X = {x : 0 < x < 1} задана функция f (x) = x. На этом интервале функция имеет верхнюю и нижнюю грани:
supx ∈ X f (x) = 1, infx ∈ X f (x) = 0.
Но максимума и минимума не имеет. Действительно, для любого x0 ∈ X всегда можно указать такие числа x1 = (x0 + 1) / 2 и x2 = x0 / 2, принадлежащие X, значения функции от которых будут больше и меньше x0:
f (x1) > f (x0), f (x2) < f (x0).
На отрезке X = {x : 0 ≤ x ≤ 1} функция имеет как верхнюю и нижнюю грани, так максимум и минимум:
supx ∈ X f (x) = maxx ∈ X f (x) = f (1) = 1, infx ∈ X f (x) = minx ∈ X f (x) = f (0) = 0.
Также верхняя (нижняя) грань может равняться плюс (минус) бесконечности: +∞ (–∞), а максимум (минимум) не может быть бесконечным числом.
Доказательство теорем
Первая теорема Вейерштрасса об ограниченности непрерывной на отрезке функции
Все теоремы Если функция f непрерывна на отрезке [a,b],то она ограничена на этом отрезке.
Допустим противное. Пусть функция f (x) не ограничена при x ∈ [a, b]. Это означает, что для любого M > 0 всегда можно найти такое xM ∈ [a, b], что | f (xM) | > M.
Задавая M последовательно значения M = 1, 2, 3,..., n,..., мы получим последовательность {xn}, элементы которой принадлежат отрезку [a, b]: xn ∈ [a, b], и для которых
(1.1) | f (xn) | > n.
Рассмотрим последовательность { | f (xn) | }. Учитывая (1.1), и поскольку limn → ∞ n = +∞, то по свойству неравенств бесконечно больших последовательностей,
(1.2) limn → ∞ | f (xn) | = +∞.
Рассмотрим последовательность {xn}. Согласно теореме Больцано - Вейерштрасса, из нее можно выделить подпоследовательность, сходящуюся к некоторому числу c. Эту подпоследовательность обозначим как {xnk}. Тогда
limk → ∞ xnk = c.
Поскольку a ≤ xnk ≤ b, то по свойству пределов последовательностей, связанных неравенствами,
a ≤ c ≤ b.
Далее, { | f (xnk) | } есть подпоследовательность последовательности { | f (xn) | }, которая имеет бесконечный предел +∞ (см. (1.2)). Поскольку предел любой подпоследовательности равен пределу последовательности, то
limk → ∞ | f (xnk) | = limn → ∞ | f (xn) | = +∞.
Итак, мы нашли последовательность xnk, сходящуюся при k → ∞ к числу c ∈ [a, b]. И для этой последовательности
(1.3) limk → ∞ | f (xnk) | = +∞.
Это противоречит определению непрерывности по Гейне, согласно которому предел последовательности { f (xnk)} должен равняться конечному числу – значению функции в точке c:
limn → ∞ f (xnk) = f (c).
Тогда и предел модуля (1.3), также должен равняться конечному числу:
limn → ∞ | f (xnk) | = | f (c) | .
Теорема доказана.
Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Все теоремы Непрерывная на отрезке [a,b] функция fдостигает на нем своих нижней и верхней граней.
Или, что тоже самое, достигает на отрезке своего минимума и максимума.
То есть существуют такие точки x1, x2 ∈ [a,b], так что для любого x ∈ [a,b], выполняются неравенства:
f(x1) ≤ f(x) ≤ f(x2).
Доказательство для максимума
Докажем сначала теорему для максимума. Пусть число M является верхней гранью значений функции f (x) на отрезке [a, b]: M = supx ∈ [a,b] f (x). Согласно первой теореме Вейерштрасса ⇑, функция f ограничена на этом отрезке. Поэтому M – конечное число. Нам нужно показать, что
M = f (c), где c ∈ [a, b].
По определению верхней грани, выполняются следующие условия:
1) f (x) ≤ M для всех x ∈ [a, b];
2) для любого ε > 0, существует xε ∈ [a, b] такое, что
f (xε) > M – ε.
Положим ε = 1 / n. Тогда существует такая точка xn ∈ [a, b], для которой
M – 1 / n < f (xn) ≤ M.
Вычтем из всех частей неравенств число M:
–1 / n < f (xn) – M ≤ 0.
Умножим на –1:
1 / n > M – f (xn) ≥ 0.
Поменяем неравенства местами:
0 ≤ M – f (xn) < 1n.
Таким образом мы построили последовательности {xn} и { f (xn)}, элементы которых удовлетворяют неравенствам:
a ≤ xn ≤ b;
0 ≤ M – f (xn) < 1n.
Покажем, что limn → ∞ f (xn) = M.
Для этого изменим последнее неравенство и введем числа N и ε:
| M – f (xn) | < 1n < 1N < ε.
Отсюда видно, что для любого ε > 0 всегда можно указать натуральное число N > 1 / ε. Тогда для всех n > N, | M – f (xn) | < ε. Согласно определению предела последовательности это означает, что
(2.1) limn → ∞ f (xn) = M.
Рассмотрим последовательность {xn}. Согласно теореме Больцано - Вейерштрасса, из нее можно выделить подпоследовательность, сходящуюся к некоторому числу c. Эту подпоследовательность обозначим как {xnk}. Тогда
limk → ∞ xnk = c.
Поскольку a ≤ xnk ≤ b, то по свойству пределов последовательностей, связанных неравенствами,
a ≤ c ≤ b.
Рассмотрим последовательность { f (xnk)}. Она является подпоследовательностью последовательности { f (xn)}. Поскольку { f (xn)} сходится к числу M, то и любая ее подпоследовательность сходится к этому же числу. Поэтому
(2.2) limk → ∞ f (xnk) = M.
Поскольку при k → ∞, xnk → c ∈ [a, b], то согласно определению непрерывности по Гейне, (2.3) limk → ∞ f (xnk) = f (c).
Поскольку сходящаяся последовательность может иметь только один предел, то из (2.2) и (2.3) следует, что
M = f (c).
То есть верхняя грань M равна значению функции в одной из точек отрезка [a, b]. Поэтому M также является максимальным значением функции на этом отрезке.
Для максимума теорема доказана.
Доказательство для минимума
Доказательство теоремы для минимума аналогично предыдущему. Изложим его вкратце.
Пусть m = infx ∈ [a,b] f (x). Тогда
1) f (x) ≥ m для всех x ∈ [a, b];
2) для любого ε > 0, существует xε ∈ [a, b] такое, что
f (xε) < m + ε.
Полагая ε = 1 / n, мы получим последовательности {xn}, и { f (xn)} элементы которых удовлетворяют неравенствам:
a ≤ xn ≤ b;
0 ≤ f (xn) – m < 1n.
из последней строчки видно, что
(2.4) limn → ∞ f (xn) = m.
Из последовательности {xn} выделим подпоследовательность {xnk}, сходящуюся к некоторому числу c:
limk → ∞ xnk = c.
Поскольку a ≤ xnk ≤ b, то по свойству неравенств,
a ≤ c ≤ b.
Рассмотрим последовательность { f (xnk)}. Она является подпоследовательностью последовательности { f (xn)}. Поскольку { f (xn)} сходится к числу m, то и любая ее подпоследовательность сходится к этому же числу. Поэтому
(2.5) limk → ∞ f (xnk) = m.
Поскольку при k → ∞, xnk → c ∈ [a, b], то согласно определению непрерывности по Гейне, (2.6) limk → ∞ f (xnk) = f (c).
Поскольку сходящаяся последовательность может иметь только один предел, то
m = f (c).
То есть нижняя грань m равна значению функции в одной из точек отрезка [a, b]. Поэтому m также является минимальным значением функции на этом отрезке.
Теорема доказана.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено: