Геометрический смысл производной
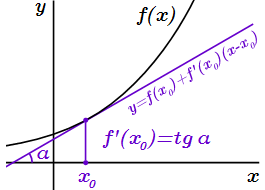
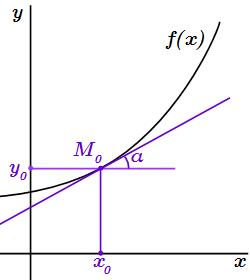
то график функции y = f (x) имеет наклонную касательную в x0, тангенс угла которой с осью абсцисс равен производной: f ′(x0) = tg α. Угол считается положительным, если график касательной возрастает; угол отрицательный – если убывает. Другими словами, производная функции в точке x0 равна угловому коэффициенту касательной графика функции в точке x0, а уравнение касательной имеет вид:
y = f (x0) + f ′(x0)(x – x0).
2. Если производная функции f (x) в точке x = x0 равна бесконечности: f ′(x0) = ∞,
то в этой точке график имеет вертикальную касательную, описываемую уравнением
x = x0.
Доказательство
Исследование геометрического смысла производной
Исследуем геометрический смысл производной функции y = f (x) при некотором, заранее заданном значении аргумента x = x0. Считаем, что функция имеет конечную производную в x0. Тогда существует окрестность точки x0, в которой функция определена и имеет конечные значения. Проводим оси координат. По оси абсцисс будем откладывать значения переменной x; по оси ординат – значения переменной y. Строим график функции y = f (x) в окрестности точки x0.
Отмечаем точку M0 (x0, y0), где y0 = f (x0). Выбираем на графике произвольную точку M1 (x1, y1), где y1 = f (x1).
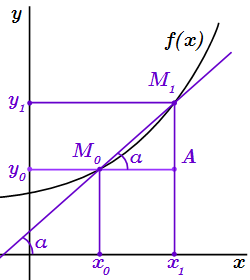
Проводим через M0 и M1 секущую M0 M1. Далее через M0 проводим прямую, параллельную оси x, а через M1 – параллельную оси y. Точку пересечения этих прямых обозначим как A.
Треугольник M0 AM1 – прямоугольный. Пусть α – угол между сторонами M0 A и M0 M1. Тогда
AM1M0 A = y1 – y0x1 – x0 = tg α.
Но y1 – y0x1 – x0 = f (x1) – f (x0)x1 – x0 = Δ f Δx. Отсюда
(1) f (x1) – f (x0)x1 – x0 = tg α.
Поскольку прямая M0 A параллельна оси x, то угол α является углом между секущей и осью абсцисс x.
Теперь выполним предельный переход x1 → x0. При таком переходе точка M1 будет стремиться к M0, приближаясь к ней сколь угодно близко. Сама секущая также будет меняться, поворачиваясь вокруг точки M0. При x1 → x0 она будет стремиться к некоторой предельной прямой, которая называется касательной к графику в точке M0. Угол наклона α касательной определяется из (1), устремляя x1 → x0. Воспользовавшись определением производной, имеем:
tg α = limx1 → x0 f (x1) – f (x0)x1 – x0 = f ′(x0).
Таким образом, производная функции в точке x0 равна тангенсу угла между касательной, проведенной через эту точку, и осью абсцисс.
Как известно из аналитической геометрии, уравнение прямой с угловым коэффициентом tg α, и проходящей через точку (x0, y0) имеет вид:
y = y0 + tg α ⋅ (x – x0).
Подставляя y0 = f (x0), tg α = f ′(x0), получаем уравнение касательной к графику в точке x0:
y = f (x0) + f ′(x0)(x – x0).
Теорема о геометрическом смысле производной
1. Если существует конечная производная функции f (x) в точке x = x0,то график функции y = f (x) имеет наклонную касательную в x0, тангенс угла которой с осью абсцисс равен производной: f ′(x0) = tg α (см. рисунок). Угол считается положительным, если график касательной возрастает; угол отрицательный – если убывает. Другими словами, производная функции в точке x0 равна угловому коэффициенту касательной графика функции в точке x0, а уравнение касательной имеет вид:
y = f (x0) + f ′(x0)(x – x0).
2. Если производная функции f (x) в точке x = x0 равна бесконечности: f ′(x0) = ∞,
то в этой точке график имеет вертикальную касательную, описываемую уравнением
x = x0.
Возьмем на графике функции y = f (x) произвольную точку M1 (x1, y1), отличную от M0 (x0, y0). Здесь y0 = f (x0), y1 = f (x1). Проведем через точки M0 и M1 прямую, которая является секущей. Составим уравнение прямой, проходящей через эти точки:
(Т1) y – y0 = y1 – y0x1 – x0 (x – x0) = f (x1) – f (x0)x1 – x0 (x – x0).
Считаем, что x и x0 – постоянные, то есть заранее заданные числа. Выполняем предельный переход x1 → x0. Применим определение производной:
y – y0 = limx1 → x0 f (x1) – f (x0)x1 – x0 (x – x0) = f ′(x0)(x – x0);
(Т2) y = f (x0) + f ′(x0)(x – x0).
Мы видим, что при x1 → x0, график секущей (Т1) преобразуется в прямую (Т2), которая является касательной. Как видно из (Т2), касательная является прямой, проходящей через точку M0 с угловым коэффициентом, равным производной функции в x0. Из аналитической геометрии известно, что угловой коэффициент прямой равен тангенсу угла α между осью абсцисс и этой прямой. Тогда:
f ′(x0) = tg α.
2. Пусть в точке x0 производная функции равна бесконечности: f ′(x0) = limx1 → x0 f (x1) – f (x0)x1 – x0 = ∞.
Перепишем (Т1) и выполним предельный переход, воспользовавшись свойством бесконечно большой функции.
x – x0 = y – y0 f (x1) – f (x0)x1 – x0;
x – x0 = limx1 → x0 y – y0 f (x1) – f (x0)x1 – x0 = 0;
x = x0.
Это уравнение прямой, проходящей через точку x0 параллельно оси ординат.
Теорема доказана.
Производная равна бесконечности
Если производная в x0 равна бесконечности, то касательная вертикальна, но возможны три случая: 1) Производная равна плюс бесконечности: f ′(x0) = +∞; 2) производная равна минус бесконечности: f ′(x0) = –∞; 3) производная равна бесконечности без определенного знака: f ′(x0) = ∞, f ′(x0) ≠ ±∞.
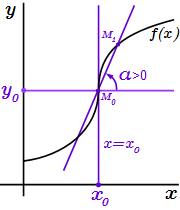
1) Если производная равна плюс бесконечности: f ′(x0) = +∞, то угол между осью абсцисс и любой секущей, проходящей через точку (x0, y0) положителен: 0 < α < +π / 2, и стремится к +π / 2 при M1 → M0. Здесь подразумевается, что вторая точка графика M1, через которую проходит секущая, расположена достаточно близко к x0.
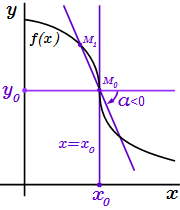
2) Если производная равна минус бесконечности: f ′(x0) = –∞, то угол между осью абсцисс и любой секущей, проходящей через точку (x0, y0) отрицателен: –π / 2 < α < 0, и стремится к –π / 2 при M1 → M0.
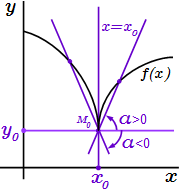
3) Если производная равна бесконечности без определенного знака: f ′(x0) = ∞, f ′(x0) ≠ ±∞, то углы наклона секущих, проходящих через вторую точку слева и справа от (x0, y0), имеют разные знаки.
Автор: Олег Одинцов. Опубликовано: Изменено: