Что такое радиус-вектор, и чем он отличается от других векторов
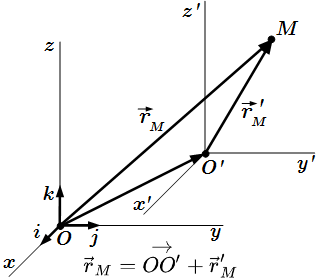
Понятие радиус-вектора
- Радиус-вектор точки M
- – это вектор в координатном пространстве, проведенный из начала системы координат O к точке M:
.
Радиус-вектор вводится для того, чтобы представить положение точки в пространстве в виде вектора. Этим он отличается от других векторов, которые могут описывать различные физические величины, такие как скорости, ускорения, силы, и т.п.
В математическом смысле радиус-вектор обладает следующими свойствами.
1. Является вектором. То есть при поворотах системы координат, его компоненты преобразуются как компоненты вектора, по формулам (1).
2. При параллельном переносе системы координат, при котором ее начало перемещается из точки O в O′, компоненты радиус-вектора точки M преобразуются по закону (2):
,
где – компоненты радиус-вектора в системах Oxyz и O′x′y′z′; – радиус-вектор точки O′ в системе Oxyz.
Рассмотрим эти пункты более подробно.
1. Радиус-вектор – это вектор
Как и всякий вектор, радиус-вектор в трехмерном пространстве описывается тремя числами. Существует два варианта представления вектора.
В первом способе, вектор представлен тремя (контравариантными) координатами , которые его однозначно определяют по формуле:
,
где – базисные векторы, определяющие направления координатных осей.
Во втором способе вектор задается тремя проекциями на оси координат, которые называются компонентами или ковариантными координатами.
Если в качестве выбрать единичные векторы , и выбрать прямоугольную систему координат, то эти два способа эквивалентны – контравариантные координаты равны компонентам (ковариантным координатам). В дальнейшем мы будем использовать только прямоугольную систему координат, и в качестве базисных векторов выбирать единичные векторы , направленные вдоль осей координат . Для записи вектора будем использовать одну из следующих форм:
.
По сути вектор в трехмерном пространстве является множеством, состоящим из трех чисел – компонент. Главным отличием вектора от других множеств является то, что его компоненты изменяются по одному закону при повороте системы координат относительно начала O. Это приводит к тому, что все векторы преобразуются как единое целое, сохраняя неизменным направление друг относительно друга и относительное расположение вершин. То есть вся совокупность векторов поворачивается по единому правилу.
При таком повороте изменяются направления координатных осей и, следовательно, векторов . Пусть – их новые направления после поворота, а – новые координаты. Тогда
.
Поочередно умножая скалярно это уравнение на , и пользуясь ортогональностью этих векторов, получаем закон преобразования компонент вектора при повороте системы координат относительно ее начала:
(1)
Поскольку векторы и единичной длины, то их попарные произведения равны косинусам углов между ними.
2. Преобразование компонент при переносе начала системы координат
Отличие радиус-вектора от других векторов, заключается в том, что при параллельном переносе начала системы координат, его компоненты преобразуются по закону:
(2) .
Или в развернутом виде:
(2*)
Здесь – компоненты вектора .
Так, если в процессе вычислений, мы получили векторное выражение, то можно определить, определяет ли это выражение точку в пространстве координат или нет. Если полученное выражение является радиус-вектором (то есть его компоненты при повороте системы координат преобразуются по закону (1), а при параллельном переносе – по закону (2)), то это точка в пространстве координат. Если преобразование (2) не выполняется, но выполняется (1), то это вектор, который не соответствует точке в координатном пространстве.
О пространствах
При решении задач, как правило, используется не одно, а несколько видов пространств – координатное, скоростей, ускорений, сил и т.п. В начале мы определяем систему координат в базовом пространстве, для чего произвольно выбираем ее начало O, и направления осей, вводя единичные векторы . Такое пространство будем называть координатным пространством, или пространством системы координат. Положения точек в этом пространстве описываются с помощью радиус-векторов. Используя их, мы вводим другие векторные механические величины такие как скорость, ускорение, сила и т.п. Тем самым получаем другие пространства – пространство скоростей, ускорений, сил, и т. п. Для каждого такого пространства строится своя система координат с выбранными ранее направлениями осей , а начало отсчета соответствует нулевому значению физической величины. Например, для пространства скоростей, мы выбираем систему координат, в которой начало соответствует нулевой скорости точки, а по осям абсцисс, ординат и аппликат, откладываются проекции скорости на оси Ox, Oy, Oz:
.
То, что для каждой физической величины нужно свое пространство уже следует из того, что различные величины имеют разные размерности. Мы не можем, например, в координатной системе Oxyz, в которой компоненты точек измеряются в метрах, откладывать компоненты скорости, которые измеряются в м/с, как не можем складывать расстояния со скоростями.
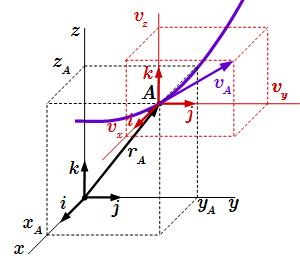
Однако векторы, принадлежащие разным пространствам, часто изображают в одной системе координат, что нередко приводит к путанице. Пусть, например, материальная точка находится в точке A и имеет скорость . В этом случае, для наглядности, и точку A, и ее скорость изображают на одном рисунке, откладывая начало вектора скорости из точки A. При этом, чтобы не загромождать рисунок, отбрасывают некоторые детали, которые считаются сами собой разумеющимися. А эти детали заключаются в том, что здесь должны присутствовать две системы координат – одна для расстояний между объектами, и одна для скоростей. То есть подразумевается, что имеется еще одна система координат скоростей, оси которой параллельны координатным осям Oxyz. Для удобства ее начало помещают в точку A, но сама она с этой точкой связи не имеет. То есть здесь имеются два вектора: и из различных пространств. Для первого мы выбираем систему координат произвольным образом, а система координат второго вектора строится из первой: началом отсчета является нулевая скорость, а направления осей совпадают с направлениями первой системы координат. То есть вектор только для нагладности откладывается из точки A, на самом деле он откладывается из начала системы координат скоростей, которая никак не связана с точкой A.
Простые примеры
1. Пусть M и C – две точки пространства, и – их радиус-векторы. Рассмотрим их разность . Поскольку компоненты векторов и при повороте системы координат преобразуются по закону (1), то компоненты их разности также преобразуются по этому закону:

В этом легко убедиться раскрыв скобки и сгруппировав слагаемые. Это означает, что величина является вектором.
Проверим, является ли радиус-вектором. Для этого выполним параллельный перенос системы координат из начала O в O′. Выписываем преобразования компонент:
,
;
.
Компоненты вектора не изменились. То есть они не преобразуются по закону (2). Поэтому величина радиус-вектором не является; этот вектор не указывает на точку пространства, а лишь указывает на смещение точки M относительно точки C.
В том, что вектор не определяет точки пространства, можно убедиться и другим путем. Выберем систему координат с началом в точке C. Тогда . Вектор указывает на точку M. Теперь возьмем систему координат с началом в точке M: ; вектор указывает на другую точку. Возникло противоречие. То есть не является радиус-вектором, хотя является вектором.
2. Рассмотрим сумму . Аналогично предыдущему заключаем, что является вектором.
Находим закон преобразования компонент при параллельном переносе системы координат из начала O в O′:
,
;
.
Компоненты вектора также не преобразуются по закону (2). Поэтому и не является радиус-вектором.
3. Наконец рассмотрим полусумму . Тем же способом, что и ранее убеждаемся, что является вектором.
Выполняем параллельный перенос системы координат:
,
;
;
.
Компоненты преобразуются по закону (2). Поэтому он является радиус-вектором, и определяет точку в пространстве – середину отрезка CM.
Примеры из механики
Скорость точки. Пусть положение точки в момент времени t задано ее радиус-вектором . Скорость точки определяется как его производная по времени:
.
Это предел от разности радиус-векторов и , деленной на . Как мы выяснили выше, разность радиус-векторов является вектором, но не радиус-вектором. Поэтому скорость точки радиус-вектором не является.
Центр масс (и центр тяжести) системы n материальных точек определяется по формуле:
.
Здесь – массы точек; – их радиус-векторы.
Поскольку он представляет собой сумму векторов, умноженных на постоянные коэффициенты, то его компоненты, при повороте системы координат, преобразуются также как векторы . Это означает, что центр масс является вектором.
Проверим, является ли центр масс радиус-вектором. Выполним параллельный перенос начала системы координат из точки O в O′. Компоненты радиус-векторов преобразуются по закону (2):
.
Находим закон преобразования компонент центра масс.
;
.
Вектор преобразуется по закону (2), то есть является радиус-вектором. Поэтому он определяет точку в пространстве длин. Для центра тяжести это означает, что он связан с другими точками, и является геометрической характеристикой твердого тела.
Автор: Олег Одинцов. Опубликовано:
