Все картинки раздела «Кинематика»
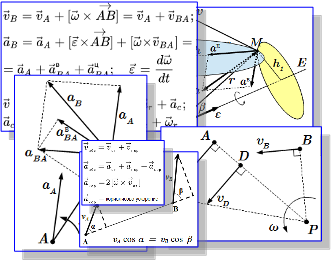
Здесь собраны все изображения раздела «Кинематика» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением.
Содержание
См. также:
Все понятия, определения и теоремы кинематики (обзорная страница)
Кинематика. Все определения, понятия, законы и теоремы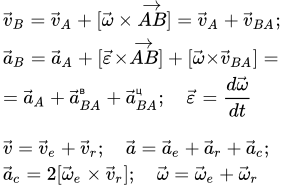
Все определения, понятия, законы и теоремы кинематики в одной странице. Материал делится на четыре основных раздела: кинематика точки, кинематика твердого тела, кинематика сложного движения точки и кинематика сложного движения твердого тела. 
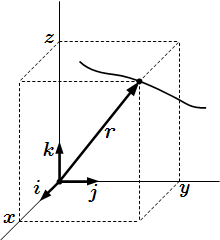Радиус-вектор точки и ее траектория. 
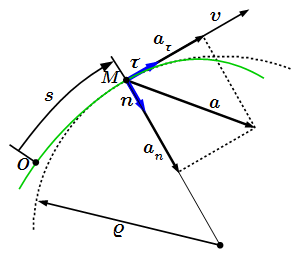Скорость и тангенциальное ускорение точки M направлены по касательной к траектории. Нормальное ускорение – перпендикулярно. 
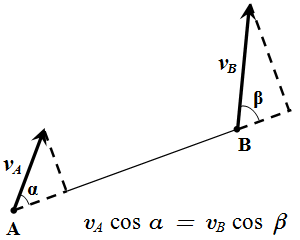Теорема о проекциях скоростей двух точек твердого тела на прямую 
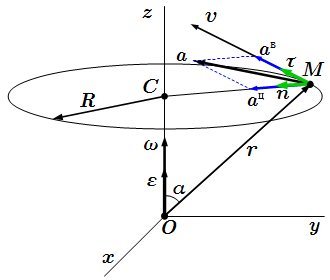Скорость и ускорение точек твердого тела при вращении вокруг неподвижной оси Oz. 
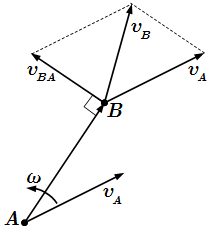Скорости точек при плоском движении твердого тела. 
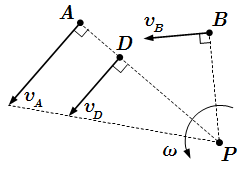Мгновенный центр скоростей P является мгновенной осью вращения твердого тела. 
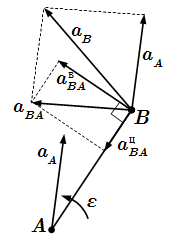Ускорения точек при плоском движении твердого тела. 
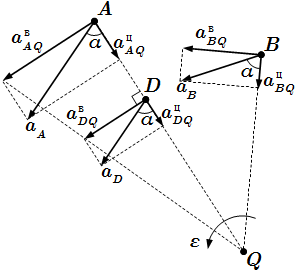Мгновенный центр ускорений. 
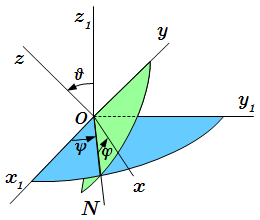Углы Эйлера. Оси K и K′ не показаны. 
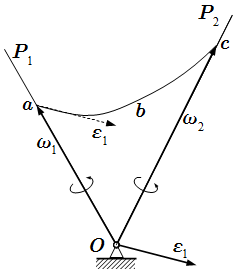Угловое ускорение ε является касательной к годографу abc угловой скорости. P1, P2 – мгновенные оси вращения. 
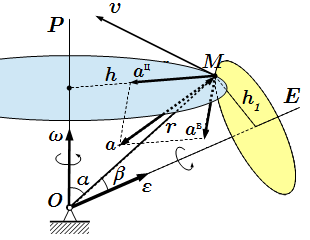Ускорение при сферическом движении твердого тела. 
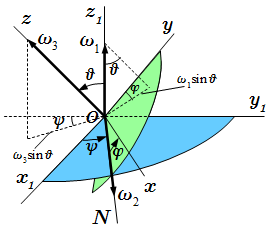Связь угловых скоростей с углами Эйлера. 
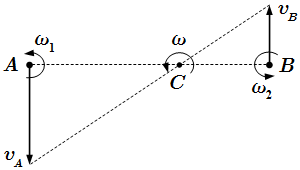Вращения направлены в одну сторону. 
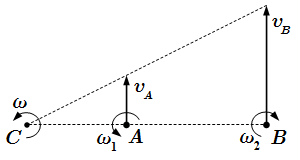Вращения направлены в противоположные стороны, ω1 > ω1. 
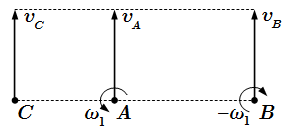Пара вращений. Угловые скорости равны по модулю и противоположны по направлению.
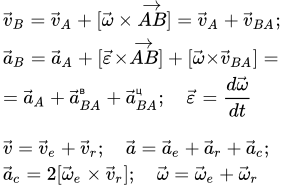Все определения, понятия, законы и теоремы кинематики в одной странице. Материал делится на четыре основных раздела: кинематика точки, кинематика твердого тела, кинематика сложного движения точки и кинематика сложного движения твердого тела. Радиус-вектор точки и ее траектория. Скорость и тангенциальное ускорение точки M направлены по касательной к траектории. Нормальное ускорение – перпендикулярно. Теорема о проекциях скоростей двух точек твердого тела на прямую Скорость и ускорение точек твердого тела при вращении вокруг неподвижной оси Oz. Скорости точек при плоском движении твердого тела. Мгновенный центр скоростей P является мгновенной осью вращения твердого тела. Ускорения точек при плоском движении твердого тела. Мгновенный центр ускорений. Углы Эйлера. Оси K и K′ не показаны. Угловое ускорение ε является касательной к годографу abc угловой скорости. P1, P2 – мгновенные оси вращения. Ускорение при сферическом движении твердого тела. Связь угловых скоростей с углами Эйлера. Вращения направлены в одну сторону. Вращения направлены в противоположные стороны, ω1 > ω1. Пара вращений. Угловые скорости равны по модулю и противоположны по направлению. Другие страницы
Что такое радиус-вектор, и чем он отличается от других векторов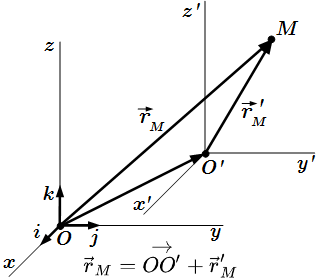
Понятие радиус-вектора и его свойства. На примерах разобрано его отличие от других векторов. 
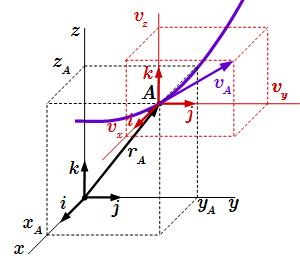Система координат скоростей никак не связана с точкой A, хотя вектор скорости часто откладывают из этой точки. Кинематика материальной точки
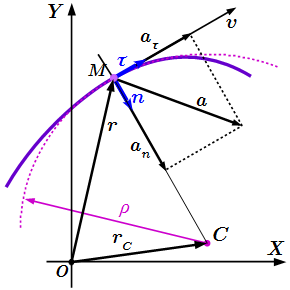Даны основные формулы кинематики материальной точки, их вывод и изложение теории. 
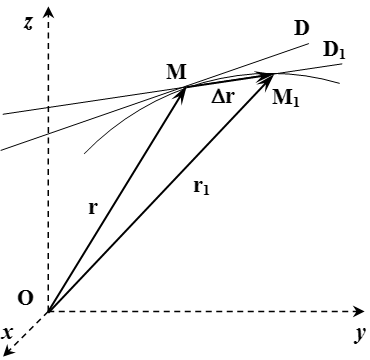Касательная к траектории точки 
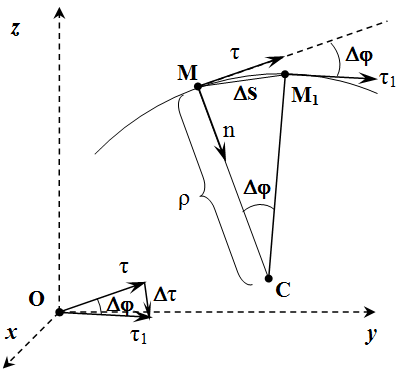Радиус кривизны траектории Координатный способ задания движения точки
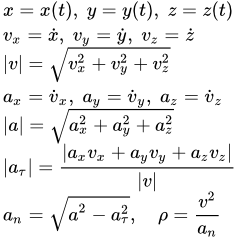Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали по заданным зависимостям координат от времени. Пример решения задачи, в которой по заданным уравнениям движения нужно определить скорость и ускорение точки. Также определяется радиус кривизны траектории, касательная, нормаль и бинормаль. 
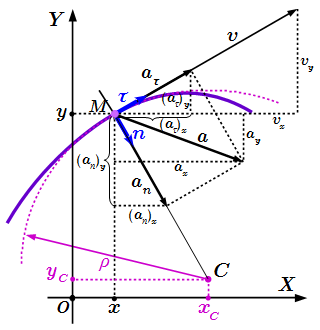Скорость и ускорение точки M при координатном способе задания движения 
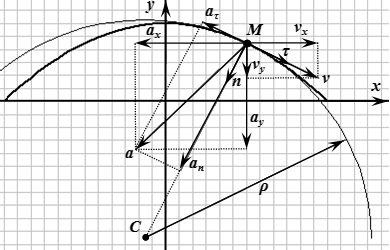Определение скорости и ускорения точки M Векторный способ задания движения точки
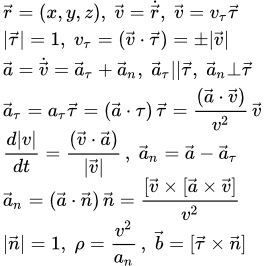Связь векторного способа задания движения точки с координатным. Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали при векторном способе задания движения точки. Скорость и ускорение точки M при векторном способе задания движения Оси естественного трехгранника Френе
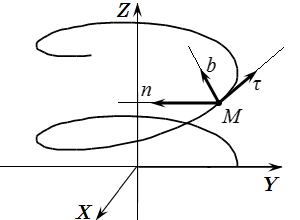Определение естественного трехгранника Френе. Проекции скорости и ускорения точки на его оси. Пример определения ортов естественного трехгранника. 
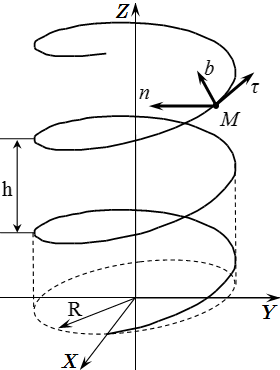Трехгранник винтовой линии Естественный способ задания движения точки
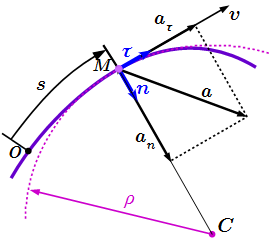Естественный способ задания движения точки – определение и основные формулы. Пример решения задачи. 
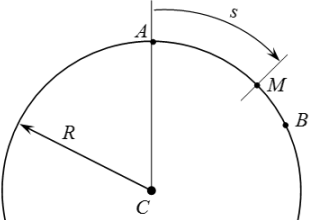Условие задачи 
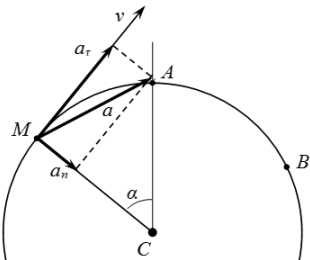Скорость и ускорение при движении по окружности Теорема о проекциях скоростей двух точек твердого тела на прямуюТеорема о проекциях скоростей двух точек твердого тела на прямую. Доказательство теоремы. Пример решения задачи.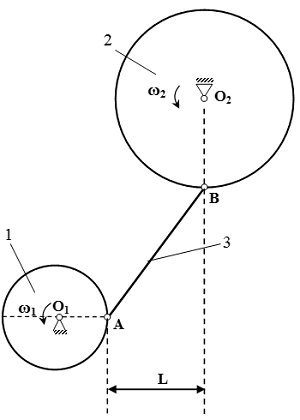 
Рисунок к условию задачи 
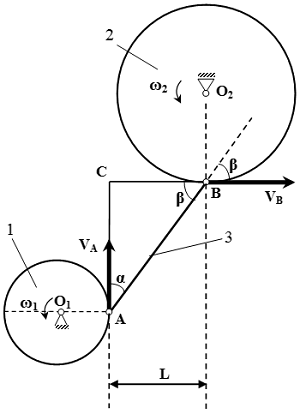Рисунок к решению задачи Скорость и ускорение точек твердого тела, совершающего поступательное и вращательное движения
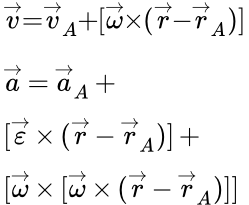Формулы скорости (ускорения) точек твердого тела, выраженные через скорость (ускорение) полюса и угловую скорость (ускорение). Вывод этих формул из принципа, что расстояния между любыми точками тела, при его движении, остаются постоянными. 
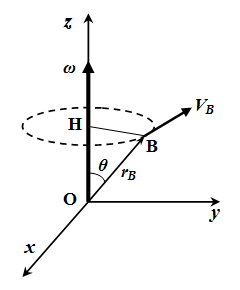ω – это вектор угловой скорости твердого тела. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи
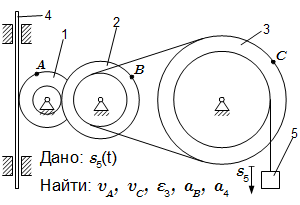Приводятся основные законы и формулы, применяемые при решении задач на определение скоростей и ускорений точек твердого тела при вращательном движении вокруг неподвижной оси. Рассмотрен пример подробного решения задачи. В ней дан механизм, состоящий из колес, рейки и груза, соединенных нитями и зубчатой передачей. Требуется найти скорости и ускорения точек, принадлежащих звеньям этого механизма. 
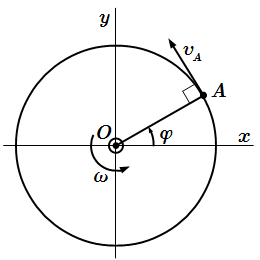Скорость точки при вращательном движении тела вокруг неподвижной оси 
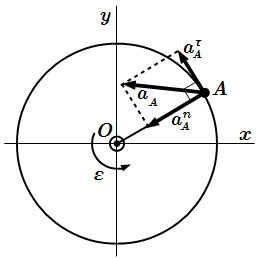Ускорение точки при вращательном движении тела вокруг неподвижной оси 
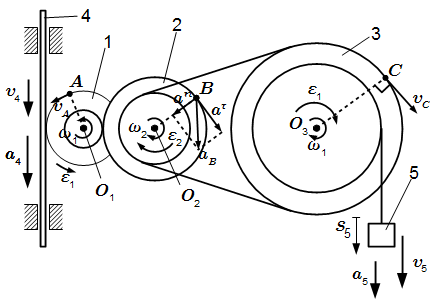Решение задачи Кинематический анализ плоского механизма – пример решения задачи
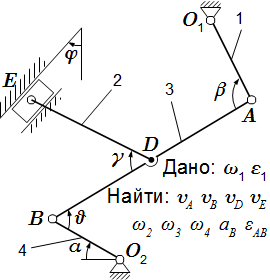Рассмотрены методы определения скоростей и ускорений звеньев плоского многозвенного механизма. При этом используется понятие мгновенного центра скоростей, теоремы о проекциях скоростей, о скоростях точек и об ускорениях точек плоской фигуры. Подробно разобран пример решения задачи на тему 'кинематический анализ многозвенного механизма'. 
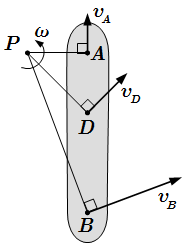Рис. 1. Мгновенный центр скоростей P. Рис. 2. Теорема о проекциях скоростей.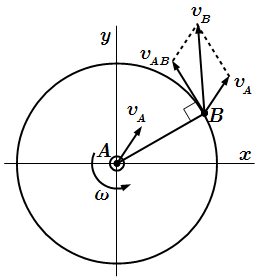 
Рис. 3. Теорема о скоростях точек плоской фигуры 
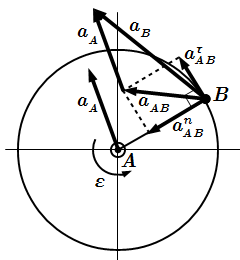Рис. 4. Теорема об ускорениях точек плоской фигуры 
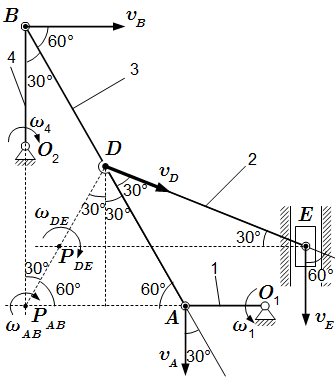Рис. 6. Кинематический анализ многозвенного механизма. Решение с помощью мгновенного центра скоростей 
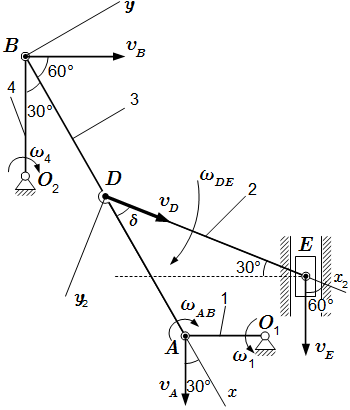Рис. 7. Кинематический анализ многозвенного механизма. Применение теоремы о проекциях скоростей и теоремы о скоростях точек плоской фигуры 
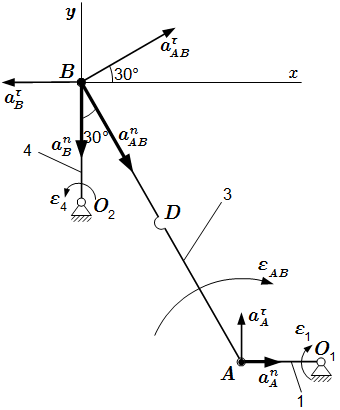Рис. 8. Определение ускорений с помощью теоремы об ускорениях точек плоской фигуры Сложное движение точки. Теорема Кориолиса
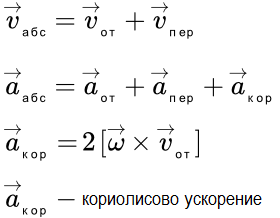Определение сложного (составного) движения точки. Определение абсолютного, относительного и переносного движения, скорости и ускорения. Доказательство теоремы о сложении скоростей и теоремы Кориолиса о сложении ускорений. Кориолисово (поворотное) ускорение. 
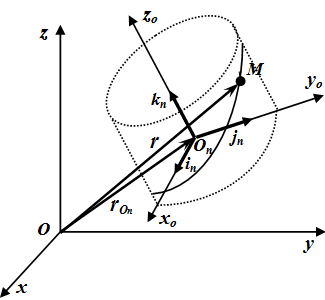Сложное движение. Точка M движется относительно движущегося тела. Сложное движение точки. Пример решения задачи
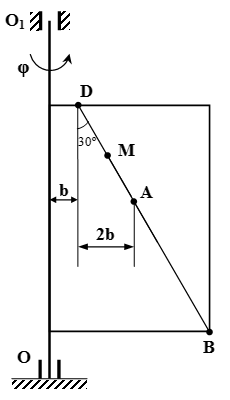Рассмотрен пример решения задачи со сложным движением точки. Точка движется по прямой вдоль пластины. Пластина вращается вокруг неподвижной оси. Определяется абсолютная скорость и абсолютное ускорение точки. 
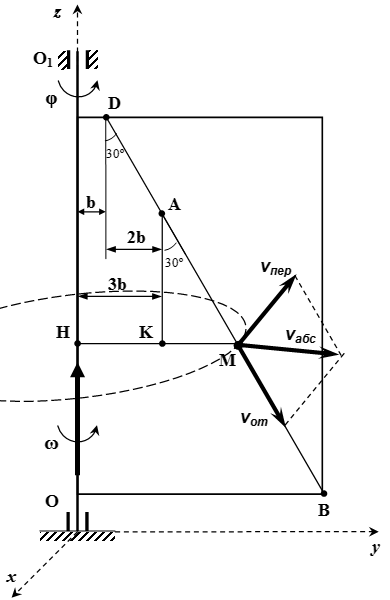Относительная, переносная и абсолютная скорость точки M 
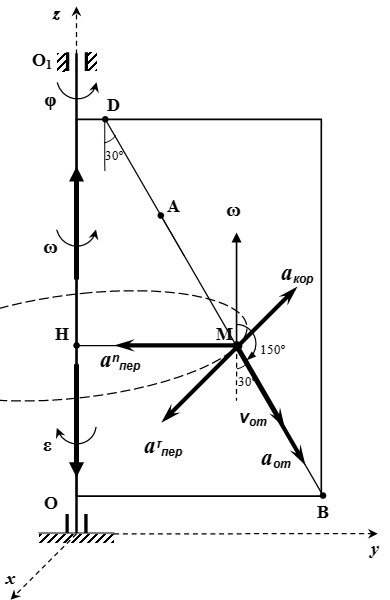Относительное, переносное, кориолисово и абсолютное ускорение точки M
Понятие радиус-вектора и его свойства. На примерах разобрано его отличие от других векторов. Система координат скоростей никак не связана с точкой A, хотя вектор скорости часто откладывают из этой точки. Кинематика материальной точкиДаны основные формулы кинематики материальной точки, их вывод и изложение теории. Касательная к траектории точки Радиус кривизны траектории Координатный способ задания движения точки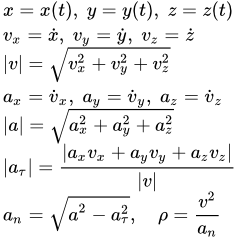Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали по заданным зависимостям координат от времени. Пример решения задачи, в которой по заданным уравнениям движения нужно определить скорость и ускорение точки. Также определяется радиус кривизны траектории, касательная, нормаль и бинормаль. Скорость и ускорение точки M при координатном способе задания движения Определение скорости и ускорения точки M Векторный способ задания движения точки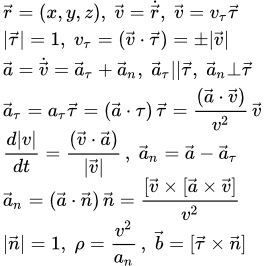Связь векторного способа задания движения точки с координатным. Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали при векторном способе задания движения точки. Скорость и ускорение точки M при векторном способе задания движения Оси естественного трехгранника ФренеОпределение естественного трехгранника Френе. Проекции скорости и ускорения точки на его оси. Пример определения ортов естественного трехгранника. Трехгранник винтовой линии Естественный способ задания движения точкиЕстественный способ задания движения точки – определение и основные формулы. Пример решения задачи. Условие задачи Скорость и ускорение при движении по окружности Теорема о проекциях скоростей двух точек твердого тела на прямуюТеорема о проекциях скоростей двух точек твердого тела на прямую. Доказательство теоремы. Пример решения задачи. Рисунок к условию задачи Рисунок к решению задачи Скорость и ускорение точек твердого тела, совершающего поступательное и вращательное движения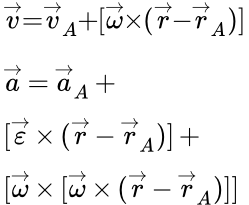Формулы скорости (ускорения) точек твердого тела, выраженные через скорость (ускорение) полюса и угловую скорость (ускорение). Вывод этих формул из принципа, что расстояния между любыми точками тела, при его движении, остаются постоянными. ω – это вектор угловой скорости твердого тела. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачиПриводятся основные законы и формулы, применяемые при решении задач на определение скоростей и ускорений точек твердого тела при вращательном движении вокруг неподвижной оси. Рассмотрен пример подробного решения задачи. В ней дан механизм, состоящий из колес, рейки и груза, соединенных нитями и зубчатой передачей. Требуется найти скорости и ускорения точек, принадлежащих звеньям этого механизма. Скорость точки при вращательном движении тела вокруг неподвижной оси Ускорение точки при вращательном движении тела вокруг неподвижной оси Решение задачи Кинематический анализ плоского механизма – пример решения задачиРассмотрены методы определения скоростей и ускорений звеньев плоского многозвенного механизма. При этом используется понятие мгновенного центра скоростей, теоремы о проекциях скоростей, о скоростях точек и об ускорениях точек плоской фигуры. Подробно разобран пример решения задачи на тему 'кинематический анализ многозвенного механизма'. Рис. 1. Мгновенный центр скоростей P. Рис. 2. Теорема о проекциях скоростей. Рис. 3. Теорема о скоростях точек плоской фигуры Рис. 4. Теорема об ускорениях точек плоской фигуры Рис. 6. Кинематический анализ многозвенного механизма. Решение с помощью мгновенного центра скоростей Рис. 7. Кинематический анализ многозвенного механизма. Применение теоремы о проекциях скоростей и теоремы о скоростях точек плоской фигуры Рис. 8. Определение ускорений с помощью теоремы об ускорениях точек плоской фигуры Сложное движение точки. Теорема Кориолиса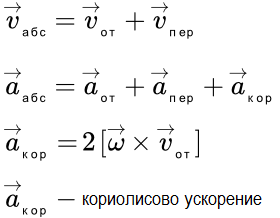Определение сложного (составного) движения точки. Определение абсолютного, относительного и переносного движения, скорости и ускорения. Доказательство теоремы о сложении скоростей и теоремы Кориолиса о сложении ускорений. Кориолисово (поворотное) ускорение. Сложное движение. Точка M движется относительно движущегося тела. Сложное движение точки. Пример решения задачиРассмотрен пример решения задачи со сложным движением точки. Точка движется по прямой вдоль пластины. Пластина вращается вокруг неподвижной оси. Определяется абсолютная скорость и абсолютное ускорение точки. Относительная, переносная и абсолютная скорость точки M Относительное, переносное, кориолисово и абсолютное ускорение точки M ❮ Статика в картинках | Динамика материальной точки в картинках
См. также: