Дифференциальное уравнение Риккати
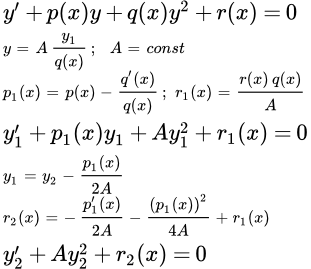
- Дифференциальное уравнение Риккати
- – это уравнение вида
.
Общее решение этого уравнения можно получить только в некоторых частных случаях.
Решение дифференциального уравнения Риккати при известном частном решении
Рассмотрим дифференциальное уравнение Риккати:
(1) .
Пусть известно его частное решение :
Тогда подстановкой уравнение Риккати (1) приводится к уравнению Бернулли:
;
;
;
;
.
Это уравнение Бернулли с n = 2.
Свойства уравнения Риккати
Не меняет вид уравнения:
- Произвольное преобразование независимого переменного:
- Произвольное дробно-линейное преобразование зависимого переменного:
При таких подстановках уравнение также является уравнением Риккати, но с другими функциями p, q, r.
Вид общего решения
Общее решение уравнения Риккати есть дробно-линейная функция от произвольной постоянной:
И наоборот если общее решение уравнения есть дробно-линейная функция от произвольной постоянной, то соответствующее уравнение есть уравнение Риккати.
Упрощение уравнения Риккати
Снова рассмотрим дифференциальное уравнение Риккати:
(1) .
Подстановкой
,
где А – постоянная, оно приводится к виду:
(2) ,
где .
Далее, подстановкой
оно приводится к виду:
(3)
где .
Упрощенное уравнение Риккати
Упрощенное уравнение Риккати – это уравнение вида:
(4) ,
где A, B – постоянные. Оно интегрируется при
,
где – целое.
Покажем это. Сделаем подстановку:
;
.
Подставляем в (4):
.
Умножаем на :
(5) .
Но
.
Подставляем в (5):
Или
(6)
где
.
Уравнение (6) интегрируется при
.
Для этого разделим его на и перепишем в следующем виде:
;
;
.
Это уравнение с разделяющимися переменными. Оно легко интегрируется.
При уравнение (6) можно преобразовать двумя путями.
- Подстановкой , где , оно преобразуется к виду: .
- Подстановкой , где , оно преобразуется к виду:
Таким образом, при , где n - целое число, ряд подстановок приводит к полному решению.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано:
