Дифференциальное уравнение Якоби

Дано определение дифференциального уравнения Якоби и рассмотрен метод его решения.

Содержание

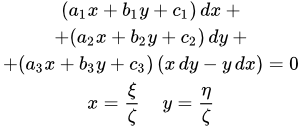
Определение

Дифференциальное уравнение Якоби: – это уравнение вида
(a₁ x + b₁ y + c₁ ) dx + (a₂ x + b₂ y + c₂ ) dy + (a₃ x + b₃ y + c₃ ) (xdy – ydx ) = 0 ,
где a₁ , b₁ , c₁ , a₂ , b₂ , c₂ , a₃ , b₃ , c₃ – постоянные коэффициенты.

Метод решения

Рассмотрим уравнение Якоби:
(1) (a₁ x + b₁ y + c₁ ) dx + (a₂ x + b₂ y + c₂ ) dy + (a₃ x + b₃ y + c₃ ) (xdy – ydx ) = 0 .
Делаем подстановку:
x = ξζ ; y = ηζ .
Тогда:
dx = ζdξ – ξdζζ² ; dy = ζdη – ηdζζ² ;
xdy – ydx = ξζ ⋅ ζdη – ηdζζ² – ηζ ⋅ ζdξ – ξdζζ² = ξζdη – ξηdζζ³ – ηζdξ – ηξdζζ³ =
= ξdη – ηdξζ² .
Подставляем в (1):
( a₁ ξζ + b₁ ηζ + c₁ ) ζdξ – ξdζζ² + ( a₂ ξζ + b₂ ηζ + c₂ ) ζdη – ηdζζ² + ( a₃ ξζ + b₃ ηζ + c₃ ) ξdη – ηdξζ² = 0 .
Умножаем на ζ³ и вводим обозначения:
s₁ = a₁ ξ + b₁ η + c₁ ζ; s₂ = a₂ ξ + b₂ η + c₂ ζ; s₃ = a₃ ξ + b₃ η + c₃ ζ .
Получаем:
s₁ (ζdξ – ξdζ ) + s₂ (ζdη – ηdζ ) + s₃ (ξdη – ηdξ ) = 0

Это уравнение можно записать в виде равенства нулю определителя:

	dη	dζ
ξ	η	ζ
– s₂	s₁	s₃

| = 0

Определитель равен нулю, если строки линейно зависимы. Тогда нужно положить:
(2)

{

dξdt = – s₂ = – a₂ ξ – b₂ η – c₂ ζ

dηdt = s₁ = a₁ ξ + b₁ η + c₁ ζ

dζdt = s₃ = a₃ ξ + b₃ η + c₃ ζ

где t – новая вспомогательная переменная. Тем самым мы получили систему линейных уравнений, которая решается простыми методами. Решение этих уравнений дает три равенства с ξ, η, ζ, t . Присоединив к ним формулы x = ξ / ζ, y = η / ζ , мы получаем пять уравнений. Исключая из них ξ, η, ζ и t , найдем общий интеграл исходного уравнения (1).

В наиболее распространенном случае решение уравнений (2) дается равенствами:
α₁ ξ + β₁ η + γ₁ ζ = C₁ e^λ₁ t
α₂ ξ + β₂ η + γ₂ ζ = C₂ e^λ₂ t
α₃ ξ + β₃ η + γ₃ ζ = C₃ e^λ₃ t
Возводим их в степень (λ₂ – λ₃ ) , (λ₃ – λ₁ ) , (λ₁ – λ₂ ) , соответственно:
(α₁ ξ + β₁ η + γ₁ ζ ) ^{λ₂ – λ₃} = C₁ ^{λ₂ – λ₃} ⋅ (e^λ₁ t ) ^{λ₂ – λ₃} = C₁ ^{λ₂ – λ₃} ⋅ e^{λ₁ (λ₂ – λ₃ ) t}
(α₂ ξ + β₂ η + γ₂ ζ ) ^{λ₃ – λ₁} = C₂ ^{λ₃ – λ₁} ⋅ (e^λ₂ t ) ^{λ₃ – λ₁} = C₂ ^{λ₃ – λ₁} ⋅ e^{λ₂ (λ₃ – λ₁ ) t}
(α₃ ξ + β₃ η + γ₃ ζ ) ^{λ₁ – λ₂} = C₃ ^{λ₁ – λ₂} ⋅ (e^λ₃ t ) ^{λ₁ – λ₂} = C₃ ^{λ₁ – λ₂} ⋅ e^{λ₃ (λ₁ – λ₂ ) t}
Перемножая эти равенства, и замечая, что
e^{λ₁ (λ₂ – λ₃ ) t} ⋅ e^{λ₂ (λ₃ – λ₁ ) t} ⋅ e^{λ₃ (λ₁ – λ₂ ) t} = e^{(λ₁ λ₂ – λ₁ λ₃ + λ₂ λ₃ – λ₂ λ₁ + λ₃ λ₁ – λ₃ λ₂ ) t} = e⁰ = 1
и вводя новую постоянную
C = C₁ ^{λ₂ – λ₃} ⋅ C₂ ^{λ₃ – λ₁} ⋅ C₃ ^{λ₁ – λ₂}
получаем:
(α₁ ξ + β₁ η + γ₁ ζ ) ^{λ₂ – λ₃} ⋅ (α₂ ξ + β₂ η + γ₂ ζ ) ^{λ₃ – λ₁} ⋅ (α₃ ξ + β₃ η + γ₃ ζ ) ^{λ₁ – λ₂} = C
В каждом множителе выносим ζ за скобки. Поскольку
ζ^{λ₂ – λ₃} ⋅ ζ^{λ₃ – λ₁} ⋅ ζ^{λ₁ – λ₂} = 1 ,
то, переходя к переменным x и y, получаем общий интеграл уравнения Якоби в виде:
(α₁ x + β₁ y + γ₁ ) ^{λ₂ – λ₃} ⋅ (α₂ x + β₂ y + γ₂ ) ^{λ₃ – λ₁} ⋅ (α₃ x + β₃ y + γ₃ ) ^{λ₁ – λ₂} = C .

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов. Опубликовано: 16-08-2012