Обобщенные однородные дифференциальные уравнения первого порядка
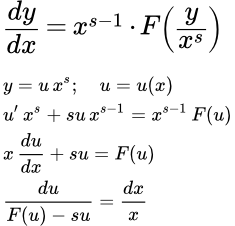
- Обобщенное однородное дифференциальное уравнение первого порядка
- Дифференциальное уравнение первого порядка называется обобщенно однородным, если существует такое отличное от нуля и единицы число s, s ≠ 0, s ≠ 1 , при котором это уравнение не меняет своего вида после замены
x → tx, y → t s y ,
где t – постоянная. При такой замене производная умножается на t s – 1 :
y ′ ≡ dydx → d (t s y ) d (tx ) = t s t ⋅ dydx = t s – 1 y ′ .
Уравнения, разрешенные относительно производной, приводятся к уравнениям с разделяющимися переменными подстановкой
(5) y = ux s , где u – функция от x .
Кроме этого, любое обобщенно однородное уравнение приводятся к уравнениям, не содержащих независимую переменную подстановками
(6) x = e t , y = ue st ,
где u – функция от t .
В общем виде, обобщенно однородные уравнения можно записать так:
(1) f (x, y, y ′ ) = 0 , где функция f обладает следующим свойством:
(2) f (tx, t s y, t s – 1 y ′ ) = t p f (x, y, y ′ ) .
Здесь t может зависеть от переменных x и y .
Обобщенно однородные уравнения, разрешенные относительно производной, можно представить в следующем виде:
(3) M (x s , y ) ⋅ xx s ⋅ y ′ + N (x s , y ) = 0 ,
где M (u, v ) и N (u, v ) – однородные функции с равными показателями однородности.
Также, такие уравнения можно записать, используя только одну произвольную функцию F :
(4) y ′ = x s – 1 F ( yx s ) .
Как определить, является ли дифференциальное уравнение обобщенным однородным
Для того, чтобы определить, является ли дифференциальное уравнение обобщенным однородным, нужно ввести постоянную t и сделать замену
x → tx, y → t s y .
Если удастся выбрать такое значение s , при котором постоянная t сократится, то это обобщенное однородное дифференциальное уравнение. Изменение производной y′ при такой замене имеет вид:
y ′ = dydx → d ( t s y ) d (tx ) = t s dyt dx = t s – 1 dydx .
Пример
Определить, является ли данное уравнение обобщенным однородным:
(x 6 – y 4 ) y ′ = 3x 5 y .
Решение
Делаем замену x → tx, y → t s y, t ′ → t s – 1 y ′ :
( (tx ) 6 – (t s y ) 4 ) t s – 1 y ′ = 3(tx ) 5 t s y ;
( t 6 x 6 – t 4s y 4 ) t s – 1 y ′ = 3t s + 5 x 5 y .
Разделим на t s+5 :
t – 6 ( t 6 x 6 – t 4s y 4 ) y ′ = 3x 5 y ;
( x 6 – t 4s – 6 y 4 ) y ′ = 3x 5 y .
Уравнение не будет содержать t , если
4s – 6 = 0 , s = 3/2 .
Поскольку при s = 3/2 , t сократилось, то это обобщенное однородное уравнение.
Методы решения
Общий вид обобщенно однородных уравнений
Сначала проясним вопрос, почему в определении тестовая переменная t является постоянной, а в (2) может быть функцией. На самом деле форма (1) не описывает все возможные варианты записи обобщенно однородных уравнений. В более общем случае, дифференциальное уравнение можно представить в виде различных комбинаций, составленных из переменных и дифференциалов. Тогда, чтобы иметь возможность выносить тестовую переменную t за знаки дифференциалов, ее нужно считать постоянной. Но в форме (1) она уже вынесена из под дифференциалов, поэтому t может быть функцией.
Во всех этих и дальнейших рассуждениях подразумевается, что значения x, y и t таковы, что при них определены все используемые функции.
Легко убедиться, что формы (1), (3) и (4) описывают обобщенно однородные уравнения. Для этого сделаем в них замены x → tx, y → t s y, y → t s – 1 y ′ .
Для формы (1), используем свойство (2):
f (x, y, y ′ ) = 0 →
f (tx, t s y, t s – 1 y ′ ) = 0 ;
t p f (x, y, y ′ ) = 0 ;
f (x, y, y ′ ) = 0 .
t сократилось – это обобщенно однородное уравнение.
Для формы (3), используем определение однородной функции и учтем, что показатели однородности функций M и N равны:
M (x s , y ) ⋅ xx s ⋅ y ′ + N (x s , y ) = 0 →
M (t s x s , t s y ) ⋅ txt s x s ⋅ t s – 1 y ′ + N (t s x s , t s y ) = 0 ;
t ps M (x s , y ) ⋅ xx s ⋅ y ′ + t ps N (x s , y ) = 0 ;
M (x s , y ) ⋅ xx s ⋅ y ′ + N (x s , y ) = 0 .
t сократилось.
Для формы (4):
y ′ = x s – 1 F ( yx s ) →
t s – 1 y ′ = t s – 1 x s – 1 F ( t s yt s x s ) ;
y ′ = x s – 1 F ( yx s ) .
Здесь также t сократилось.
Теперь покажем, как от формы (3) перейти к (4). Разделим (3) на x – s + 1 M (x s , y ) , воспользуемся однородностью функций M и N , и что их показатели однородности равны. При M (x s , y ) ≠ 0 имеем:
y ′ = – N (x s , y ) x – s + 1 M (x s , y ) = – x s – 1 N ( x s , x s ⋅ yx s ) M ( x s , x s ⋅ yx s ) = – x s – 1 x ps N ( 1, yx s ) x ps M ( 1, yx s ) =
– x s – 1 N ( 1, yx s ) M ( 1, yx s ) = x s – 1 F ( yx s ) ,
где F (z ) = – N (1, z ) M (1, z ) .
Поскольку мы отбросили случай M (x s , y ) = 0 , то эти формы не эквивалентны. Уравнение (3) может содержать дополнительные решения, определяемые из уравнения M (x s , y ) = 0 . Остальные решения этих уравнений совпадают.
Решение уравнений, разрешенных относительно производной
Рассмотрим разрешенное относительно производной обобщенное однородное дифференциальное уравнение первого порядка в форме (4):
dydx = x s – 1 F ( yx s ) .
Покажем, что оно приводится к однородному уравнению с помощью подстановки
t = x s .
Действительно,
dt = dx s = dx s dx dx = sx s – 1 dx .
Отсюда
dx = x – s + 1 s dt ; dydx = sx s – 1 dydt .
Подставляем в исходное уравнение:
sx s – 1 dydt = x s – 1 ⋅ F ( yt ) ;
dydt = 1s F ( yt ) .
Это однородное уравнение. Оно решается заменой
y = ut ,
где u – функция от t .
Однако, при решении задач, проще сразу применить подстановку
(5) y = ux s , где u – функция от x .
Также можно ввести переменные t, u и сделать замену
(6) x = e t , y = ue st .
Покажем, что при этом уравнение
(4) y ′ = x s – 1 F ( yx s )
приводится к разделяющимся переменным.
Выразим производную y ′ = dydx через переменные t и u .
(e st ) ′ ≡ de st dt = de st d (st ) ⋅ d (st ) dt = e st ⋅ s = se st ;
dydt = (ue st ) ′t = u ′e st + u (e st ) ′ = u ′e st + sue st = (u ′ + su ) e st ;
dxdt = (e t ) ′ = e t ;
y ′ ≡ dydx = dydt dxdt = (u ′ + su ) e st e t = (u ′ + su ) e (s – 1 ) t ;
(7) dydx = (u ′ + su ) e (s – 1 ) t .
Подставляем в (4):
yx s = ue st (e t ) s = ue st e st = u ;
y ′ = x s – 1 F ( yx s ) ;
(u ′ + su ) e (s – 1 ) t = e (s – 1 ) t F (u ) ;
u ′ + su = F (u ) ;
dudt = F (u ) – su ;
duF (u ) – su = dt, F (u ) – su ≠ 0 .
И мы получили уравнение с разделяющимися переменными.
Уравнения, неразрешенные относительно производной
Покажем, что любые обобщенно однородные уравнения, в том числе и неразрешенные относительно производной, приводятся к уравнениям, не содержащих независимую переменную подстановками
(6) x = e t , y = ue st ,
где u – функция от t .
Ранее мы уже нашли выражение производной dydx через переменные t и u :
(7) dydx = (u ′ + su ) e (s – 1 ) t .
Подставим в (1) и применим свойство (2).
f (x, y, y ′ ) = 0 ;
f ( e t , ue st , (u ′ + su ) e (s – 1 ) t ) = 0 ;
f ( e t ⋅ 1, (e t ) s ⋅ u, (e t ) s – 1 ⋅ (u ′ + su ) ) = 0 ;
(e t ) p ⋅ f (1, u, u ′ + su ) = 0 ;
f (1, u, u ′ + su ) = 0 .
Мы получили уравнение, содержащее в явном виде только зависимую переменную u и ее производную u ′ = dudt . Оно не содержит зависимую переменную t .
См. Решение дифференциальных уравнений, не содержащих одну из переменных
Пример решения обобщенного однородного дифференциального уравнения первого порядка
Решить дифференциальное уравнение
(П.1) (1 – xy ) xy ′ + y (1 + xy ) = 0 .
Решение первым способом
Проверим, является ли данное уравнение обобщенным однородным. Для этого в (П.1) делаем замену:
y → t s· y , x → t·x , y′ → t s–1 y′ .
(1 – tx t s y ) tx t s – 1 y ′ + t s y (1 + tx t s y ) = 0 .
Разделим на t s :
(1 – t s + 1 xy ) xy ′ + y (1 + t s + 1 xy ) = 0 .
t сократится, если положить s = –1 . Значит – это обобщенное однородное уравнение.
Делаем подстановку
y = ux s = ux – 1 , где u – функция от x .
y ′ = ( ux – 1 ) ′ = u ′x – 1 + u ( x – 1 ) ′ = u ′x – 1 + u ⋅ (– 1 ) ⋅ x – 2 = u ′x – 1 – u x – 2 .
Подставляем в исходное уравнение:
(П.1) (1 – xy ) xy ′ + y (1 + xy ) = 0 ;
( 1 – xux – 1 ) x ( u ′x – 1 – ux – 2 ) + ux – 1 ( 1 + xux – 1 ) = 0 ;
( 1 – u ) ( u ′ – ux – 1 ) + ux – 1 ( 1 + u ) = 0 .
Умножим на x и раскрываем скобки:
( 1 – u ) ( xu ′ – u ) + u ( 1 + u ) = 0 ;
( 1 – u ) xu ′ – u + u 2 + u + u 2 = 0 ;
(u – 1 ) x dudx = 2u 2 .
Разделяем переменные – умножаем на dx и делим на xu 2 . При u ≠ 0 имеем:
(u – 1 ) duu 2 = 2 dxx .
Интегрируем, пользуясь таблицей интегралов:
∫ (u – 1 ) duu 2 = 2 ∫ dxx ;
∫ (u – 1 ) duu 2 = ∫ duu – ∫ u – 2 du = ln | u | – 1– 2 + 1 u – 2 + 1 = ln | u | + 1u ;
2 ∫ dxx = 2 ln | x | = ln x 2 ;
ln | u | + 1u = ln x 2 + C .
Потенцируем:
| u | e 1u = e C x 2 .
Заменим постоянную e C → C и уберем знак модуля, поскольку выбор нужного знака определяется выбором знака постоянной С :
u e 1u = C x 2 .
Возвращаемся к переменной y . Подставляем u = xy :
xy e 1xy = C x 2 .
Делим на x :
(П.2) y e 1xy = C x .
Когда мы делили на u 2 , то предполагали, что u ≠ 0 . Теперь рассмотрим случай u = xy = 0 , или y = 0 .
Легко проверить, что постоянная функция y = 0 удовлетворяет исходному уравнению (П.1). Поэтому она является его решением. Поскольку это решение не входит в (П.2), то добавим его к полученному общему интегралу.
Ответ
y e 1xy = C x ;
y = 0 .
Решение вторым способом
Теперь решим уравнение подстановкой
(6) x = e t , y = ue st ,
перейдя к новым переменным t и u .
Выше мы нашли выражение производной y ′ = dydx через переменные t и u :
(7) dydx = (u ′ + su ) e (s – 1 ) t .
Для s = – 1 подстановки примут вид.
x = e t , y = ue – t , y ′ = (u ′ – u ) e – 2t .
Подставляем в исходное уравнение и решаем его.
(1 – xy ) xy ′ + y (1 + xy ) = 0 ;
(1 – e t ue – t ) e t (u ′ – u ) e – 2t + ue – t (1 + e t ue – t ) = 0 ;
(1 – u ) (u ′ – u ) + u (1 + u ) = 0 ;
(1 – u ) u ′ – u + u 2 + u + u 2 = 0 ;
(1 – u ) dudt + 2u 2 = 0 ;
(1 – u ) duu 2 = – 2dt, u ≠ 0 ;
∫ ( 1u 2 – 1u ) du = – 2 ∫ dt ;
– 1u – ln | u | = – 2t + C ;
ln | u | + 1u = 2t – C ;
| u | e 1u = e 2t e – C ;
e – C → C ;
ue 1u = Ce 2t = C (e t ) 2 ;
e t = x, u = e t y = xy ;
xye 1xy = Cx 2 ;
ye 1xy = Cx .
Осталось рассмотреть случай u = xy = 0 . В результате получаем частное решение y = 0 .
Ответ
y e 1xy = C x ;
y = 0 .
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено: