Понятие и формулы координат центра тяжести тела
Центр тяжести – это важнейшая геометрическая характеристика твердого тела. С его помощью можно заменить распределенные силы тяжести, действующие на отдельные точки тела, одной равнодействующей, равной весу тела, приложенной к его центру тяжести.
Сила тяжести
Сила тяжести возникает вследствие гравитационного притяжения между телом и планетой, и ее влияние необходимо учитывать во многих задачах механики. Мы будем рассматривать наиболее часто встречающийся случай силы тяжести на Земле, на высоте уровня мирового океана. Для подавляющего числа задач силы тяжести, действующие на материальные точки тела, можно считать параллельными, и их можно выразить через массу точки m и ускорение свободного падения по формуле:
.
Вследствие вращения, Земля имеет форму эллипсоида, приплюснутого на полюсах, отчего ускорение свободного падения на уровне моря зависит от географической широты. Оно имеет максимальное значение g = 9,832177 м/с2 на полюсах и минимальное g = 9,780318 м/с2 на экваторе. Во многих задачах такое различие не существенно, и можно использовать стандартное значение, принятое при построении систем единиц, которое составляет g = 9,80665 м/с2. Это значение примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В расчетах мы будем округлять его до трех значащих цифр: g = 9,81 м/с2.
Понятие центра тяжести тела
Итак, мы приняли, что вблизи поверхности земли, на материальную точку массы m, действует сила тяжести, определяемая по формуле:
,
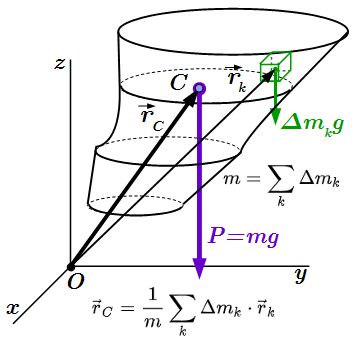
где – постоянный вектор, направленный вниз. Если тело состоит из n материальных точек Ak, то на каждую из них действует сила . Тогда, согласно теореме о центре параллельных сил, эта система сил имеет равнодействующую , направленную параллельно силам . Ее модуль равен сумме модулей сил, и называется весом тела:
(1) .
Равнодействующая приложена к центру параллельных сил C, который в данном случае называется центром тяжести тела. Его радиус-вектор определяется по формуле:
(2) ,
где – радиус-вектор точки Ak. Как мы выяснили на странице «Центр системы параллельных сил», вектор определяет точку C, связанную с телом. Поэтому центр тяжести также связан с телом и являеется его геометрической характеристикой.
Как видно из (2), вектор зависит от модулей сил , но не от их направлений. Если мы выберем систему координат, связанную с телом, то при его повороте будут изменяться направления сил. При этом компоненты вектора , а с ним и положение центра тяжести будет неизменным. То есть при любом положении тела равнодействующая проходит через точку C, радиус-вектор которой определяется по формуле (2). Это свойство лежит в основе определения центра тяжести.
- Центр тяжести твердого тела
- – это точка, связанная с телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела, при любом положении тела в пространстве.
- Вес тела
- – это абсолютное значение равнодействующей сил тяжести частиц, составляющих тело.
Согласно (2), координаты центра тяжести определяются по формулам:
(3) .
Здесь – координаты точек тела.
Центр тяжести C связан с телом. Однако его положение может находиться за его пределами. Например, при наличии полости.
Центр тяжести и центр масс
В расчетах удобно выразить силы тяжести , действующие на точки тела через их массы : . Тогда формулы (1) - (3) примут вид:
(4) – масса тела;
(5) ;
(6) .
Две последние формулы совпадают с определением другой важной величины – центра масс системы материальных точек. Из них видно, что центром тяжести тела является его центр масс. Однако понятие центра тяжести относится только к твердым телам, или которые можно считать твердыми, используя принцип отвердевания. В отличие от него, понятие центра масс относится к любым системам материальных точек, и является более общим.
Можно было подумать, что понятие центра тяжести будет отлично от центра масс в случае неоднородных гравитационных полей, в которых вектор не является постоянным, а имеет разное значение в различных точках тела. Но в таком случае центра тяжести вообще может не существовать. В более общем случае силы могут быть не параллельными. И даже если они имеют равнодействующую, то при повороте тела, линии действия равнодействующих могут не пересекаться в одной точке.
Еще один интересный случай может возникнуть, когда тело помещено в жидкость или газ. Тогда на него действует выталкивающая сила, равная весу вытесняемой жидкости. То есть сила притяжения к земле такого тела будет отличаться от той, которая вычисляется по формуле . Но и в этом случае удобно не смешивать, а разделить эти силы на силу тяжести тела и силу давления вытесняемой жидкости. Удобнее сначала вычислить их по отдельности, а затем рассмотреть тело, на которое действуют две силы – сила тяжести тела, определяемая по формулам (4) - (6), и выталкивающая сила, которая вычисляется по тем же формулам, только направлена вверх, и под массой подразумевается масса жидкости, вытесняемой телом.
Координаты центра тяжести сплошных тел в пространстве
В большинстве случаев твердые тела являются сплошными, заполняющими некоторый объем V. Тогда для расчета центра тяжести нужно от суммирования перейти к интегрированию. Для этого разделим тело на большое число частей, каждую из которых можно считать материальной точкой, занимающей объем с массой , где – плотность части тела. Далее выполняем предельный переход . В результате бесконечно малые величины заменятся дифференциалами, а операция суммирования – интегрированием; плотность будет функцией от координат. Преобразуем (4) - (6):
:
;
;
.
В результате мы получили формулы для вычисления координат центра тяжести сплошного неоднородного тела, зная распределение его плотности :
(7) ;
(8) ;
(9) .
Интегрирование ведется по объему, занимаемого телом. Элемент объема является произведением дифференциалов координат: . Каждый интеграл является трехкратным. То есть, для их вычисления нужно сначала проинтегрировать по , затем по и , или в другом более удобном порядке. Также можно применять другие приемы вычисления тройных интегралов.
Отметим полезные формулы, полученные выше, в которых интегралы выражаются через массы dm элементарных объемов dV, на которые делится тело при переходе от суммирования к интегрированию.
(10) ;
(11) .
Однородные тела
Для однородных тел плотность постоянна, и, при вычислении координат центра тяжести, она сокращается: . Тогда
(12) ;
(13) ;
(14) .
Здесь – элементарный элемент объема тела.
Плоская фигура
Плоские фигуры используются для описания свойств, как листовых материалов, так и различных профилей, имеющих постоянное сечение. Плоскую фигуру можно рассматривать, как объемное тело, размеры которого по одной из координат стремятся к нулю. В качестве такой координаты, как правило, используют z. То есть считают, что по оси z тело расположено при , где , а сама фигура расположена в плоскости xy. Для плоской фигуры плотность определяется как отношение массы dm к площади dA элемента: .
Рассмотрим плоскую неоднородную фигуру. Для нее плотность является функцией от x, y: . Выразим массу dm элемента площади dA = dxdy фигуры через плотность: . Подставляя в (10) и (11), получим формулы координат центра тяжести плоской неоднородной фигуры.
(15) ;
(16) ;
(17) .
Интегрирование ведется по площади, занимаемой телом. Элемент площади является произведением дифференциалов координат: . Каждый интеграл является двукратным.
Рассмотрим плоскую однородную фигуру. Для нее плотность постоянна: . Подставив в предыдущие формулы ее постоянное значение, получим формулы координат центра тяжести плоской однородной фигуры.
(18) ;
(19) ;
(20) .
Здесь – бесконечно малый элемент площади фигуры.
Линейное тело
Наконец рассмотрим линейное тело, у которого размеры в двух направлениях пренебрежимо малы. К таким телам относятся стержневые и проволочные конструкции, которые могут быть изогнуты. В таких телах элемент массы dm пропорционален элементу длины dl: , где – линейная плотность, которую будем считать постоянной. Тогда – это масса единицы длины тела. Подставляя в (10) и (11), получим формулы координат центра тяжести линейного тела.
(21) ;
(22) ;
(23) .
Здесь – длина тела, полученная разбиением его на большое число бесконечно малых элементов, и суммированием длин всех элементов. Интегрирование удобно выполнять в параметрическом виде. Для этого нужно выразить координаты точек тела через параметр, который обозначим как :
.
Пусть параметр принимает значения . Тогда интегрирование по элементам длины сводится к интегрированию по параметру от до . При этом элемент нужно выразить через дифференциал :
.
Статический момент
Входящую в (2) сумму называют статическим моментом системы параллельных сил относительно точки O:
.
Это векторная величина. Однако, в различных приложениях используют ее компоненты, которые соотносят не с направлениями осей, а с плоскостями системы координат.
- Статическими моментами системы параллельных сил относительно координатных плоскостей
- называют алгебраические величины
.
Здесь – модуль силы, приложенной в точке с координатами . Все силы считаются параллельными.
Наибольшее применение статические моменты получили для плоской однородной фигуры. В этом случае их определяют на основании формул (20).
- Статические моменты площади
- Выражения
называются статическими моментами площади относительно осей x и y. Они измеряются в см3.
Если положение центра тяжести сечения известно , то статический момент равен произведению площади фигуры A на алгебраическое расстояние от центра тяжести до соответствующей оси:
.
Автор: Олег Одинцов. Опубликовано:
