Все картинки раздела «Статика»
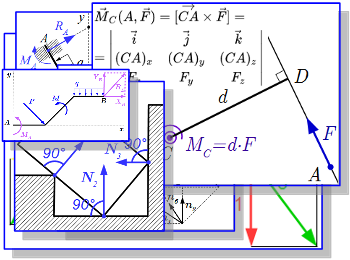
Здесь собраны все изображения раздела «Статика» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением.
Содержание
См. также:
Все понятия, определения и теоремы статики (обзорная страница)
Статика – все понятия, определения, законы и теоремы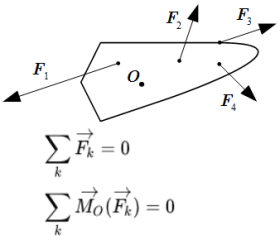
Все понятия и законы статики на одной странице, включая определения, аксиомы, теоремы и свойства. 
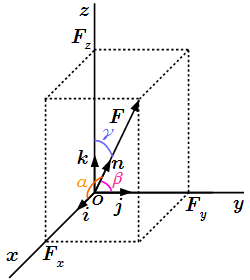Вектор силы F и ее проекции на оси пространственной системы координат. 
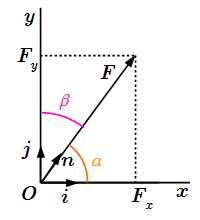Вектор силы F и ее проекции на оси плоской системы координат. 
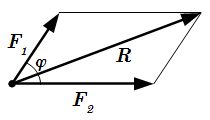Сложение сил по правилу параллелограмма 
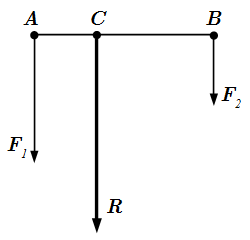Две параллельные силы F1 и F2 имеют равнодействующую R. 
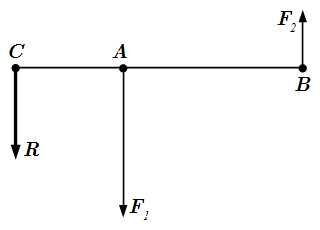Две не равные противоположно направленные силы F1 и F2 имеют равнодействующую R. 
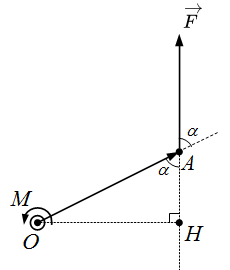Момент силы равен произведению силы F на плечо OH. 
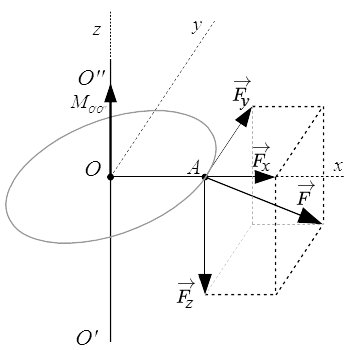Момент силы относительно оси. 
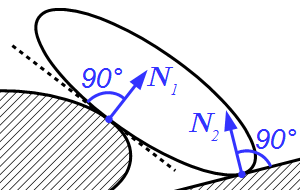Реакции на гладких поверхностях 
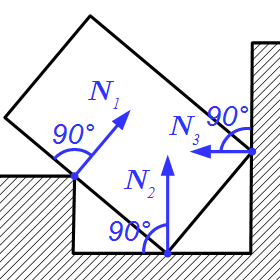Реакции на поверхностях с острием 
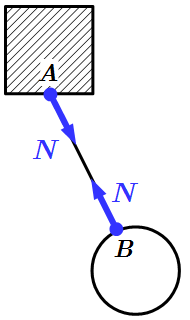Реакция нити 
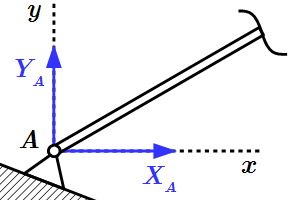Неподвижный шарнир 
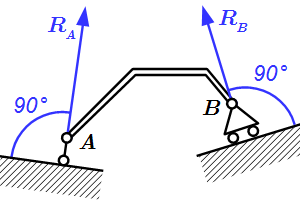Подвижный шарнир 
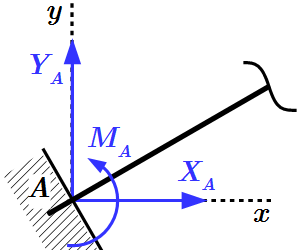Заделка 
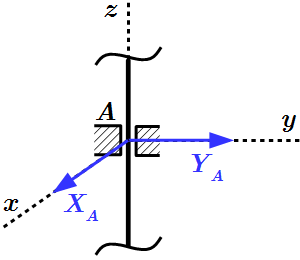Цилиндрический шарнир 
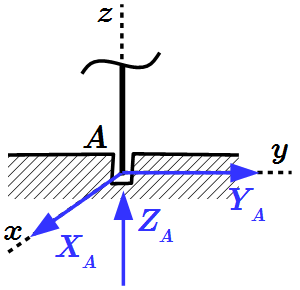Подпятник 
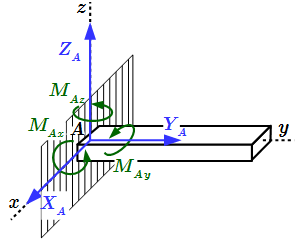Заделка в пространстве 
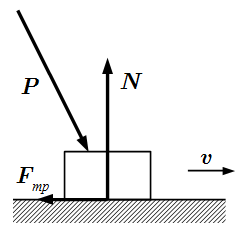Сила трения скольжения Fтр = f·N. 
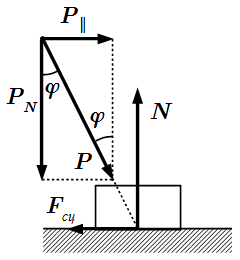Сила трения сцепления. Движение возможно при tg φ > f0. 
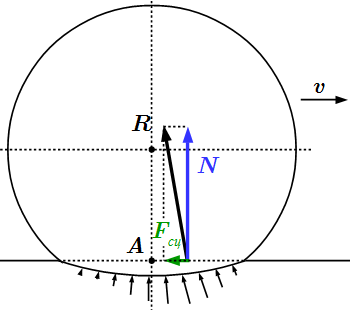Силы, возникающие при деформации, препятствуют качению тела круглой формы по плоской поверхности. 
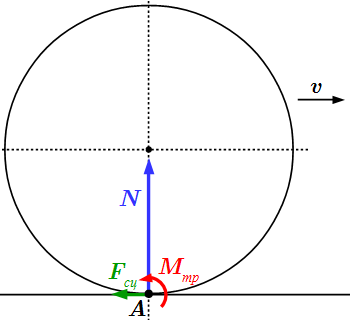Расчетная схема трения качения. 
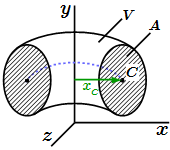Объем тела вращения 
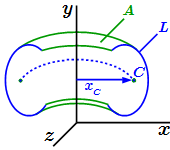Площадь тела вращения 
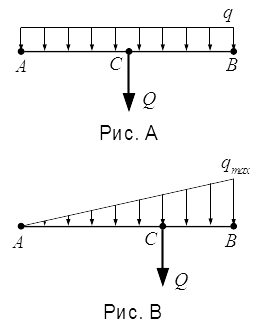Равномерно (А) и линейно (Б) распределенная нагрузка. 
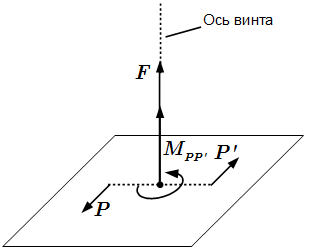Динама – одна из простейших систем сил.
Все понятия и законы статики на одной странице, включая определения, аксиомы, теоремы и свойства. Вектор силы F и ее проекции на оси пространственной системы координат. Вектор силы F и ее проекции на оси плоской системы координат. Сложение сил по правилу параллелограмма Две параллельные силы F1 и F2 имеют равнодействующую R. 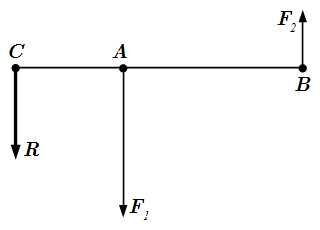Две не равные противоположно направленные силы F1 и F2 имеют равнодействующую R. Момент силы равен произведению силы F на плечо OH. Момент силы относительно оси. Реакции на гладких поверхностях Реакции на поверхностях с острием Реакция нити Неподвижный шарнир Подвижный шарнир Заделка Цилиндрический шарнир Подпятник Заделка в пространстве Сила трения скольжения Fтр = f·N. Сила трения сцепления. Движение возможно при tg φ > f0. Силы, возникающие при деформации, препятствуют качению тела круглой формы по плоской поверхности. Расчетная схема трения качения. Объем тела вращения Площадь тела вращения Равномерно (А) и линейно (Б) распределенная нагрузка. Динама – одна из простейших систем сил. Другие страницы
Основные понятия и определения статики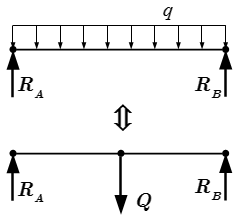
Изложены основные понятия и определения статики – раздела теоретической механики. Рассмотрена основная задача статики и область ее применения. Даны определения, связанные с системами тел, кинематическим состоянием тела и действующими силами. 
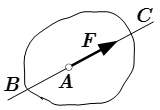Линия действия силы Силы в теоретической механике
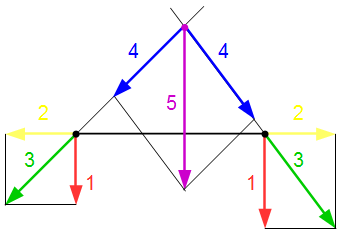Дано определение силы, действующей на материальную точку. Показано, что в теоретической механике, в задачах на определение движения твердых тел, силы являются скользящими векторами. Поэтому системы сил можно преобразовывать в более простые эквивалентные системы. Показано, что получить эквивалентную систему, можно решая задачу статики, в которой к старой системе добавляется новая система сил. Аксиомы статики
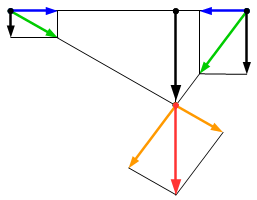Изложены аксиомы статики. Пояснена их роль в теоретической механике. Приводится пример графического решения задачи, применяя только аксиомы статики. Сложение сил по правилу параллелограмма. 
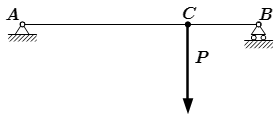Рис 1. Условие задачи. 
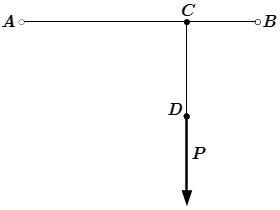Рис 2. Перемещение силы P. 
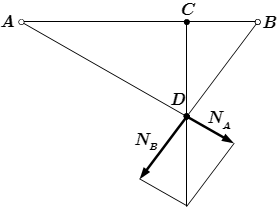Рис 3. Разложение силы P по правилу параллелограмма. 
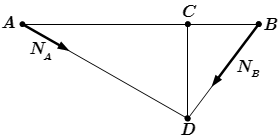Рис 4. Перемещение точек приложения сил. 
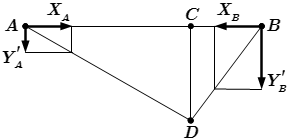Рис 5. Разложение сил на горизонтальные и вертикальные составляющие. 
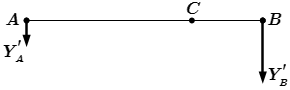Рис 6. Система, эквивалентная одной силе P, приложенной в точке C. 
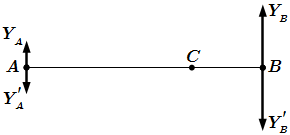Рис 7. Уравновешенная система сил. 
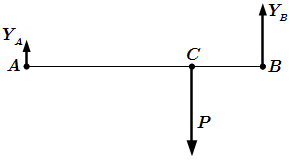Рис 8. Решение задачи. 
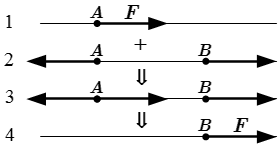Сила в статике – скользящий вектор Определение и свойства момента силы
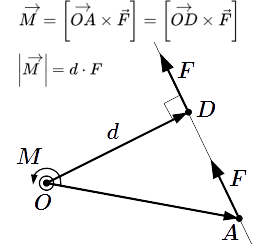Определения и свойства момента силы относительно точки и оси. Определение плеча силы. Выражение абсолютного значения момента в виде произведения плеча на модуль силы. 
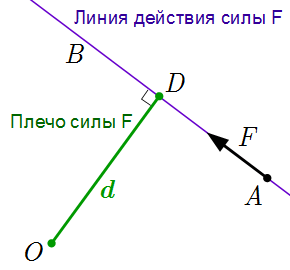Плечо силы F 
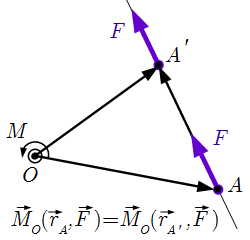Перемещение точки приложения силы вдоль ее линии действия. 
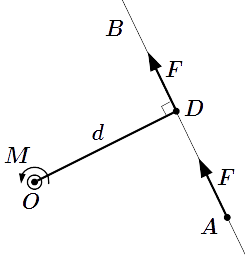Абсолютное значение момента M относительно точки O равно произведению силы F на ее плечо d = |OD|. Способы расчета момента силы относительно точки и оси
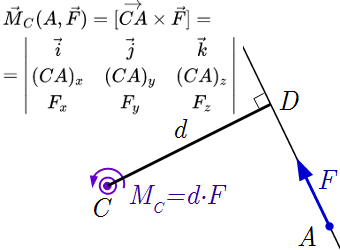Рассмотрены способы определения момента силы относительно точки и оси. Приедены примеры расчетов. 
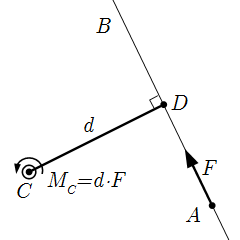Вектор момента M перпендикулярен плоскости рисунка и направлен на нас. 
Для определения проекций вектора силы на оси координат, мы строим новую систему координат с началом в точке приложения A силы F.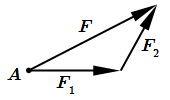 
Неправильное разложение силы по правилу параллелограмма 
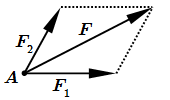Правильное разложение силы по правилу параллелограмма 
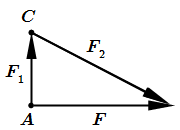Неправильное разложение силы по правилу параллелограмма может привести к ошибке 
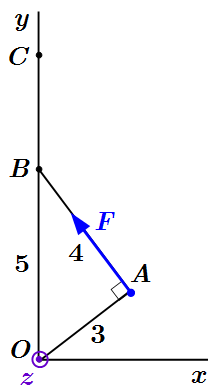В плоской задаче момент имеет только одну проекцию на воображаемую ось Oz, перпендикулярную плоскости фигуры. 
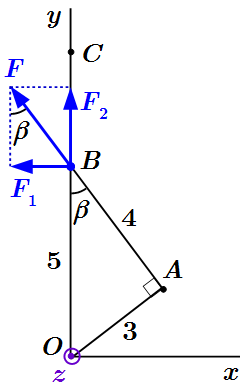Сила F, перемещенная вдоль линии действия и разложенная по правилу параллелограмма. 
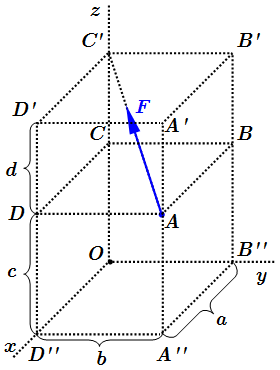Сила F, приложенная к вершине прямоугольного параллелепипеда ABCDA'B'C'D'. 
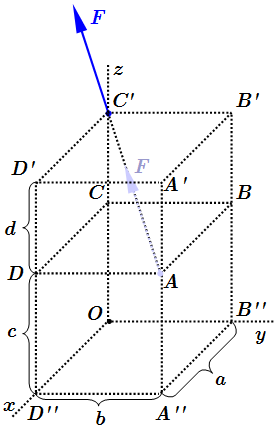Перемещение силы F, вдоль ее линии действия. Условия равновесия твердого тела и системы сил
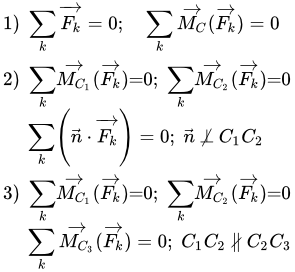Обсуждается связь между понятиями "равновесие твердого тела" и "равновесие системы сил". Приводятся три формы условий равновесия твердого тела, как для пространственной системы сил, так и для плоской. Дано доказательство всех форм условий равновесия. Равнодействующая системы двух параллельных сил
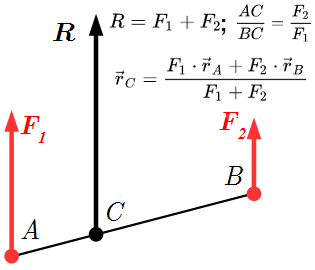Расчет равнодействующей системы двух параллельных сил тремя способами, используя аксиомы статики и уравнения равновесия. 
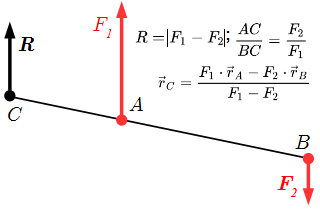Две не равные противоположно направленные силы F1 и F2 имеют равнодействующую R. 
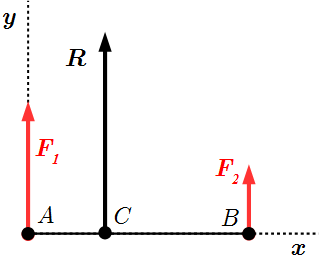Сонаправленные силы и их равнодействующая. 
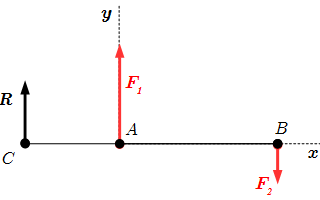Противоположно направленные силы и их равнодействующая. 
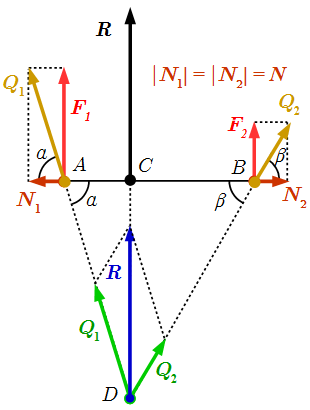Преобразование двух сонаправленных сил. 
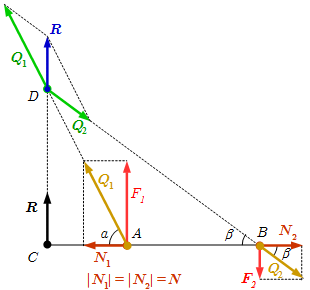Преобразование двух противоположно направленных сил. Центр системы параллельных сил
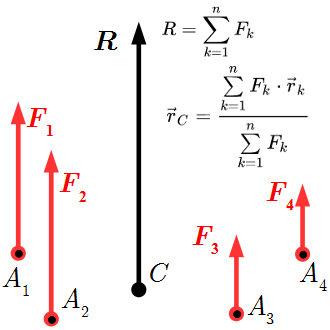Определение центра параллельных сил. Доказано двумя способами, что система сил, параллельных некоторой оси, векторная сумма которых не равна нулю, имеет равнодействующую, проходящую через центр параллельных сил. Две сонаправленные параллельные силы F1 и F2 имеют равнодействующую R. Две не равные противоположно направленные силы F1 и F2 имеют равнодействующую R. Понятие и формулы координат центра тяжести тела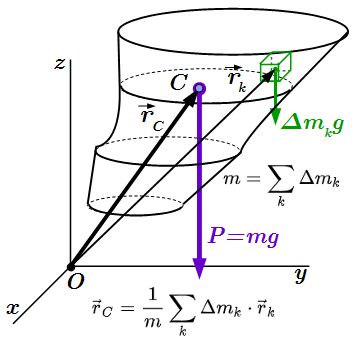
Понятие центра тяжести тела. Формулы расчета координат центра тяжести для неоднородного и однородного сплошного тела, а также для плоской фигуры. Статический момент. Аксиома связей (принцип освобождаемости от связей)
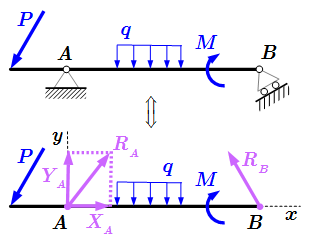Формулировка принципа освобождаемости от связей, который часто называется аксиомой связей. Показано, что аксиома связей является следствием основных законов механики. Даны определения активных и пассивных сил. Рассмотрено применение принципа освобождаемости от связей для решения механических задач, в которых тела соединены друг с другом и с неподвижным основанием. Примеры приведения таких задач к задаче со свободными телами. 
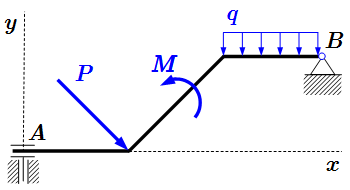Ломаный брус со связями. 
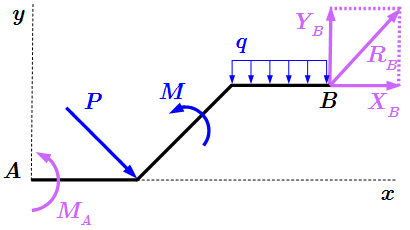Освобождение от связей в ломаном брусе. 
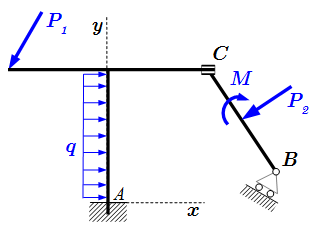Составная конструкция со связями. 
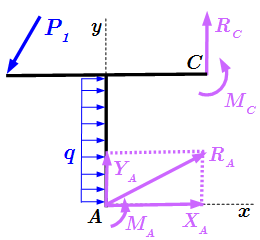Освобождение от связей в раме. 
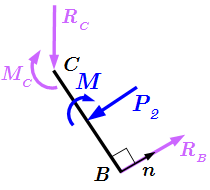Освобождение от связей в стержне. 
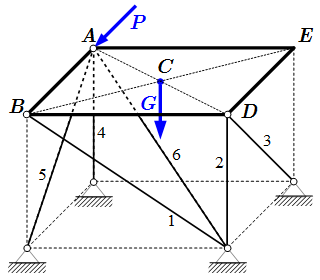Плита со связями. 
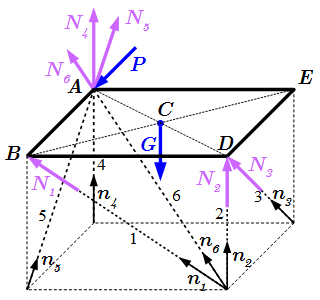Освобождение от связей в плите. Основные типы связей и их реакции, применяемые в технической механике
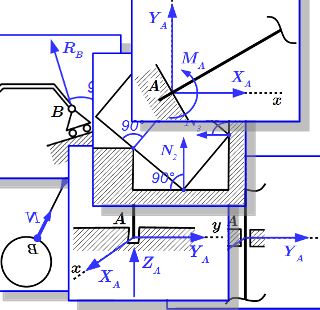Приводятся основные виды связей и их реакции, применяемые в технической механике при проектировании машин и механизмов. Даны их условные обозначения и направления сил реакций. Реакции на гладких поверхностях Реакции на поверхностях с острием Реакция нити 
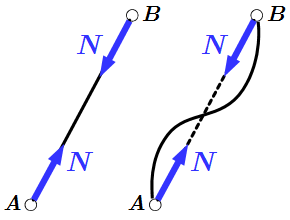Реакции невесомого стержня Неподвижный шарнир Подвижный шарнир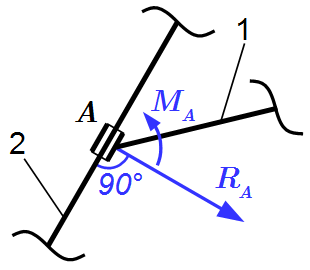 
Ползун на стержне 
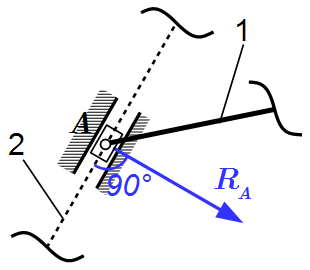Ползун в направляющих Заделка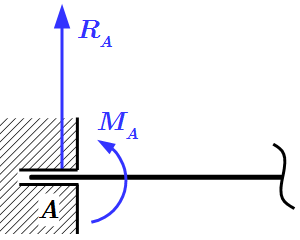 
Скользящая заделка 
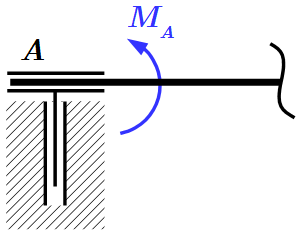Бискользящая заделка Цилиндрический шарнир Подпятник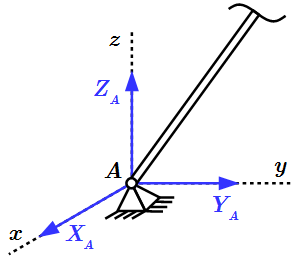 
Сферический (шаровой) шарнир Заделка в пространстве Методы определения реакций опор твердого тела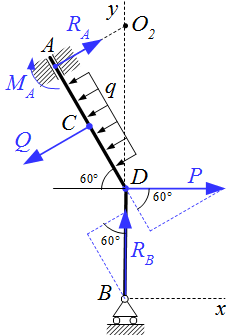
Рассмотрены методы определения реакций опор твердого тела для статически определимых схем закреплений тел в опорах. Определение реакций опор твердого тела – решение задачи
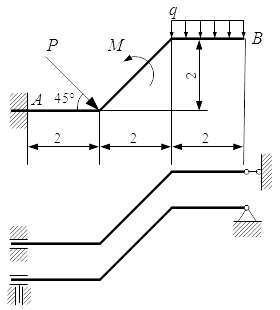Приводится решение задачи, в которой требуемая реакция опоры твердого тела определяется из одного уравнения, без определения остальных сил реакций. Для трех вариантов закрепления тела выбирается тот, при котором требуемая реакция имеет наименьшее значение. Для этого варианта определяются реакции остальных опор. 
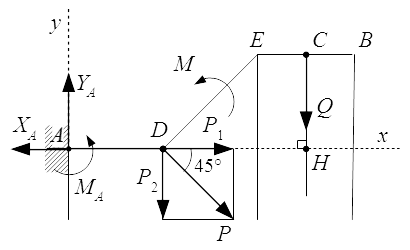Реакции опор для схемы №1. 
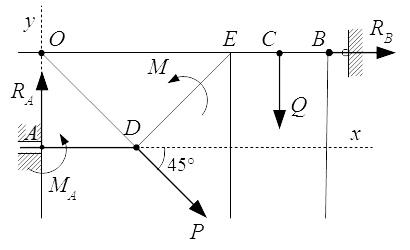Реакции опор для схемы №2. 
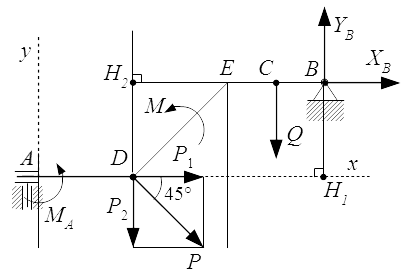Реакции опор для схемы №3. Определение реакций опор балки – решение задачи
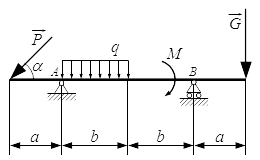Рассмотрен порядок решения задач на определение реакций опор балок. Приводится пример решения задачи двумя способами и проверка правильности определения реакций. 
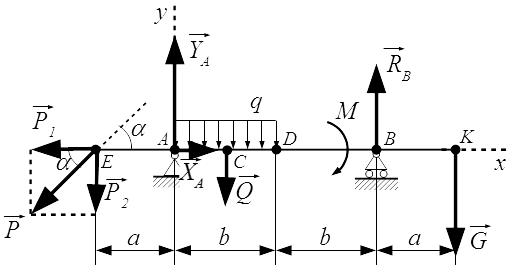Силы, действующие на балку. Определение реакций опор составной конструкции – решение задачи
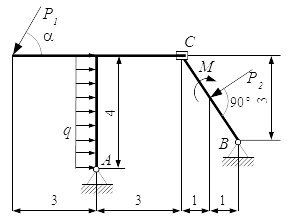Рассмотрен метод решения задач на определение реакций опор составных конструкций для статически определимых систем. Приводится пример решения задачи, в которой требуется определить реакции в опорах и в точке соединения частей составной конструкции. 
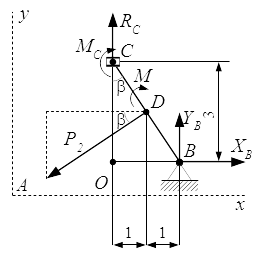Реакции опор, поддерживающие равновесие правой части конструкции. 
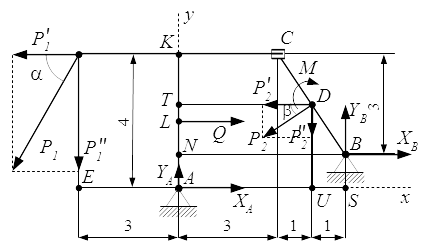Реакции опор, поддерживающие равновесие всей конструкции. 
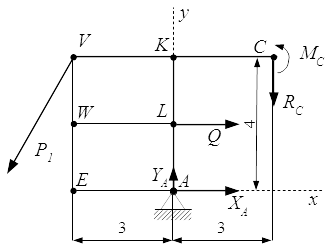Реакции опор, поддерживающие равновесие левой части конструкции. Определение реакций стержней, поддерживающих прямоугольную плиту – решение задачи
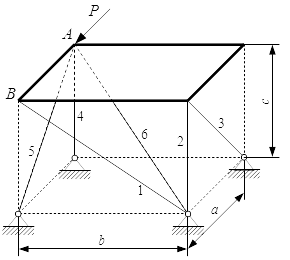Рассмотрены методы решения задач на равновесие с произвольной пространственной системой сил. Приводится пример решения задачи на равновесие плиты, поддерживаемой стержнями в трехмерном пространстве. Показано, как за счет выбора осей при составлении уравнений равновесия, можно упростить решение задачи. 
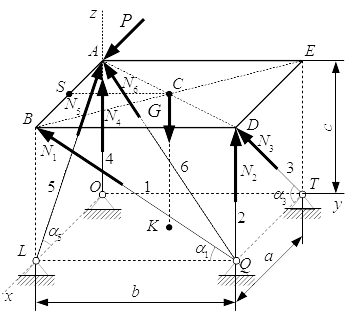Силы, поддерживающие равновесие плиты в трехмерном пространстве.
Изложены основные понятия и определения статики – раздела теоретической механики. Рассмотрена основная задача статики и область ее применения. Даны определения, связанные с системами тел, кинематическим состоянием тела и действующими силами. Линия действия силы Силы в теоретической механикеДано определение силы, действующей на материальную точку. Показано, что в теоретической механике, в задачах на определение движения твердых тел, силы являются скользящими векторами. Поэтому системы сил можно преобразовывать в более простые эквивалентные системы. Показано, что получить эквивалентную систему, можно решая задачу статики, в которой к старой системе добавляется новая система сил. Аксиомы статикиИзложены аксиомы статики. Пояснена их роль в теоретической механике. Приводится пример графического решения задачи, применяя только аксиомы статики. Сложение сил по правилу параллелограмма. Рис 1. Условие задачи. Рис 2. Перемещение силы P. Рис 3. Разложение силы P по правилу параллелограмма. Рис 4. Перемещение точек приложения сил. Рис 5. Разложение сил на горизонтальные и вертикальные составляющие. Рис 6. Система, эквивалентная одной силе P, приложенной в точке C. 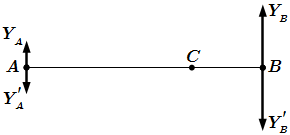Рис 7. Уравновешенная система сил. Рис 8. Решение задачи. Сила в статике – скользящий вектор Определение и свойства момента силыОпределения и свойства момента силы относительно точки и оси. Определение плеча силы. Выражение абсолютного значения момента в виде произведения плеча на модуль силы. Плечо силы F Перемещение точки приложения силы вдоль ее линии действия. Абсолютное значение момента M относительно точки O равно произведению силы F на ее плечо d = |OD|. Способы расчета момента силы относительно точки и осиРассмотрены способы определения момента силы относительно точки и оси. Приедены примеры расчетов. Вектор момента M перпендикулярен плоскости рисунка и направлен на нас. Для определения проекций вектора силы на оси координат, мы строим новую систему координат с началом в точке приложения A силы F. Неправильное разложение силы по правилу параллелограмма Правильное разложение силы по правилу параллелограмма Неправильное разложение силы по правилу параллелограмма может привести к ошибке В плоской задаче момент имеет только одну проекцию на воображаемую ось Oz, перпендикулярную плоскости фигуры. Сила F, перемещенная вдоль линии действия и разложенная по правилу параллелограмма. Сила F, приложенная к вершине прямоугольного параллелепипеда ABCDA'B'C'D'. Перемещение силы F, вдоль ее линии действия. Условия равновесия твердого тела и системы сил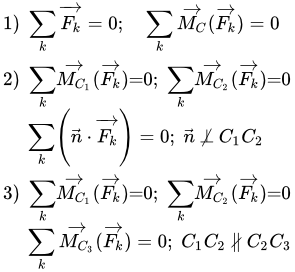Обсуждается связь между понятиями "равновесие твердого тела" и "равновесие системы сил". Приводятся три формы условий равновесия твердого тела, как для пространственной системы сил, так и для плоской. Дано доказательство всех форм условий равновесия. Равнодействующая системы двух параллельных силРасчет равнодействующей системы двух параллельных сил тремя способами, используя аксиомы статики и уравнения равновесия. Две не равные противоположно направленные силы F1 и F2 имеют равнодействующую R. Сонаправленные силы и их равнодействующая. Противоположно направленные силы и их равнодействующая. Преобразование двух сонаправленных сил. Преобразование двух противоположно направленных сил. Центр системы параллельных силОпределение центра параллельных сил. Доказано двумя способами, что система сил, параллельных некоторой оси, векторная сумма которых не равна нулю, имеет равнодействующую, проходящую через центр параллельных сил. Две сонаправленные параллельные силы F1 и F2 имеют равнодействующую R. Две не равные противоположно направленные силы F1 и F2 имеют равнодействующую R. Понятие и формулы координат центра тяжести телаПонятие центра тяжести тела. Формулы расчета координат центра тяжести для неоднородного и однородного сплошного тела, а также для плоской фигуры. Статический момент. Аксиома связей (принцип освобождаемости от связей)Формулировка принципа освобождаемости от связей, который часто называется аксиомой связей. Показано, что аксиома связей является следствием основных законов механики. Даны определения активных и пассивных сил. Рассмотрено применение принципа освобождаемости от связей для решения механических задач, в которых тела соединены друг с другом и с неподвижным основанием. Примеры приведения таких задач к задаче со свободными телами. Ломаный брус со связями. Освобождение от связей в ломаном брусе. Составная конструкция со связями. Освобождение от связей в раме. Освобождение от связей в стержне. Плита со связями. Освобождение от связей в плите. Основные типы связей и их реакции, применяемые в технической механикеПриводятся основные виды связей и их реакции, применяемые в технической механике при проектировании машин и механизмов. Даны их условные обозначения и направления сил реакций. Реакции на гладких поверхностях Реакции на поверхностях с острием Реакция нити Реакции невесомого стержня Неподвижный шарнир Подвижный шарнир Ползун на стержне Ползун в направляющих Заделка Скользящая заделка Бискользящая заделка Цилиндрический шарнир Подпятник Сферический (шаровой) шарнир Заделка в пространстве Методы определения реакций опор твердого телаРассмотрены методы определения реакций опор твердого тела для статически определимых схем закреплений тел в опорах. Определение реакций опор твердого тела – решение задачиПриводится решение задачи, в которой требуемая реакция опоры твердого тела определяется из одного уравнения, без определения остальных сил реакций. Для трех вариантов закрепления тела выбирается тот, при котором требуемая реакция имеет наименьшее значение. Для этого варианта определяются реакции остальных опор. Реакции опор для схемы №1. Реакции опор для схемы №2. Реакции опор для схемы №3. Определение реакций опор балки – решение задачиРассмотрен порядок решения задач на определение реакций опор балок. Приводится пример решения задачи двумя способами и проверка правильности определения реакций. Силы, действующие на балку. Определение реакций опор составной конструкции – решение задачиРассмотрен метод решения задач на определение реакций опор составных конструкций для статически определимых систем. Приводится пример решения задачи, в которой требуется определить реакции в опорах и в точке соединения частей составной конструкции. Реакции опор, поддерживающие равновесие правой части конструкции. Реакции опор, поддерживающие равновесие всей конструкции. Реакции опор, поддерживающие равновесие левой части конструкции. Определение реакций стержней, поддерживающих прямоугольную плиту – решение задачиРассмотрены методы решения задач на равновесие с произвольной пространственной системой сил. Приводится пример решения задачи на равновесие плиты, поддерживаемой стержнями в трехмерном пространстве. Показано, как за счет выбора осей при составлении уравнений равновесия, можно упростить решение задачи. Силы, поддерживающие равновесие плиты в трехмерном пространстве. ❮ Задачи с решениями | Кинематика в картинках
См. также: