Теорема Больцано – Вейерштрасса
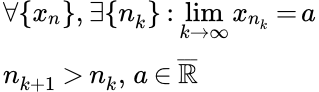
Теорема Больцано – Вейерштрасса
Из любой ограниченной последовательности действительных чисел можно выделить подпоследовательность, сходящуюся к конечному числу. А из любой неограниченной последовательности – бесконечно большую подпоследовательность, сходящуюся к или к .
Теорему Больцано – Вейерштрасса можно сформулировать и так.
Из любой последовательности действительных чисел можно выделить подпоследовательность, сходящуюся или к конечному числу, или к или к .
Доказательство первой части теоремы
Для доказательства первой части теоремы мы применим лемму о вложенных отрезках.
Пусть последовательность ограничена. Это означает, что существует положительное число M, так что для всех n,
.
То есть все члены последовательности принадлежат отрезку , который мы обозначим как . Здесь . Длина первого отрезка . В качестве первого элемента подпоследовательности возьмем любой элемент последовательности . Обозначим его как .
Разделим отрезок пополам. Если в его правой половине содержится бесконечное число элементов последовательности , то следующим отрезком возьмем правую половину . В противном случае возьмем левую половину. В результате мы получим второй отрезок , содержащий бесконечное число элементов последовательности. Длина этого отрезка . Здесь , если мы взяли правую половину ; и – если левую. В качестве второго элемента подпоследовательности возьмем любой элемент последовательности, принадлежащий второму отрезку с номером большим, чем n1. Обозначим его как ().
Этим способом повторяем процесс деления отрезков. Делим отрезок пополам. Если в его правой половине содержится бесконечное число элементов последовательности, то следующим отрезком возьмем правую половину . В противном случае возьмем левую половину. В результате мы получим отрезок , содержащий бесконечное число элементов последовательности. Длина этого отрезка . В качестве элемента подпоследовательности возьмем любой элемент последовательности, принадлежащий отрезку с номером большим чем nk.
В результате мы получаем подпоследовательность и систему вложенных отрезков
.
Причем каждый элемент подпоследовательности принадлежит соответствующему отрезку:
.
Поскольку длины отрезков , при , стремятся к нулю, то согласно лемме о вложенных отрезках, существует единственная точка c, принадлежащая всем отрезкам.
Покажем, что эта точка является пределом подпоследовательности:
.
Действительно, поскольку точки и c принадлежат отрезку длины , то
.
Поскольку , то согласно теореме о промежуточных последовательностях,
. Отсюда
.
Первая часть теоремы доказана.
Доказательство второй части теоремы
Пусть последовательность неограниченна. Это означает, что для любого числа M, существует такое n, что
.
Сначала рассмотрим случай, когда последовательность неограниченна справа. То есть для любого M > 0, существует такое n, что
.
В качестве первого элемента подпоследовательности возьмем любой элемент последовательности , больший единицы:
.
В качестве второго элемента подпоследовательности возьмем любой элемент последовательности, больший двойки:
,
и чтобы .
И так далее. В качестве k-го элемента подпоследовательности возьмем любой элемент
,
причем .
В результате получим подпоследовательность, каждый элемент которой удовлетворяет неравенству:
.
Вводим числа M и NM, связав их соотношениями:
.
Отсюда следует, что для любого числа M можно подобрать натуральное число , так что для всех натуральных k > NM выполняется неравенство .
Это означает, что
.
Теперь рассмотрим случай, когда последовательность ограничена справа. Поскольку она неограниченна, то она должна быть неограниченной слева. В этом случае повторяем рассуждения с небольшими поправками.
Выбираем подпоследовательность, чтобы ее элементы удовлетворяли неравенствам:
.
Затем вводим числа M и NM, связав их соотношениями:
.
Тогда для любого числа M можно подобрать натуральное число , так что для всех натуральных k > NM выполняется неравенство .
Это означает, что
.
Теорема доказана.
Автор: Олег Одинцов. Опубликовано:
