Свойства бесконечно больших последовательностей
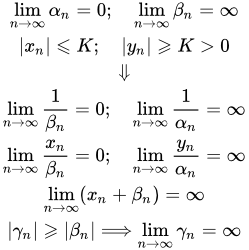
Формулировки свойств
Связь между бесконечно большой и бесконечно малой последовательностью
Если последовательность {βn} является бесконечно большой, то, начиная с некоторого номера N, определена последовательность {1/βn}, которая является бесконечно малой. Если {αn} является бесконечно малой последовательностью, с отличными от нуля членами, то последовательность {1/αn} является бесконечно большой.
Доказательство ⇓
Сумма бесконечно большой и ограниченной последовательности
Сумма или разность бесконечно большой и ограниченной последовательности является бесконечно большой последовательностью:
,
где .
Доказательство ⇓
Произведение бесконечно большой и ограниченной снизу последовательности
Если абсолютные значения элементов последовательности {yn} ограничены снизу положительным числом ( |yn| ≥ K > 0), а {βn} – бесконечно большая последовательность: , то их произведение является бесконечно большой последовательностью:
.
Доказательство ⇓
Частное ограниченной и бесконечно большой последовательности
Если последовательность {βn} бесконечно большая, с неравными нулю членами, а последовательность {xn} ограничена, то
.
Доказательство ⇓
Частное ограниченной снизу и бесконечно малой последовательностью
Если абсолютные значения элементов последовательности {yn} ограничены снизу положительным числом ( |yn| ≥ K > 0), а {αn} – бесконечно малая с неравными нулю членами, то
.
Доказательство ⇓
Свойство неравенств бесконечно больших последовательностей
Пусть последовательность бесконечно большая. И пусть элементы последовательности , начиная с некоторого номера, удовлетворяют неравенствам:
.
Тогда последовательность также бесконечно большая.
Доказательство ⇓
Это свойство имеет два частных случая, которые доказываются аналогичным способом.
Пусть элементы последовательностей и , начиная с некоторого номера, удовлетворяют неравенствам:
.
Тогда, если последовательность сходится к : ,
то и последовательность сходится к : .
Если последовательность сходится к : ,
то и последовательность сходится к : .
Арифметические свойства бесконечно больших и бесконечно малых последовательностей
Приведенные выше свойства выполняются, если последовательность ограничена, а последовательность абсолютных членов ограничена снизу положительным числом. При этом эти последовательности не обязательно должны иметь конечный предел, а могут расходиться. Однако, эти последовательности будут обладать указанными свойствами, если они имеют соответствующие пределы. Это позволяет сформулировать арифметические свойства бесконечно больших и бесконечно малых последовательностей.
Пусть существуют пределы и числовых последовательностей и . Причем . И пусть последовательность бесконечно малая: , а последовательность бесконечно большая: .
Тогда существует пределы суммы и разности:
;
существуют пределы произведений:
;
существуют пределы частного:
при ,
при .
Действительно, если последовательность сходится к конечному числу, то она ограничена (см. «Теорема об ограниченности последовательности, имеющей конечный предел»).
Если последовательность сходится к конечному числу b, отличному от нуля, то . Тогда, начиная с некоторого номера, (см. «Теорема о последовательностях, пределы которых связаны неравенством»). Конечное число членов мы можем отбросить. Это никак не влияет на сходимость (см. «Влияние конечного числа элементов на сходимость»).
Таким образом, при указанных значениях пределов последовательностей и , выполняются условия, применяемые при доказательстве приведенных выше свойств.
Доказательство свойств
Связь между бесконечно большой и бесконечно малой последовательностью
Все свойства ⇑ Если последовательность {βn} является бесконечно большой, то, начиная с некоторого номера N, определена последовательность {1/βn}, которая является бесконечно малой. Если {αn} является бесконечно малой последовательностью, с отличными от нуля членами, то последовательность {1/αn} является бесконечно большой.
Доказательство
Пусть последовательность являются бесконечно большой. Это означает, что имеется некоторая функция , так что для любого положительного числа M выполняется неравенство:
(1.1) при .
Подставим сюда :
.
Это означает, что начиная с номера , члены последовательности имеют отличные от нуля значения и поэтому определена последовательность .
Умножим первое неравенство (1.1) на положительное число :
.
Тогда вместо (1.1) имеем:
.
Введем положительное число . Тогда любому положительному значению переменной соответствует положительное значение переменной . И предыдущее неравенство приобретает вид:
при .
Итак, мы нашли такую функцию , при которой для любого положительного числа выполняется неравенство:
при .
Это означает, что предел последовательности равен нулю. То есть она является бесконечно малой последовательностью.
Первая часть свойства доказана.
Докажем вторую часть. Пусть последовательность являются бесконечно малой с отличными от нуля членами, . Это означает, что имеется некоторая функция , так что для любого положительного числа ε выполняется неравенство:
(1.2) при .
Умножим первое неравенство (1.2) на положительное число :
.
Тогда вместо (1.2) имеем:
.
Подставим :
.
Итак, мы нашли такую функцию , при которой для любого положительного числа выполняется неравенство:
при .
Это означает, что последовательность является бесконечно большой.
Свойство доказано.
Сумма бесконечно большой и ограниченной последовательности
Все свойства ⇑ Сумма или разность бесконечно большой и ограниченной последовательности является бесконечно большой последовательностью:
,
где .
Доказательство
Пусть члены последовательности ограничены, по абсолютной величине положительным числом:
(2.1) .
Пусть последовательность являются бесконечно большой. Это означает, что имеется некоторая функция , так что для любого положительного числа M1 выполняется неравенство:
(2.2) при .
Нам нужно показать, что имеется некоторая функция , так что для любого положительного числа M выполняется неравенство:
(2.3) при .
Подставим в (2.2) :
.
Это означает, что
(2.4) при .
Сделаем оценку для . При этом мы воспользуемся свойствами неравенств и применим (2.1), (2.2) и (2.4):
.
Эти неравенства выполняются при и . Введем число . Тогда
при ,
где
.
То есть мы нашли такую функцию , при которой для любого выполняется (4.3).
Свойство доказано.
Произведение бесконечно большой и ограниченной снизу последовательности
Все свойства ⇑ Если абсолютные значения элементов последовательности {yn} ограничены снизу положительным числом ( |yn| ≥ K > 0), а {βn} – бесконечно большая последовательность: , то их произведение является бесконечно большой последовательностью:
.
Доказательство
Поскольку последовательность являются бесконечно большой, то имеется некоторая функция , так что для любого положительного числа выполняется неравенство:
(3.1) при .
Согласно определению бесконечно большой последовательности, нам нужно найти такую функцию , так что для любого положительного числа M > 0 выполняется неравенство:
(3.2) при .
Сделаем оценку произведения . Подставим и . При имеем:
.
Введем положительное число . Любому положительному M соответствует положительное . Подставим :
.
Сравнивая с (3.2) мы видим, что нашли такую функцию , при которой для любого положительного числа выполняется (3.2).
Свойство доказано.
Частное ограниченной и бесконечно большой последовательности
Все свойства ⇑ Если последовательность {βn} бесконечно большая, с неравными нулю членами, а последовательность {xn} ограничена, то
.
Доказательство
Поскольку последовательность является бесконечно большой, то, согласно свойству 1, последовательность с членами является бесконечно малой. Но произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью. См. «Произведение ограниченной последовательности на бесконечно малую». Поэтому
.
Свойство доказано.
Частное ограниченной снизу и бесконечно малой последовательностью
Все свойства ⇑ Если абсолютные значения элементов последовательности {yn} ограничены снизу положительным числом ( |yn| ≥ K > 0), а {αn} – бесконечно малая с неравными нулю членами, то
.
Доказательство
Поскольку последовательность являются бесконечно малой, то имеется некоторая функция , так что для любого положительного числа ε выполняется неравенство:
(5.1) при .
Согласно определению бесконечно большой последовательности, нам нужно найти такую функцию , так что для любого положительного числа M > 0 выполняется неравенство:
(5.2) при .
Сделаем оценку для дроби . Подставим и . При имеем:
.
Введем положительное число . Любому положительному M соответствует положительное ε. Подставим :
.
Сравнивая с (5.2) мы видим, что нашли такую функцию , при которой для любого положительного числа выполняется (5.2).
Свойство доказано.
Свойство неравенств бесконечно больших последовательностей
Все свойства ⇑ Пусть последовательность бесконечно большая. И пусть элементы последовательности , начиная с некоторого номера, удовлетворяют неравенствам:
.
Тогда последовательность также бесконечно большая.
Доказательство
Поскольку последовательность являются бесконечно большой, то имеется некоторая функция , так что для любого положительного числа M выполняется неравенство:
при .
Пусть при выполняется неравенство . Тогда при и имеем:
.
Итак, мы нашли функцию , так что для любого положительного числа M выполняется неравенство:
при .
Это означает, что последовательность являются бесконечно большой.
Свойство доказано.
Автор: Олег Одинцов. Опубликовано: Изменено:
