Свойства пределов последовательностей, связанных неравенствами
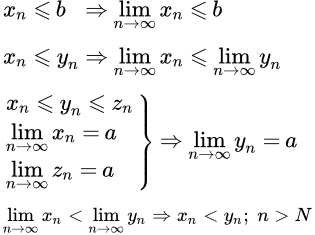
Формулировки свойств и теорем
Теорема о пределе последовательности, ограниченной с одной стороны
Пусть последовательность {xn} имеет конечный предел a : limn → ∞ xn = a . И пусть элементы этой последовательности, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b) . Тогда и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b) .
Доказательство ⇓
Следствие о пределе последовательности, ограниченной с двух сторон
Пусть последовательность {xn} имеет конечный предел a : limn → ∞ xn = a . И пусть элементы этой последовательности, начиная с некоторого номера, принадлежат замкнутому интервалу (сегменту) b ≤ xn ≤ c . Тогда и предел a также принадлежит этому интервалу: b ≤ a ≤ c .
Это свойство является следствием теоремы 1.
Следствие о пределах последовательностей, связанных неравенствами
Пусть последовательности {xn} и {yn} имеют конечные пределы a и b : limn → ∞ xn = a и limn → ∞ yn = b . И пусть элементы этих последовательностей, начиная с некоторого номера, удовлетворяют неравенству xn ≤ yn . Тогда a ≤ b .
Доказательство ⇓
Аналогичное свойство имеется и для бесконечно больших последовательностей.
Свойство неравенств бесконечно больших последовательностей
Если limn → ∞ βn = ∞ и, начиная с некоторого номера,
| γn | ≥ | βn | , то
limn → ∞ γn = ∞ .
Доказательство
В частности, если, начиная с некоторого номера,
γn ≥ βn , то
если limn → ∞ βn = + ∞ , то limn → ∞ γn = + ∞ ;
если limn → ∞ γn = – ∞ , то limn → ∞ βn = – ∞ .
Теорема о промежуточной последовательности
Пусть последовательности {xn} и {zn} сходятся к одному конечному числу a : limn → ∞ xn = limn → ∞ zn = a . И пусть элементы последовательности {yn} , начиная с некоторого номера, удовлетворяют неравенствам xn ≤ yn ≤ zn , то есть находятся в промежутке между элементами последовательностей {xn} и {zn} . Тогда эта последовательность также сходится к числу a : limn → ∞ yn = a .
Доказательство, Примеры.
Теорема о последовательностях, пределы которых связаны неравенством
Пусть последовательности {xn} и {yn} имеют конечные пределы a и b : limn → ∞ xn = a и limn → ∞ yn = b . Если a < b , то найдется такое натуральное число N , что для всех n > N выполняется неравенство xn < yn .
Доказательство ⇓
Доказательство свойств
Теорема о пределе последовательности, ограниченной с одной стороны
Все свойства ⇑ Пусть последовательность {xn} имеет конечный предел a : limn → ∞ xn = a . И пусть элементы этой последовательности, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b) . Тогда и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b) .
Доказательство
1) Рассмотрим случай xn ≥ b .
Поскольку существует предел limn → ∞ xn = a , то имеется функция Nx (ε ) такая, что, для любого положительного числа ε > 0 , выполняется система неравенств:
(1) | xn – a | < ε; n > Nx (ε ) .
По условию теоремы, начиная с некоторого номера, xn ≥ b . Предположим противное, что a < b . Тогда b – a > 0 – положительное число. Подставим в (1) ε = b – a :
| xn – a | < b – a; n > Nx (b – a ) .
Раскроем знак модуля и преобразуем:
– (b – a ) < xn – a < b – a ;
2a – b < xn < b; n > Nx (b – a ) .
То есть мы получили, что для всех номеров n , больших чем Nx (b – a ) , должно выполняться неравенство xn < b . Но это противоречит исходному утверждению, что начиная с некоторого номера, xn ≥ b .
2) Рассмотрим случай xn ≤ b .
Можно построить доказательство, как и для первого случая, но мы воспользуемся полученным выше результатом. Умножим неравенство xn ≤ b на –1 :
– xn ≥ – b .
Рассмотрим последовательность yn = – xn . Ее элементы, начиная с некоторого номера, удовлетворяют неравенству yn ≥ – b .
На основании арифметических свойств, последовательность {yn } имеет предел
A = limn → ∞ yn = – limn → ∞ xn = – a .
Тогда, на основании первой части этой теоремы, A ≥ – b . Или
– a ≥ – b ;
a ≤ b .
Теорема доказана.
Примечание
Если элементы последовательности, начиная с некоторого номера, удовлетворяют строгому неравенству xn > b (xn < b ) , то предел a последовательности {xn } все равно удовлетворяет нестрогому неравенству a ≥ b (a ≤ b ) .
Например, члены последовательности xn = 1n больше нуля: 1n > 0 .
Но limn → ∞ xn = 0 .
Следствие о пределах последовательностей, связанных неравенствами
Все свойства ⇑ Пусть последовательности {xn} и {yn} имеют конечные пределы a и b : limn → ∞ xn = a и limn → ∞ yn = b . И пусть элементы этих последовательностей, начиная с некоторого номера, удовлетворяют неравенству xn ≤ yn . Тогда a ≤ b .
Доказательство
Это свойство также является следствием теоремы о пределе последовательности, ограниченной с одной стороны ⇑.
Для доказательства рассмотрим последовательность {zn } с общим членом zn = yn – xn . Тогда, начиная с некоторого номера, zn ≥ 0 . На основании теоремы 1:
limn → ∞ zn ≥ 0 .
На основании арифметических свойств пределов:
limn → ∞ zn = limn → ∞ (yn – xn ) = b – a .
Тогда
b – a ≥ 0 ;
a ≤ b .
Теорема о последовательностях, пределы которых связаны неравенством
Все свойства ⇑ Пусть последовательности {xn} и {yn} имеют конечные пределы a и b : limn → ∞ xn = a и limn → ∞ yn = b . Если a < b , то найдется такое натуральное число N , что для всех n > N выполняется неравенство xn < yn .
Доказательство
Рассмотрим последовательность {zn } с элементами
zn = yn – xn .
Согласно арифметическим свойствам, эта последовательность сходится, и ее предел равен
limn → ∞ zn = limn → ∞ yn – limn → ∞ xn = b – a .
Это означает, что имеется функция Nz (ε ) такая, что для любого положительного числа ε > 0 выполняется система неравенств:
(5.1) | zn – (b – a ) | < ε; n > Nz (ε ) .
По условию b – a > 0 . Подставим в (5.1) ε = (b – a ) / 2 и введем обозначение N = Nz ((b – a ) / 2 ) . Тогда при n > N имеем:
| zn – (b – a ) | < (b – a ) / 2 ;
– (b – a ) / 2 < zn – (b – a ) < (b – a ) / 2 ;
(b – a ) / 2 < zn < 3(b – a ) / 2 .
Поскольку b – a > 0 , то
zn > 0 .
Или
yn – xn > 0 .
То есть при n > N ,
xn < yn .
Теорема доказана.
Автор: Олег Одинцов. Опубликовано: Изменено: