Определение бесконечно большой последовательности
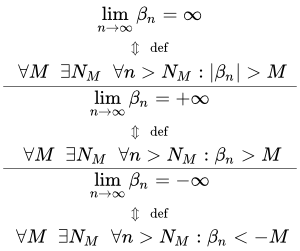
Определение
- Бесконечно большая последовательность
- Последовательность {βn} называется бесконечно большой последовательностью, если для любого, сколь угодно большого числа M, существует такое натуральное число NM, зависящее от M, что для всех натуральных n > NM выполняется неравенство
|βn| > M.
В этом случае пишут
.
Или при .
Говорят, что стремится к бесконечности, или сходится к бесконечности.
- Сходимость к плюс минус бесконечности
- Если , начиная с некоторого номера N0, то
( сходится к плюс бесконечности).
Если же , то
( сходится к минус бесконечности).
Запишем эти определения с помощью логических символов существования и всеобщности:
(1) .
(2) .
(3) .
Последовательности с пределами (2) и (3) являются частными случаями бесконечно большой последовательности (1). Из этих определений следует, что если предел последовательности равен плюс или минус бесконечности, то он также равен и бесконечности:
.
Обратное, естественно, не верно. Члены последовательности могут иметь чередующиеся знаки. При этом предел может равняться бесконечности, но без определенного знака.
Заметим также, что если какое-то свойство выполняется для произвольной последовательности с пределом равным бесконечности, то это же свойство выполняется и для последовательности, чей предел равен плюс или минус бесконечности.
Во многих учебниках по математическому анализу, в определении бесконечно большой последовательности указывается, что число M является положительным: M > 0. Однако это требование является лишним. Если его отменить, то никаких противоречий не возникает. Просто малые или отрицательные значения для нас не представляют никакого интереса. Нас интересует поведение последовательности при сколь угодно больших положительных значениях M. Поэтому, если возникнет необходимость, то M можно ограничить снизу любым, наперед заданным числом a, то есть считать, что M > a.
Когда же мы определяли ε - окрестность конечной точки, то требование ε > 0 является важным. При отрицательных значениях, неравенство вообще не может выполняться.
Окрестности бесконечно удаленных точек
Когда мы рассматривали конечные пределы, то ввели понятие окрестности точки. Напомним, что окрестностью конечной точки является открытый интервал, содержащий эту точку. Также мы можем ввести понятия окрестностей бесконечно удаленных точек.
- Окрестность точки ′бесконечность′
- Пусть M – произвольное число.
Окрестностью точки ′бесконечность′, , называется множество , где M > 0. - Окрестностью точки ′плюс бесконечность′
- , , называется множество .
- Окрестностью точки ′минус бесконечность′
- , , называется множество .
Строго говоря, окрестностью точки ′бесконечность′ является множество
(4) ,
где M1 и M2 – произвольные положительные числа. Мы будем использовать первое определение, , поскольку оно проще. Хотя, все сказанное ниже, также справедливо и при использовании определения (4).
Теперь мы можем дать единое определение предела последовательности, которое относится как к конечным, так и к бесконечным пределам.
- Универсальное определение предела последовательности
- Точка a (конечная или бесконечно удаленная) является пределом последовательности , если для любой окрестности этой точки существует такое натуральное число N, что все элементы последовательности с номерами принадлежат этой окрестности.
Таким образом, если предел существует, то за пределами окрестности точки a может находиться только конечное число членов последовательности, или пустое множество. Это условие является необходимым и достаточным. Доказательство этого свойства, точно такое, как для конечных пределов.
Свойство окрестности сходящейся последовательности
Для того, чтобы точка a (конечная или бесконечно удаленная) являлась пределом последовательности , необходимо и достаточно, чтобы за пределами любой окрестности этой точки находилось конечное число членов последовательности или пустое множество.
Доказательство.
Также иногда вводят понятия ε – окрестностей бесконечно удаленных точек.
Напомним, что ε – окрестностью конечной точки a называется множество .
Введем следующее обозначение. Пусть обозначает ε – окрестность точки a. Тогда для конечной точки,
.
Для бесконечно удаленных точек:
;
;
.
Используя понятия ε – окрестностей, можно дать еще одно универсальное определение предела последовательности:
- Определение предела последовательности через ε-окрестность
- Точка a (конечная или бесконечно удаленная) является пределом последовательности , если для любого положительного числа ε > 0 существует такое натуральное число Nε, зависящее от ε, что для всех номеров n > Nε члены xn принадлежат ε – окрестности точки a:
.
С помощью логических символов существования и всеобщности, это определение запишется так:
.
Примеры бесконечно больших последовательностей
Все примеры Сначала мы рассмотрим три простых похожих примера, а затем решим более сложный.
Пользуясь определением бесконечно большой последовательности показать, что
⇓, ⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.
Решение
Общий член заданной последовательности имеет вид:
.
Выпишем определение бесконечно большой последовательности:
(1) .
В нашем случае
.
Вводим числа и , связав их неравенствами:
.
По свойствам неравенств, если и , то
.
Заметим, что при это неравенство выполняется для любых n. Поэтому можно выбрать и так:
при ;
при .
Итак, для любого можно найти натуральное число , удовлетворяющее неравенству . Тогда для всех ,
.
Это означает, что . То есть последовательность является бесконечно большой.
Ответ
.
Пример 2
Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.
Решение
Выпишем определение предела последовательности, равному плюс бесконечности:
(2) .
Общий член заданной последовательности имеет вид:
.
Вводим числа и :
.
Отсюда видно, что если и , то
.
Тогда для любого можно найти натуральное число, удовлетворяющее неравенству , так что для всех ,
.
Это означает, что .
Ответ
При заданном , в качестве N можно взять любое натуральное число, удовлетворяющее следующему неравенству:
.
Пример 3
Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.
Решение
Выпишем определение предела последовательности, равному минус бесконечности:
(3) .
Общий член заданной последовательности имеет вид:
.
Вводим числа и :
.
Отсюда видно, что если и , то
.
Поскольку для любого можно найти натуральное число, удовлетворяющее неравенству , то
.
Ответ
При заданном , в качестве N можно взять любое натуральное число, удовлетворяющее следующему неравенству:
.
Пример 4
Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.
Решение
Выпишем общий член последовательности:
.
Выпишем определение предела последовательности, равному плюс бесконечности:
(2) .
Поскольку n есть натуральное число, n = 1, 2, 3, ..., то
;
;
.
Вводим числа и M, связав их неравенствами:
.
Отсюда видно, что если и , то
.
Итак, для любого числа M можно найти натуральное число, удовлетворяющее неравенству . Тогда для всех ,
.
Это означает, что .
Ответ
.
Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено:
