Примеры решений задач с помощью первого замечательного предела
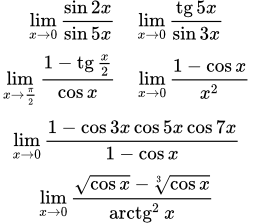
Применяемые формулы, свойства и теоремы
Здесь мы рассмотрим примеры решений задач на вычисление пределов, в которых используется первый замечательный предел и его следствия.
Ниже перечислены формулы, свойства и теоремы, которые наиболее часто применяются в подобного рода вычислениях.
- Первый замечательный предел и его следствия:
. - Тригонометрические формулы для синуса, косинуса, тангенса и котангенса:
;
;
;
при , ;
;
;
;
;
;
. - Арифметические свойства предела функции.
- Теоремы о пределе и непрерывности сложной функции.
Примеры решений
Все примеры Далее мы приводим подробные решения с объяснениями следующих пределов:
⇓, ⇓, ⇓, ⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Найти предел функции:
.
Решение с помощью первого замечательного предела
При , ; . Это неопределенность вида 0/0.
Для ее раскрытия, преобразуем функцию за знаком предела и разделим числитель и знаменатель дроби на x:
.
Заметим, что функцию в числителе можно представить как сложную:
,
где . Тогда для вычисления предела , делаем замену переменной . При . При . Таким образом,
.
Аналогичным образом, находим предел функции в знаменателе.
.
Делаем подстановку . При . При .
.
И наконец, применяем арифметические свойства предела функции:
.
Решение с помощью эквивалентных функций
Применим теорему о замене функций эквивалентными в пределе частного.
При . Из таблицы эквивалентных функций находим:
при ; при .
Тогда .
Ответ
.
Пример 2
Все примеры ⇑ Найдите предел:
.
Решение с помощью первого замечательного предела
При , , . Это неопределенность вида 0/0.
Преобразуем функцию за знаком предела:
.
Сделаем замену переменной . Поскольку и при , то
.
Аналогичным образом имеем:
.
Поскольку функция косинус непрерывна на всей числовой оси, то
.
Применяем арифметические свойства пределов:
.
Решение с помощью эквивалентных функций
Применим теорему о замене функций эквивалентными в пределе частного.
При . Из таблицы эквивалентных функций находим:
при ; при .
Тогда .
Ответ
.
Пример 3
Все примеры ⇑ Найти предел:
.
Решение
Подставим в числитель и знаменатель дроби:
;
.
Это неопределенность вида 0/0.
Попробуем решить этот пример с помощью первого замечательного предела. Поскольку в нем значение переменной стремится к нулю, то сделаем подстановку, чтобы новая переменная стремилась не к , а к нулю. Для этого от x перейдем к новой переменной t, сделав подстановку , . Тогда при , .
Предварительно преобразуем функцию за знаком предела, умножив числитель и знаменатель дроби на :
.
Подставим и воспользуемся приведенными выше тригонометрическими формулами.
;
;
.
Функция непрерывна при . Находим ее предел:
.
Преобразуем вторую дробь и применим первый замечательный предел:
.
В числителе дроби мы сделали подстановку .
Применяем свойство предела произведения функций:
.
Ответ
.Пример 4
Все примеры ⇑ Найти предел:
.
Решение
При , , . У нас неопределенность вида 0/0.
Преобразуем функцию под знаком предела. Применим формулу:
.
Подставим :
.
Преобразуем знаменатель:
.
Тогда
.
Поскольку и при , то сделаем подстановку , и применим теорему о пределе сложной функции и первый замечательный предел:
.
Применяем арифметические свойства предела функции:
.
Ответ
.
Пример 5
Все примеры ⇑ Найдите предел функции:
.
Решение
Нетрудно убедиться, что в этом примере мы имеем неопределенность вида 0/0. Для ее раскрытия, применим результат предыдущей задачи, согласно которому
.
Введем обозначение:
(П5.1) . Тогда
(П5.2) .
Из (П5.1) имеем:
.
Подставим в исходную функцию:
,
где ,
,
;
;
;
.
Используем (П5.2) и непрерывность функции косинус. Применяем арифметические свойства предела функции.
,
здесь m – отличное от нуля число, ;
;
;
.
Ответ
.
Пример 6
Все примеры ⇑ Найти предел:
.
Решение
При , числитель и знаменатель дроби стремятся к 0. Это неопределенность вида 0/0. Для ее раскрытия, преобразуем числитель дроби:
.
Применим формулу:
.
Подставим :
;
,
где .
Применим формулу:
.
Подставим :
;
,
где .
Числитель дроби:
.
Функция за знаком предела примет вид:
.
Найдем предел последнего множителя, учитывая его непрерывность при :
.
Применим тригонометрическую формулу:
.
Подставим ,
. Тогда
.
Разделим числитель и знаменатель на , применим первый замечательный предел и одно из его следствий:
.
Окончательно имеем:
.
Примечание 1. Также можно было применить формулу
, подставив .
Примечание 2. В конце мы могли применить теорему о замене функций эквивалентными в пределе частного.
Из таблицы эквивалентных функций находим:
при ; при .
Тогда .
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
