Решение пределов с корнями
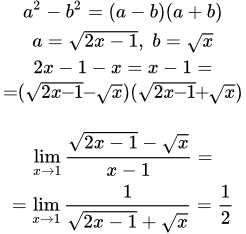
Методы решений
Для вычисления пределов с корнями, применяются приемы и методы, аналогичные методам вычисления пределов с многочленами (см. «Раскрытие неопределенностей с дробями», «Решение пределов с дробями из многочленов»). При этом возможны следующие дополнительные приемы, специфичные для функций с корнями.
1) Убрать корни с помощью подстановки, применяя теорему о пределе сложной функции. Примеры ⇓
2) Разделить числитель и знаменатель на xs (в случае неопределенности вида ∞/∞ при x → ∞), где s – некоторое подобранное число. Пример ⇓
3) Выразить бесконечно малые функции, содержащие корни, через бесконечно малые линейные функции, используя приведенные ниже формулы (то же самое в случае разности бесконечно больших функций). Примеры ⇓
4) Иногда удобно бесконечно малую функцию преобразовать в сумму или разность бесконечно малых функций, пределы от которых легко находятся. Пример ⇓
В последних двух случаях применяются следующие формулы:
;
;
;
. . . . . . . .
.
Например:
;
;
.
Эти же формулы применяют и для раскрытия разности бесконечно больших функций: .
Примеры решений
Все примеры Далее мы приводим подробные решения следующих примеров.
Найти предел последовательности:
решение ⇓
Найти следующие пределы функций с корнями:
⇓ , ⇓ , ⇓ , ⇓ , ⇓ .
Решение подстановкой
Пример 1
Все примеры ⇑ Найти предел:
.
Решение
Подставим . Тогда .
При .
Мы имеем неопределенность вида .
Замечаем, что от корня можно освободится, если сделать подстановку .
Тогда функцию за знаком предела можно представить как сложную:
,
где , .
Тогда нам нужно найти предел сложной функции
, где .
Применим теорему о пределе сложной функции. Но поскольку функция строго монотонна, то мы применим ее разновидность – теорему о пределе функции от монотонной функции.
Для этого сначала вычисляем предел . Поскольку функция непрерывна на всей области определения, то этот предел равен значению функции в точке :
.
Теперь вычисляем второй предел:
.
Он не содержит корней. То есть мы свели задачу к пределу от разности дробей многочленов. Применяем методы, изложенные на странице «Решение пределов с дробями из многочленов».
Разложим знаменатель на множители и приводим дроби к общему знаменателю:
;
.
Делим числитель и знаменатель на . При имеем:
.
Находим предел:
.
По теореме о пределе функции от монотонной функции,
.
Ответ
.
Пример 2
Все примеры ⇑ Найти предел последовательности:
.
Решение
Преобразуем элемент заданной последовательности, воспользовавшись свойствами корней:
.
Согласно свойств показательной функции,
.
Поскольку при , то согласно определению предела функции по Гейне, .
Если мы найдем предел функции
,
то согласно определению предела функции по Гейне, искомый предел заданной последовательности будет равняться этому пределу: , поскольку при .
Находим предел отношения многочленов, выделяя и сокращая в числителе и знаменателе множитель :
.
Ответ
.
Неопределенность ∞ / ∞
Пример 3
Все примеры ⇑ Найти предел отношения корней:
.
Решение
Здесь, при числитель и знаменатель стремятся к . У нас неопределенность вида . Для ее раскрытия, последовательно выносим бесконечно большую часть в числителе и знаменателе за скобки. При имеем:
;
;
;
;
.
Делим числитель и знаменатель на :
.
При .
Применяя арифметические свойства пределов функции, находим:
.
Ответ
.
Линеаризация бесконечно малых (больших) функций
Пример 4
Все примеры ⇑ Найти предел дроби с корнями:
.
Решение
Подставим в числитель и знаменатель:
;
.
Числитель и знаменатель обращаются в нуль. Мы имеем неопределенность вида 0/0.
Для ее раскрытия, линеаризуем бесконечно малые функции, используя формулу:
(П4.1) .
Подставим :
;
.
Отсюда
,
где
.
Подставим в (П4.1) :
;
.
Отсюда
,
где
.
Делим числитель и знаменатель на и находим предел:
.
Здесь , .
Ответ
.
Пример 5
Все примеры ⇑ Найти предел функции:
,
где
.
Решение
Подставим в числитель и знаменатель:
;
.
Мы имеем неопределенность вида 0/0.
Чтобы упростить вычисления, здесь удобно представить бесконечно малые функции в числителе и знаменателе в виде сумм и разностей других бесконечно малых функций:
(П5.1) .
Применим формулу:
.
Подставим :
.
Отсюда
, где .
Заметим, что .
Применим формулу:
.
Подставим :
.
Отсюда
, где .
Заметим, что .
Применим формулу:
.
Подставим :
.
Отсюда
, где .
.
Наконец, применим формулу:
.
Подставим :
.
Отсюда
, где .
.
Подставляем полученные выражения в (П5.1):
.
Делим числитель и знаменатель на x. В результате мы освобождаемся от неопределенности и находим предел непрерывной функции:
.
Можно было записать и так:
.
После чего вычислить пределы:
.
Ответ
.Пример 6
Все примеры ⇑ Найти предел функции с корнями при x стремящемся к бесконечности:
.
Решение
Поскольку, при , и , то мы имеем неопределенность вида +∞ – (+∞).
Применим формулу:
(П6.1) .
Подставим :
.
Отсюда, при имеем:
(П6.2) .
В числителе опять неопределенность +∞ – (+∞). Применяем формулу (П6.1) еще раз. Подставим :
.
Отсюда
.
Подставим в (П6.2):
,
где .
Теперь у нас неопределенность вида ∞/∞. Для раскрытия этой неопределенности, преобразуем знаменатель. Выделим бесконечно большую часть и вынесем ее за скобки. При имеем:
;
;
;
;
;
.
Делим числитель и знаменатель в функции на . При имеем:
.
Находим предел.
При , ,
.
Ответ
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин. Сборник задач по высшей математики. Том 1. Москва, 1957.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Б.П. Демидович. Сборник задач и упражнений по математическому анализу. Москва, 1997.
Автор: Олег Одинцов. Опубликовано: Изменено:
