Тангенс (tg x) и котангенс (ctg x) – свойства, графики, формулы

Справочные данные по тангенсу (tg x) и котангенсу (ctg x). Геометрическое определение, свойства, графики, формулы. Таблица тангенсов и котангенсов, производные, интегралы, разложения в ряды. Выражения через комплексные переменные. Связь с гиперболическими функциями.

Содержание

См. также:

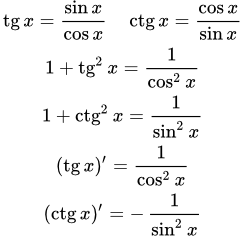
Геометрическое определение

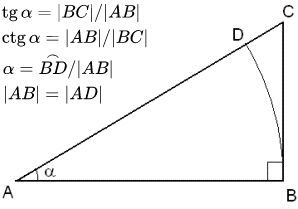
|BD| – длина дуги окружности с центром в точке A.
α – угол, выраженный в радианах.

Тангенс (tg α): – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине прилежащего катета |AB|.
Котангенс (ctg α): – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине противолежащего катета |BC|.

, где n - целое.
, где n - целое.

Принятые обозначения

Тангенс

В западной литературе тангенс обозначается так:
.
Также приняты следующие обозначения:
;
;
.

Котангенс

В западной литературе котангенс обозначается так:
.
Также приняты следующие обозначения:
;
;
.

Графики функций тангенс, y = tg x, и котангенс, y = ctg x

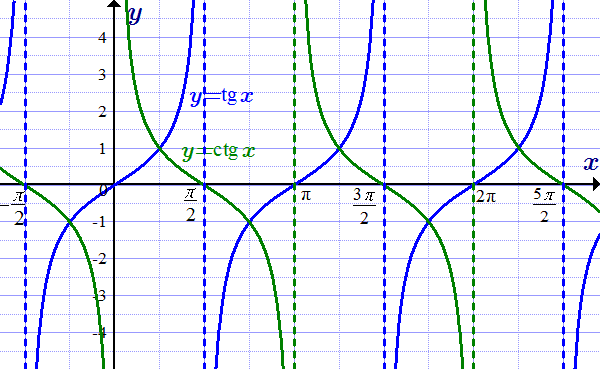
Свойства тангенса и котангенса

Периодичность

Функции y = tg x и y = ctg x периодичны с периодом π.

Четность

Функции тангенс и котангенс – нечетные.

Области определения и значений, возрастание, убывание

Функции тангенс и котангенс непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства тангенса и котангенса представлены в таблице (n - целое).

	y = tg x	y = ctg x
Область определения и непрерывность
Область значений	–∞ < y < +∞	–∞ < y < +∞
Возрастание		–
Убывание	–
Экстремумы	–	–
Нули, y = 0
Точки пересечения с осью ординат, x = 0	y = 0	–

Формулы

Выражения через синус и косинус

; ;
; ;
;

Формулы тангенса и котангенс от суммы и разности

Остальные формулы легко получить, например

Произведение тангенсов

Формула суммы и разности тангенсов

Таблица тангенсов и котангенсов

В данной таблице представлены значения тангенсов и котангенсов при некоторых значениях аргумента.

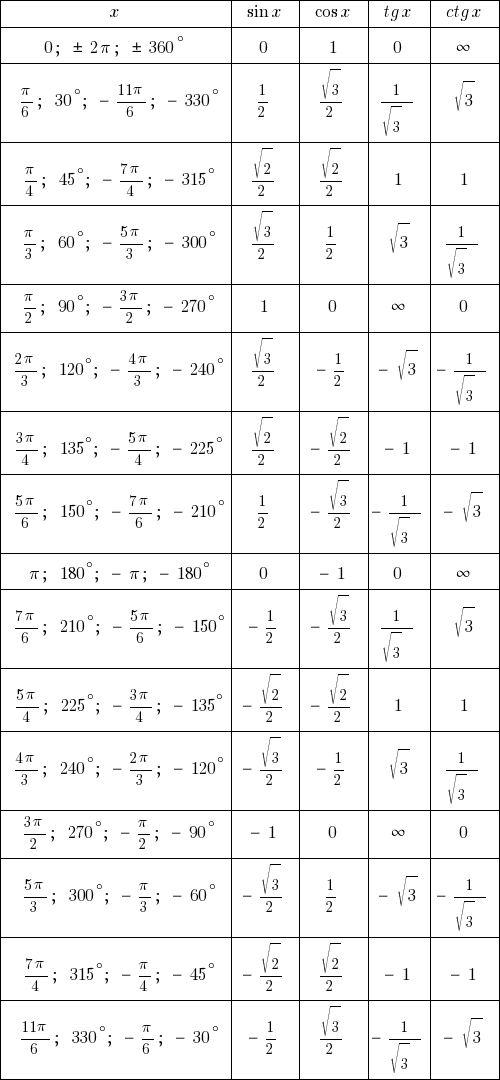
Выражения через комплексные числа

Выражения через гиперболические функции

;
;

Производные

; .

Производная n-го порядка по переменной x от функции :
.
Производная n-го порядка по переменной x от функции :
.
Вывод формул для тангенса > > >; для котангенса > > >

Интегралы

Разложения в ряды

Чтобы получить разложение тангенса по степеням x, нужно взять несколько членов разложения в степенной ряд для функций sin x и cos x и разделить эти многочлены друг на друга, . При этом получаются следующие формулы.

при .

при .
где B_n – числа Бернулли. Они определяются либо из рекуррентного соотношения:
;
;
где .
Либо по формуле Лапласа:
$B_n = (-1)^n \, n! \left| \begin{matrix} \frac1{2!} & 1 & 0 & ... & 0 \\ \frac1{3!} & \frac1{2!} & 1 & ... & 0 \\ \frac1{4!} & \frac1{3!} & \frac1{2!} & ... & 0 \\ ... & ... & ... & ... & ... \\ \frac1{(n+1)!} & \frac1{n!} & \frac1{(n-1)!} & ... & \frac12 \\ \end{matrix} \right|$

Обратные функции

Обратными функциями к тангенсу и котангенсу являются арктангенс и арккотангенс, соответственно.

Арктангенс, arctg

, где n - целое.

Арккотангенс, arcctg

, где n - целое.

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Г. Корн, Справочник по математике для научных работников и инженеров, 2012.

Автор: Олег Одинцов. Опубликовано: 19-02-2014 Изменено: 23-12-2018

См. также: