Доказательство первого замечательного предела и его следствий
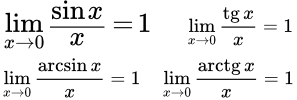
Первый замечательный предел и его следствия
Первый замечательный предел – это предел, на основе которого вычисляются производные тригонометрических функций.
Лемма. Первый замечательный предел
.
Доказательство ⇓
Следствия первого замечательного предела
;
;
.
Доказательство ⇓
Доказательство первого замечательного предела
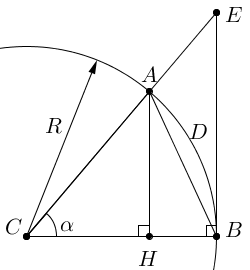
SCAB < SCADB < SCEB.
Пусть точки A и B лежат на окружности радиуса R с центром в точке C: |CA| = |CB| = R (см. рисунок). Через точку A проведем высоту AH треугольника ABC. Через точку B проведем перпендикуляр BE к отрезку BC до пересечения с прямой CA в точке E. Пусть α – угол, выраженный в радианах, между сторонами CA и CB:
.
Здесь – длина дуги окружности.
А) Рассмотрим случай .
Поскольку длина отрезка AB является кратчайшим расстоянием между точками A и B, то
.
Из прямоугольника ABH имеем:
;
.
Подставим :
.
Разделим на положительное число :
(1) .
Согласно приведенной ниже лемме ⇓,
.
Подставим сюда :
.
Умножим на положительное число :
(2) .
Б) Теперь рассмотрим отрицательные значения .
Тогда – положительное. Подставим в (3) и воспользуемся четностью косинуса и нечетностью синуса:
;
;
;
.
Таким образом, неравенства (3) выполняются как для положительных, так и для отрицательных значений :
(4) при .
В силу непрерывности функции косинус:
.
Переходим в (4) к пределу . Применяя теорему о промежуточной функции, получаем:
.
Наконец, обозначим переменную α буквой x:
.
Первый замечательный предел доказан.
Доказательство следствий первого замечательного предела
1) Докажем, что :
.
Здесь мы, кроме доказанного выше первого замечательного предела, использовали арифметические свойства пределов функций и непрерывность функции косинус.
Следствие 1) доказано.
2) Докажем, что :
.
Приведем пояснения к вычислениям, двигаясь с конца. Мы использовали первый замечательный предел: , применили арифметические свойства пределов функций: .
Далее мы воспользовались теоремой о пределе сложной функции. Поясним этот переход более подробно. Пусть
.
Тогда эту функцию можно представить как сложную:
,
где , .
Чтобы применить теорему о пределе сложной функции, нам нужно показать три вещи:
a) что существует предел ;
b) что существует такая проколотая окрестность точки , на которой
при .
c) что существует предел .
Покажем это.
a) Поскольку функция арксинус непрерывна на своей области определения, то предел равен значению функции в :
.
b) Если бы функция была непрерывной в точке , то и не было бы условия b), а предел равнялся бы значению функции в : . Но в нашем случае, функция не определена при , и поэтому не является непрерывной в . Нам нужно доказать, что существует такая проколотая окрестность точки , на которой
при .
Такая окрестность существует, поскольку функция строго монотонна и поэтому имеет значение только в одной точке. Это точка . Поскольку при , то на любой проколотой окрестности точки , . Пункт b) выполнен.
c) Выше мы показали, что существует предел
.
И, наконец, исходя из определения функции арксинус,
при .
Следствие 2) доказано.
3) Здесь доказательство аналогично предыдущему.
Поскольку , и при , то
.
Следствия доказаны.
Доказательство леммы
Определение длины дуги окружности
В классической математике мы научились определять расстояния между точками и вычислять длину отрезка. Положение точки A на плоскости определяется ее двумя координатами относительно заранее выбранной прямоугольной системы координат xy. Тогда длина отрезка AB есть расстояние между точками A и B:
.
Основываясь на этом, мы можем определить длину окружности средствами математического анализа.
Рассмотрим дугу окружности (см. рисунок ⇓). Разместим на ней произвольным образом n точек , нумеруя их от точки A к точке B. Число n тоже произвольно. Соединим точки попарно отрезками . В результате получим ломаную . Будем называть ее ломаной, вписанной в дугу окружности. Суммируя длины всех отрезков, мы получим длину ломаной :
.
Рассматривая произвольные ломаные, построенные таким способом, мы получим множество длин ломаных , вписанных в дугу .
- Длина дуги окружности
- Длиной дуги окружности называется верхняя грань множества длин всех ломаных, вписанных в эту дугу:
.
Доказательство леммы
Лемма
Пусть – дуга окружности с центром в точке C. И пусть и точка A принадлежит отрезку CE. Тогда
.
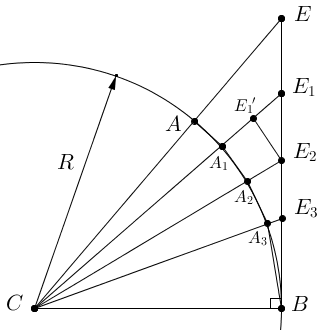
Доказательство
Рассмотрим произвольную ломаную , вписанную в дугу . Через центр окружности C и каждую вершину ломаной проведем отрезок до пересечения с отрезком BE в точке .
Через точку проведем отрезок , параллельно , до пересечения с отрезком в точке . Треугольники и равнобедренные и подобные. Из их подобия имеем:
.
Поскольку треугольник равнобедренный, то угол . Тогда . Используя теорему косинусов, имеем: .
Таким образом
, или
.
Выполняя подобные построения для остальных вершин ломаной, получим:
;
, где .
Поскольку в треугольнике , угол , то
.
Применяя эти неравенства, покажем, что длина ломаной меньше длины отрезка :
;
.
Переходя к точной верхней границе, получаем:
(Л1) .
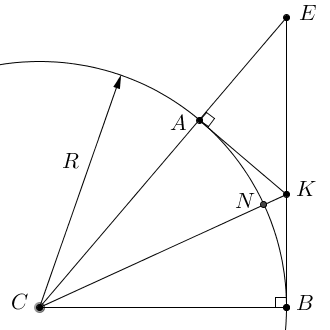
Теперь докажем, что .
Для этого из точки A проведем отрезок AK, перпендикулярно CE, чтобы точка K принадлежала EB. И пусть N – точка пересечения отрезка CK с дугой . Применяя (Л1) к треугольникам CAK и CKB, получим:
;
.
Из прямоугольника KAE имеем:
.
Тогда
.
Или .
Лемма доказана.
Автор: Олег Одинцов. Опубликовано: Изменено:
