Замена переменной при решении пределов
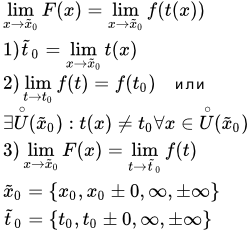
Краткое описание метода
Здесь мы рассмотрим вопрос о замене переменной при вычислении предела функции.
Пусть нам нужно вычислить предел:
(1) ,
где – конечное число , либо один из символов: . И пусть функцию можно представить в виде сложной:
.
Тогда мы применяем теоремы о пределе и непрерывности сложной функции. Для этого делаем замену переменной и разбиваем процесс вычисления исходного предела (1) на несколько частей.
1) Вычисляем предел .
2) Если – конечное число , и не является непрерывной в , то убеждаемся, что существует такая проколотая окрестность точки , на которой при .
3) Делаем замену переменной и вычисляем предел .
Здесь есть конечное число , либо один из символов: . Пояснения для значений предела и приводятся ниже ⇓.
Правила выполнения замены переменной
Если предела не существует, то замену переменной применять нельзя. Исходный предел может существовать, но нужно применять другие методы исследования.
Если является одним из символов , то второй пункт выполнен. Вычислив предел , сразу переходим к третьему пункту и вычисляем искомое значение (если существует).
Если является конечным числом и непрерывна в , то на основании определения непрерывной функции, мы переносим знак предела к аргументу функции:
.
Если же функция не является непрерывной в , то мы должны убедиться, что существует такая проколотая окрестность точки , на которой
(2) при .
В противном случае, в любой проколотой окрестности существуют точки , в которых принимает значение . Но при функция или не определена, или имеет значение, отличное от предельного (в противном случае была бы непрерывной в ). Поэтому предела не существует, несмотря на то, что существуют пределы и (см. пример ⇓).
Условие (2) выполняется, если существует такая проколотая окрестность точки , на которой строго монотонна. Монотонность может иметь разный характер слева и справа от . Например, слева функция возрастает; справа – убывает. То есть фактически, условие (2) выполняется, если задана явным аналитическим способом посредством элементарных функций, за исключением тригонометрических. А если в состав входят тригонометрические функции, или применяются другие способы задания функций, то необходимо провести исследование. В этом случае, при , возможно бесконечное число значений в любой окрестности .
Собственно в этом и заключается главное предостережение, которое необходимо учитывать, применяя подстановки при вычислении пределов.
Значения предела t0±0
Поясним, почему мы обозначили величину предела буквой с тильдой: . Такое обозначение означает, что предел при может быть либо конечным числом , либо одним из символов: . Символы общеприняты при записи величины предела (см. Бесконечный предел функции). Символ означает, что стремится к числу со стороны значений, меньших . То есть существует такая проколотая окрестность точки , на которой при . Аналогично, символ означает, что стремится к числу со стороны значений, больших . Для окончательного результата, и являются просто одним числом . Но для промежуточного результата, как в случае со сложной функцией, нам нужно различать, какие значения принимает аргумент функции – большие или меньшие .
Например, функция , при стремится к нулю: .
При , она стремится к плюс бесконечности:
.
Если положить , то .
Тогда для сложной функции :
.
Если положить , то ;
.
Пример
Все примеры Найти, если существует, предел функции:
.
Решение
Введем обозначение:
.
Функция определена для всех x, за исключением точки . Применим подстановку:
.
Представим как сложную функцию:
, где .
1) Находим предел
.
Поскольку при и функция синус ограничена: , то согласно теореме о произведении ограниченной функции на бесконечно малую,
.
Таким образом, при , первый предел является конечным числом:
.
2) Функция не является непрерывной в точке , поскольку она в ней не определена, так как знаменатель дроби равен нулю. Поэтому мы должны доказать, что существует такая проколотая окрестность точки , на которой при .
Однако, такой окрестности не существует.
Рассмотрим уравнение:
.
Согласно свойствам функции синус, это уравнение выполняется, если
, где n – целое.
Отсюда
.
Если в качестве n мы возьмем натуральные числа , то получим последовательность, с элементами . Поскольку , то эта последовательность сходится к единице при . Таким образом, в любой окрестности точки , существует бесконечное число элементов последовательности , для которых . Второе условие не выполнено.
Несмотря на то, что существуют пределы и , предела исходной функции не существует, поскольку существует сходящаяся к 1 последовательность, на которой не определена.
Ответ
Предела не существует.
Автор: Олег Одинцов. Опубликовано: Изменено:
