Предел и непрерывность сложной функции
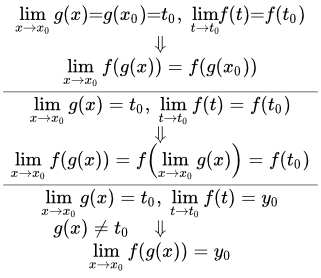
Формулировки теорем
Теорема о непрерывности сложной функции
Пусть функция t = g(x) непрерывна в точке x0. И пусть функция f(t) непрерывна в точке t0 = g(x0).
Тогда сложная функция f(g(x)) непрерывна в точке x0.
Доказательство ⇓
Теорема о пределе непрерывной функции от функции
Пусть существует предел функции t = g(x) при x → x0, и он равен t0:
.
Здесь точка x0 может быть конечной или бесконечно удаленной: .
И пусть функция f(t) непрерывна в точке t0.
Тогда существует предел сложной функции f(g(x)), и он равен f(t0):
.
Доказательство ⇓
Эта теорема означает, что знак предела можно применять к аргументу непрерывной функции:
.
По сравнению с предыдущей теоремой, здесь на функцию g(x) наложено менее жесткое условие. А именно: функция g(x) может быть не определена в точке x0, или ее значение в этой точке может отличаться от t0. Также точка x0 может быть бесконечно удаленной.
Наконец, если и не является непрерывной в точке , и не является непрерывной в точке , то применяют теорему о пределе сложной функции.
Теорема о пределе сложной функции
Пусть функции и имеют пределы:
;
.
И пусть существует такая проколотая окрестность точки , на которой
.
Тогда существует предел сложной функции , и он равен :
.
Здесь – конечные или бесконечно удаленные точки: . Окрестности и соответствующие им пределы могут быть как двусторонние, так и односторонние.
Доказательство
Теорема о пределе сложной функции применяется в том случае, когда функция не определена в точке или имеет значение, отличное от предельного . Для применения этой теоремы, должна существовать проколотая окрестность точки , в которой множество значений функции не содержит точку :
.
Окрестность , в которой g(x) ≠ t0 существует, если существует такая проколотая окрестность точки , в которой функция g строго монотонна. Монотонность может иметь разный характер слева и справа от . Например, слева функция возрастает; справа – убывает.
На этот случай имеется теорема о пределе функции от монотонной функции.
Доказательство теорем
Теорема о непрерывности сложной функции
Все теоремы ⇑ Пусть функция t = g(x) непрерывна в точке x0. И пусть функция f(t) непрерывна в точке t0 = g(x0).
Тогда сложная функция f(g(x)) непрерывна в точке x0.
Доказательство
1. Покажем сначала, что существует такая окрестность точки , на которой определена сложная функция .
Воспользуемся определением непрерывности функции в точке по Коши. Поскольку функция непрерывна в точке , то она определена на некоторой окрестности этой точки, и имеется такая функция , так что для любого ,
(1.1) при .
Здесь конечно подразумевается, что функция выбрана так, что окрестность принадлежит области определения функции .
Поскольку функция непрерывна в точке , то она определена на некоторой окрестности этой точки, и имеется такая функция , так что для любого ,
(1.2) при .
Здесь также подразумевается, что окрестность лежит в области определения функции .
Таким образом, при некотором фиксированном положительном значении , функция определена, по крайней мере на окрестности точки , и ее множество значений лежит в окрестности , на которой определена функция . Поэтому существует такая окрестность точки :
,
на которой определена сложная функция .
2. Теперь покажем, что
.
Перепишем неравенства (1.1) и (1.2), справедливые для любых и :
(1.1) при .
(1.2) при .
Возьмем произвольное положительное число . Тогда на основании (1.1) имеем:
при .
Поскольку и , то из (1.2) следует, что
при .
Тогда
при .
Тем самым мы нашли такую функцию , при которой, для любого ,
при .
Это означает, что
.
Теорема доказана.
Теорема о пределе непрерывной функции от функции
Все теоремы ⇑ Пусть существует предел функции t = g(x) при x → x0, и он равен t0:
.
Здесь точка x0 может быть конечной или бесконечно удаленной: .
И пусть функция f(t) непрерывна в точке t0.
Тогда существует предел сложной функции f(g(x)), и он равен f(t0):
.
Доказательство
1. Покажем сначала, что существует такая проколотая окрестность точки , на которой определена сложная функция .
Воспользуемся определением непрерывности функции в точке по Коши. Поскольку функция непрерывна в точке , то она определена на некоторой окрестности этой точки, и имеется такая функция , так что для любого ,
(2.1) при .
Здесь конечно подразумевается, что окрестность лежит в окрестности , на которой определена функция .
Воспользуемся определением предела функции в точке по Коши. Поскольку функция имеет предел в точке , то она определена на некоторой проколотой окрестности этой точки, и для любого , существует положительное число , зависящее от , так что
(2.2) при .
Здесь означает проколотую δ - окрестность точки . Подразумевается, что эта окрестность лежит в окрестности , на которой определена функция .
Таким образом, при некотором фиксированном положительном значении , функция определена, по крайней мере на проколотой окрестности точки , и ее множество значений лежит в окрестности , на которой определена функция . Тем самым мы нашли такую окрестность точки :
,
на которой определена сложная функция .
2. Теперь покажем, что
.
Перепишем неравенства (2.1) и (2.2), справедливые для любых и :
(2.1) при .
(2.2) при .
Возьмем произвольное положительное число . Тогда на основании (2.1) имеем:
при .
Поскольку , то из (2.2) следует, что
при .
Тогда
при .
Тем самым мы нашли такую функцию , при которой, для любого ,
при .
Это означает, что
.
Теорема доказана.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Автор: Олег Одинцов. Опубликовано: Изменено:
