Определение функции
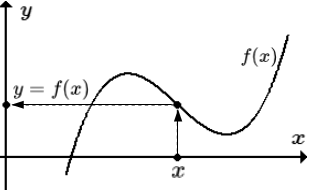
Определение функции
- Функцией
- y = f(x) называется закон (правило, отображение), согласно которому, каждому элементу x множества X ставится в соответствие один и только один элемент y множества Y.
- Область определения функции
- Множество X называется областью определения функции. Область определения иногда называют
множеством определения или множеством задания функции. - Множество значений функции
- Множество элементов y ∈ Y, которые имеют прообразы во множестве X, называется множеством значений функции, или областью значений.
- Аргумент функции
- Элемент x ∈ X называют аргументом функции или независимой переменной.
- Значение функции
- Элемент y ∈ Y называют значением функции или зависимой переменной.
- Характеристика функции
- Само отображение f называется характеристикой функции.
Характеристика f обладает тем свойством, что если два элемента и из множества определения имеют равные значения: , то .
Символ, обозначающий характеристику, может совпадать с символом элемента значения функции. То есть можно записать так: . При этом стоит помнить, что y – это элемент из множества значений функции, а – это правило, по которому для элемента x ставится в соответствие элемент y.
Сам процесс вычисления функции состоит из трех шагов. На первом шаге мы выбираем элемент x из множества X. Далее, с помощью правила , элементу x ставится в соответствие элемент множества Y. На третьем шаге этот элемент присваивается переменной y.
- Частным значением функции
- называют значение функции при выбранном (частном) значении ее аргумента.
- Графиком функции
- f называется множество пар .
Сложные функции
- Сложная функция
- Пусть заданы функции и . Причем область определения функции f содержит множество значений функции g. Тогда каждому элементу t из области определения функции g соответствует элемент x, а этому x соответствует y. Такое соответствие называют сложной функцией: . Сложную функцию также называют
композицией или суперпозицией функций и иногда обозначают так: .
В математическом анализе принято считать, что если характеристика функции обозначена одной буквой или символом, то она задает одно и то же соответствие. Однако, в других дисциплинах, встречается и другой способ обозначений, согласно которому отображения с одной характеристикой, но разными аргументами, считаются различными. То есть отображения и считаются различными. Приведем пример из физики. Допустим мы рассматриваем зависимость импульса от координаты . И пусть мы имеем зависимость координаты от времени . Тогда зависимость импульса от времени является сложной функцией . Но ее, для краткости, обозначают так: . При таком подходе и – это различные функции. При одинаковых значениях аргументов они могут давать различные значения. В математике такое обозначение не принято. Если требуется сокращение, то следует ввести новую характеристику. Например . Тогда явно видно, что и – это разные функции.
Действительные функции
Область определения функции и множество ее значений могут быть любыми множествами.
Например, числовые последовательности – это функции, областью определения которых является множество натуральных чисел, а множеством значений – вещественные или комплексные числа.
Векторное произведение тоже функция, поскольку для двух векторов и имеется только одно значение вектора . Здесь областью определения является множество всех возможных пар векторов . Множеством значений является множество всех векторов.
Логическое выражение является функцией. Ее область определения – это множество действительных чисел (или любое множество, в котором определена операция сравнения с элементом “0”). Множество значений состоит из двух элементов – “истина” и “ложь”.
В математическом анализе большую роль играют числовые функции.
- Числовая функция
- – это функция, значениями которой являются действительные или комплексные числа.
- Действительная или вещественная функция
- – это функция, значениями которой являются действительные числа.
Максимум и минимум
Действительные числа имеют операцию сравнения. Поэтому множество значений действительной функции может быть ограниченным и иметь наибольшее и наименьшее значения.
- Ограниченная сверху (снизу) функция
- Действительная функция называется ограниченной сверху (снизу), если существует такое число M, что для всех выполняется неравенство:
. - Ограниченная функция
- Числовая функция называется ограниченной, если существует такое число M, что для всех :
.
- Максимумом M (минимумом m) функции
- f, на некотором множестве X, называют значение функции при некотором значении ее аргумента , при котором для всех ,
.
Верхняя и нижняя грани
- Верхняя грань (точная верхняя граница) функции
- Верхней гранью или точной верхней границей действительной, ограниченной сверху функции называют наименьшее из чисел, ограничивающее область ее значений сверху. То есть это такое число s, для которого:
1) для всех ;
2) для любого , найдется такой аргумент , значение функции от которого превосходит s′: .
Верхняя грань функции может обозначаться так:
.
Верхней гранью неограниченной сверху функции является бесконечно удаленная точка . - Нижняя грань (точная нижняя граница) функции
- Нижней гранью или точной нижней границей действительной, ограниченной снизу функции называют наибольшее из чисел, ограничивающее область ее значений снизу. То есть это такое число i, для которого:
1) для всех ;
2) для любого , найдется такой аргумент , значение функции от которого меньше чем i′: .
Нижняя грань функции может обозначаться так:
.
Нижней гранью неограниченной снизу функции является бесконечно удаленная точка .
Таким образом, любая действительная функция, на не пустом множестве X, имеет верхнюю и нижнюю грани. Но не всякая функция имеет максимум и минимум.
В качестве примера рассмотрим функцию , заданную на открытом интервале .
Она ограничена, на этом интервале, сверху значением 1 и снизу – значением 0:
для всех .
Эта функция имеет верхнюю и нижнюю грани:
.
Но она не имеет максимума и минимума.
Если мы рассмотрим туже функцию на отрезке , то она на этом множестве ограничена сверху и снизу, имеет верхнюю и нижнюю грани и имеет максимум и минимум:
для всех ;
;
.
Монотонные функции
- Возрастающая (убывающая) функция
- Пусть функция определена на некотором множестве действительных чисел X. Функция называется строго возрастающей (строго убывающей), если для всех таких что выполняется неравенство:
.
Функция называется неубывающей (невозрастающей), если для всех таких что выполняется неравенство:
. - Монотонная функция
- Функция называется монотонной, если она неубывающая или невозрастающая.
Многозначные функции
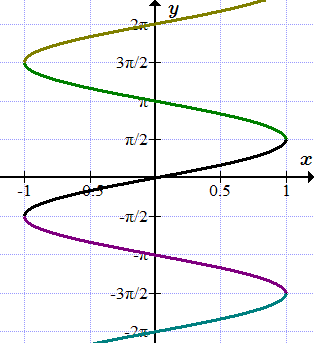
Как следует из определения функции, каждому элементу x из области определения, ставится в соответствие только один элемент из множества значений. Но существуют такие отображения, в которых элемент x имеет несколько или бесконечное число образов.
В качестве примера рассмотрим функцию арксинус: . Она является обратной к функции синус и определяется из уравнения:
(1) .
При заданном значении независимой переменной x, принадлежащему интервалу , этому уравнению удовлетворяет бесконечно много значений y (см. рисунок).
Наложим на решения уравнения (1) ограничение. Пусть
(2) .
При таком условии, заданному значению , соответствует только одно решение уравнения (1). То есть соответствие, определяемое уравнением (1) при условии (2) является функцией.
Вместо условия (2) можно наложить любое другое условие вида:
(2.n) ,
где n – целое. В результате, для каждого значения n, мы получим свою функцию, отличную от других. Множество подобных функций является многозначной функцией. А функция, определяемая из (1) при условии (2.n) является ветвью многозначной функции.
- Многозначная функция
- – это совокупность функций, определенных на некотором множестве.
- Ветвь многозначной функции
- – это одна из функций, входящих в многозначную функцию.
- Однозначная функция
- – это функция.
Сужение и продолжение функции
Выше мы указали, что если область определения функции синус, , сузить до отрезка , то полученная в результате новая функция будет строго монотонной на этом отрезке и иметь обратную функцию. Такая операция называется сужением функции. В результате ее применения получается новая функция, которая в данном примере обозначается так: .
- Сужение функции
- Пусть функция определена на множестве X. И пусть множество M является его подмножеством: . Определим функцию так, чтобы ее областью определения было множество M. И пусть на этом множестве она принимает те же значения, что и функция :
.
Тогда функция называется сужением функции f на множество M. Сужение функции обозначают так:
, или . - Продолжение функции
- Пусть функция определена на множестве X, а функция – на множестве M, которое является подмножеством X: . И пусть функция является сужением функции на множество M. Тогда функция называется продолжением функции g на множество X.
Выполнить операцию сужения функции на заданное множество можно только одним способом. А вот выполнить продолжение можно бесконечным числом способов. Особую роль продолжение играет в теории функций комплексного переменного. Там показывается, что если функция является аналитической (то есть имеет производную) на некотором множестве M, то существует только единственное ее аналитическое продолжение на множество X.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено:
