Критерий Коши существования предела функции
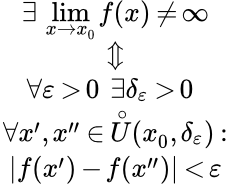
Определение
- Условие Коши
- Функция f(x), определенная на некоторой проколотой окрестности конечной или бесконечно удаленной точки x0 удовлетворяет условию Коши, если для любого ε > 0 существует такая проколотая окрестность точки x0, так что, для любых точек и из этой окрестности, выполняется неравенство:
|f(x′) – f(x′′)| < ε.
Более кратко условие Коши можно записать так:
.
Критерий Коши существования предела функции
Теорема
Для того, чтобы функция f(x), определенная на некоторой проколотой окрестности конечной или бесконечно удаленной точки x0, имела в этой точке конечный предел, необходимо и достаточно, чтобы выполнялось условие Коши:
.
Доказательство
Доказательство необходимости
Пусть функция имеет в точке конечный предел
.
Согласно определению предела функции по Коши это означает, что имеется такая функция , так что для любого числа выполняется неравенство
при .
Тогда при выбранном числе и при имеем:
.
Положим . Тогда
при .
То есть мы нашли такую функцию , так что для любого числа выполняется неравенство
при .
Это означает, что выполняется условие Коши.
Доказательство достаточности
Пусть в точке выполняется условие Коши. То есть существует такая функция , так что для любого числа выполняется неравенство
(1) при .
Докажем, что функция имеет в точке конечный предел
.
Для доказательства мы применим определение предела функции по Гейне и Критерий Коши сходимости последовательности.
Пусть есть произвольная последовательность, элементы которой принадлежат проколотой окрестности , на которой определена функция . И пусть эта последовательность сходится к :
.
Рассмотрим последовательность . Сначала мы докажем, что она сходится. Затем докажем, что любые такие последовательности сходятся к одному числу.
Доказательство сходимости последовательности
Подставим в (1) и :
(2) при .
Воспользуемся универсальным определением предела последовательности. Поскольку , то для любой окрестности точки существует такое натуральное число , что все элементы последовательности с номерами принадлежат этой окрестности. Применим это определение к окрестности . Тогда для любого числа существует такое число , так что
при .
Введем обозначение:
.
Тогда условие (2) примет вид:
при .
Но это есть условие Коши для последовательности . Поэтому она сходится.
Доказательство единственности предела
Допустим противное. Пусть существуют две последовательности и , элементы которых принадлежат области определения функции и сходящиеся к , но последовательности и сходятся к разным пределам:
.
Составим новую последовательность из последовательностей и , чередованием их членов:
.
Последовательность сходится к . Но последовательность не имеет предела, поскольку содержит две подпоследовательности и , сходящиеся к различным числам (см. свойства подпоследовательностей).
Возникает противоречие, поскольку, как мы только что доказали, любая последовательность должна иметь предел, если и .
Теорема доказана.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Автор: Олег Одинцов. Опубликовано:
