Определение предела функции на бесконечности
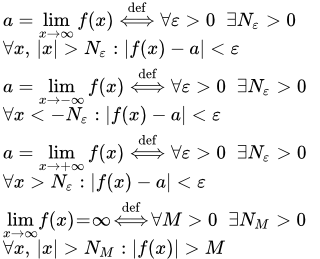
Конечный предел функции на бесконечности
|f(x) – a| < ε при |x| > N
- Предел функции по Коши на бесконечности
- Число a называется пределом функции f(x) при x стремящемся к бесконечности (), если
1) существует такая окрестность бесконечно удаленной точки |x| > K, на которой функция определена (здесь K – положительное число);
2) для любого, сколь угодно малого положительного числа ε > 0, существует такое число Nε > K, зависящее от ε, что для всех x, |x| > Nε, значения функции принадлежат ε - окрестности точки a:
|f(x) – a| < ε.
Предел функции на бесконечности обозначается так:
.
Или при .
Также часто используется следующее обозначение:
.
Запишем это определение, используя логические символы существования и всеобщности:
.
Здесь подразумевается, что значения принадлежат области определения функции.
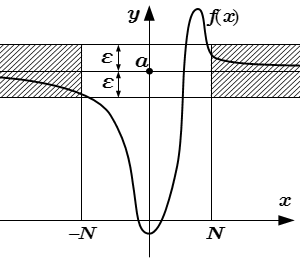
Односторонние пределы
|f(x) – a| < ε при x < –N
Часто встречаются случаи, когда функция определена только для положительных или отрицательных значений переменной x (точнее в окрестности точки или ). Также пределы на бесконечности для положительных и отрицательных значений x могут иметь различные значения. Тогда используют односторонние пределы.
Левый предел в бесконечно удаленной точке или предел при x стремящемся к минус бесконечности () определяется так:
.
Правый предел в бесконечно удаленной точке или предел при x стремящемся к плюс бесконечности ():
.
Односторонние пределы на бесконечности часто обозначают так:
; .
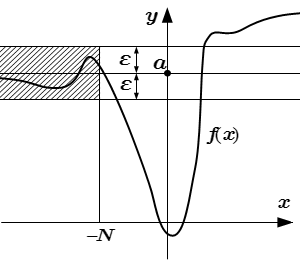
Бесконечный предел функции на бесконечности
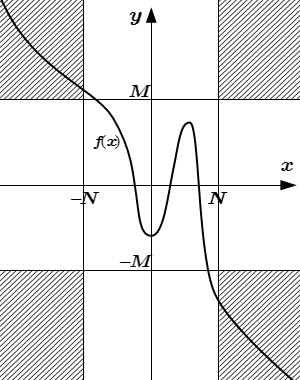
|f(x)| > M при |x| > N
- Бесконечный предел функции по Коши на бесконечности
- Предел функции f(x) при x стремящемся к бесконечности (), равен бесконечности, если
1) существует такая окрестность бесконечно удаленной точки |x| > K, на которой функция определена (здесь K – положительное число);
2) для любого, сколь угодно большого числа M > 0, существует такое число NM > K, зависящее от M, что для всех x, |x| > NM, значения функции принадлежат окрестности бесконечно удаленной точки:
|f(x)| > M.
Бесконечный предел при x стремящемся к бесконечности обозначают так:
.
Или при .
С помощью логических символов существования и всеобщности, определение бесконечного предела функции можно записать так:
.
Аналогично вводятся определения бесконечных пределов определенных знаков, равных и :
.
.
Определения односторонних пределов на бесконечности.
Левые пределы.
.
.
.
Правые пределы.
.
.
.
Определение предела функции по Гейне
- Предел функции по Гейне на бесконечности
- Число a (конечное или бесконечно удаленное) называется пределом функции f(x) в бесконечно удаленной точке x0:
,
если
1) существует такая окрестность бесконечно удаленной точки x0, на которой функция определена (здесь или или );
2) для любой последовательности {xn}, сходящейся к x0: ,
элементы которой принадлежат окрестности , последовательность {f(xn)} сходится к a:
.
Если в качестве окрестности взять окрестность бесконечно удаленной точки без знака: , то получим определение предела функции при x стремящемся к бесконечности, . Если взять левостороннюю или правостороннюю окрестность бесконечно удаленной точки x0: или , то получим определение предела при x стремящемся к минус бесконечности и плюс бесконечности, соответственно.
Определения предела по Гейне и Коши эквивалентны.
Примеры
Все примеры Далее мы приводим подробные решения двух примеров, в которых, используя определение Коши, нужно показать, что пределы имеют определенные значения:
⇓;
⇓, ⇓, где .
Пример 1
Все примеры ⇑ Используя определение Коши показать, что
.
Решение
Введем обозначения:
.
Найдем область определения функции . Поскольку числитель и знаменатель дроби являются многочленами, то функция определена для всех x кроме точек, в которых знаменатель обращается в нуль. Найдем эти точки. Решаем квадратное уравнение. ;
.
Корни уравнения:
; .
Поскольку , то и .
Поэтому функция определена при . Это мы будем использовать в дальнейшем.
Выпишем определение конечного предела функции на бесконечности по Коши:
.
Преобразуем разность:
.
Разделим числитель и знаменатель на и умножим на –1:
.
Пусть .
Тогда
;
;
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .
Поскольку всегда можно увеличить, то возьмем . Тогда для любого ,
при .
Это означает, что .
Пример 2
Все примеры ⇑ Пусть .
Используя определение предела по Коши показать, что:
1) ;
2) .
1) Решение при x стремящемся к минус бесконечности
Поскольку , то функция определена для всех x.
Выпишем определение предела функции при , равного минус бесконечности:
.
Пусть . Тогда
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что для любого положительного числа M, имеется число , так что при ,
.
Это означает, что .
2) Решение при x стремящемся к плюс бесконечности
Преобразуем исходную функцию. Умножим числитель и знаменатель дроби на и применим формулу разности квадратов:
.
Имеем:
.
Выпишем определение правого предела функции при :
.
Введем обозначение: .
Преобразуем разность:
.
Умножим числитель и знаменатель на :
.
Пусть
.
Тогда
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при и .
Поскольку это выполняется для любого положительного числа , то
.
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано:
