Выражение обратных тригонометрических функций комплексного переменного через логарифм
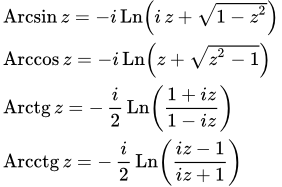
Формулы обратных тригонометрических функций
Обратные тригонометрические функции выражаются через натуральные логарифмы следующим образом:
Здесь стоит подчеркнуть, что все эти функции многозначны и обозначают всю совокупность значений в целом. Везде подразумевается, что квадратный корень имеет два знака: "+" и "–", а логарифм имеет бесконечное множество значений, отличающихся на 2πin, где n - целое. То есть, например, под арксинусом имеется в виду вся совокупность значений:
.
Такое правило распространяется на все многозначные функции комплексного переменного и их названия начинаются с большой буквы. Названия с маленькой буквы означают однозначную ветвь функции, заданной на определенной области Римановой поверхности.
Ниже приводится вывод этих формул.
Арксинус
Пусть f = arcsin z.
Чтобы выразить arcsin z через элементарные функции, решаем уравнение:
Выразим sin f через комплексные переменные:
Умножим на 2 i eif
Решаем квадратное уравнение
Логарифмируем
Умножаем на -i
Далее следует разобраться со знаком ±
. С точки зрения комплексных переменных, квадратный корень всегда имеет два значения, различающихся знаком плюс
и минус
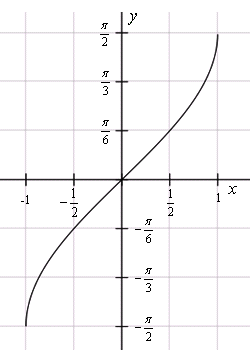
. Поэтому корень всегда подразумевает неоднозначность. Выберем такой знак, чтобы формула была справедлива для главного значения арксинуса. То есть для действительных значения арксинуса f = arcsin z должны находится в интервале
Рассмотрим знак +
. Положим z = 0.
То есть знак +
соответствует главному значению арксинуса, которое имеет множество значений при
Если мы возьмем знак –
, то
То есть знак –
соответствует ветви арксинуса, которая имеет множество значений при
Остальные ветви получаются вследствие многозначности логарифма. Выразим выражение под знаком логарифма через модуль r и аргумент φ:
где n - целое. Тогда
То есть многозначность логарифма дает ветви, которые отстоят друг от друга на величину 2π, что соответствует периоду синуса.
Итак,
Арккосинус
Выполняем аналогичные вычисления для арккосинуса. Пусть f = arccos z.
Рассмотрим уравнение:
Умножим на 2 eif
Логарифмируем
Если взять знак +
, то при z = 0 имеем:
Знак +
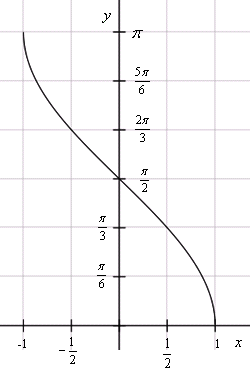
соответствует главному значению арккосинуса, которое имеет множество значений при
Если бы мы взяли знак –
, то
То есть знак –
соответствует ветви арккосинуса, которая имеет множество значений при .
Итак,
Арктангенс
Для арктангенса, пусть f = Arctg z.
Рассмотрим уравнение:
Умножим числитель и знаменатель на eif и выполняем преобразования
Логарифмируем:
;
.
Рассмотрим действительные z. Представим комплексную функцию под знаком логарифма в алгебраической форме:
,
где .
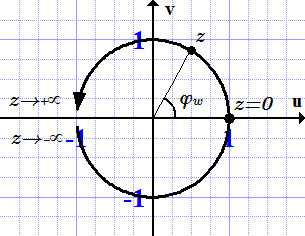
При . Это соответствует главному значению арктангенса, .
При . При этом аргумент функции возрастает от до : . Тогда
.
При . При этом аргумент функции убывает от до : . Тогда .
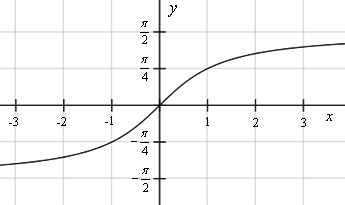
Все это соответствует главному значению арктангенса, у которого
;
.
Итак,
.
Мы можем образовать листы Римановой поверхности, подчинив их условию:
.
Тогда лист с , при действительных z, даст нам главное значение арктангенса. На остальных листах к функции w добавится множитель , что приведет к увеличению значения арктангенса на . Эти значения соответствуют другим ветвям арктангенса.
Арккотангенс
Пусть f = arcctg z.
Рассмотрим уравнение:
или
Это уравнение такое, как для тангенса, только нужно заменить z на :
;
.
Также рассмотрим действительные z. Представим комплексную функцию под знаком логарифма в алгебраической форме:
,
где .
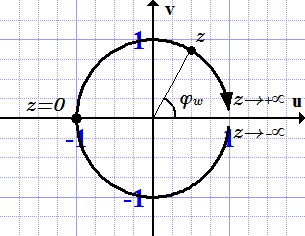
При . Это соответствует главному значению арккотангенса, .
При . При этом аргумент функции убывает от до : . Тогда .
При . При этом аргумент функции возрастает от до : . Тогда .
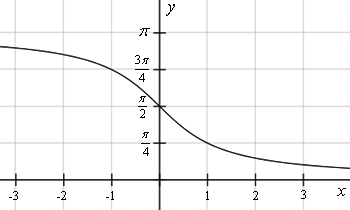
Все это соответствует главному значению арккотангенса, у которого
;
.
Итак,
.
Мы можем образовать листы Римановой поверхности, подчинив их условию:
.
Тогда лист с , при действительных z, даст нам главное значение арккотангенса. На остальных листах к функции w добавится множитель , что приведет к увеличению значения арккотангенса на . Эти значения соответствуют другим ветвям арктангенса.
Автор: Олег Одинцов. Опубликовано: Изменено:
