Тригонометрическая формула Виета для решения кубических уравнений
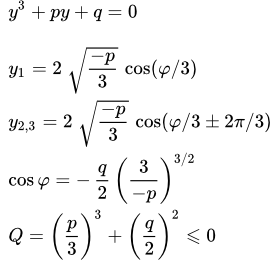
Формула Виета
Рассмотрим кубическое уравнение:
(1) .
Сделаем подстановку:
.
Получаем уравнение приведенного вида:
(2) ,
где
(3) ; .
Тригонометрическая формула Виета, для корней , , приведенного кубического уравнения (2), имеет вид:
(4) ;
(5) ;
где
(6) ; .
Условие применимости формулы Виета
Поскольку , то формула Виета применима при
.
Действительно, из (6) имеем:
; .
Возводим в квадрат и выполняем преобразования:
;
;
.
Как показано на странице “Решение кубических уравнений”, при выполнении условия , кубическое уравнение имеет три действительных корня. То есть формула Виета применяется в том случае, когда кубическое уравнение имеет действительные корни.
Вывод формулы Виета
Для вывода формулы Виета, используем формулу Кардано:
(7) ;
(8) ;
(9) ;
(10) ;
(11) .
Считаем, что .
Из (11) следует, что в этом случае, . Квадратный корень из имеет два значения. Мы можем взять любое значение. Возьмем со знаком плюс (при выборе другого значения, со знаком минус, и поменяются местами и мы не получим ничего нового):
.
Тогда
,
где – целое. Здесь мы ввели модуль и аргумент числа .
;
;
; .
Извлекаем кубический корень:
.
При , мы имеем три значения кубического корня.
По формуле (10) находим:
.
По формуле (7) имеем:
.
Полагая , мы получаем три корня приведенного уравнения:
;
;
.
Формула Виета доказана.
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Г. Корн, Справочник по математике для научных работников и инженеров, 2012.
Автор: Олег Одинцов. Опубликовано:
