Степенная функция и корни - определение, свойства и формулы

Приведены основные свойства степенной функции, включая формулы и свойства корней. Представлены производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел степенной функции.

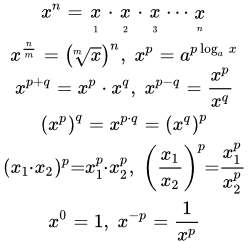
Определение

Степенная функция с показателем степени p

– это функция  f(x) = x ^p, значение которой в точке x равно значению показательной функции с основанием x в точке p.
Кроме этого,  f(0) = 0 ^p = 0  при  p > 0.

Для натуральных значений показателя , степенная функция есть произведение n чисел, равных x:
.
Она определена для всех действительных .

Для положительных рациональных значений показателя , степенная функция есть произведение n корней степени m из числа x:
.
Для нечетных m, она определена для всех действительных x. Для четных m, степенная функция определена для неотрицательных .

Для отрицательных , степенная функция определяется по формуле:
.
Поэтому она не определена в точке .

Для иррациональных значений показателя p, степенная функция определяется по формуле:
,
где a – произвольное положительное число, не равное единице:  .
При , она определена для .
При , степенная функция определена для .

Непрерывность. Степенная функция непрерывна на своей области определения.

Свойства и формулы степенной функции при x ≥ 0

Здесь мы рассмотрим свойства степенной функции при неотрицательных значениях аргумента x. Как указано выше, при некоторых значениях показателя p, степенная функция определена и для отрицательных значений x. В этом случае, ее свойства можно получить из свойств при , используя четность или нечетность. Эти случаи подробно рассмотрены и проиллюстрированы на странице «Степенная функция, ее свойства и графики».

Доказательство свойств приводится на странице «Степенная функция (доказательство непрерывности и свойств)»

Корни – определение, формулы, свойства

Корень из числа  x  степени  n

– это число   , возведение которого в степень  n  дает  x :
.
Здесь n = 2, 3, 4, ... – натуральное число, большее единицы.

Также можно сказать, что корень    из числа  x  степени  n – это корень (то есть решение) уравнения
.
Заметим, что функция является обратной к функции .

Квадратный корень из числа  x 

– это корень степени 2:  .

Кубический корень из числа  x 

– это корень степени 3:  .

Четная степень

Для четных степеней  n = 2m, корень определен при x ≥ 0. Часто используется формула, справедливая как для положительных, так и для отрицательных x:
.
Для квадратного корня:
.

Здесь важен порядок, в котором выполняются операции – то есть сначала производится возведение в квадрат, в результате чего получается неотрицательное число, а затем из него извлекается корень (из неотрицательного числа можно извлекать квадратный корень). Если бы мы изменили порядок: , то при отрицательных x корень был бы не определен, а вместе с ним не определено и все выражение.

Нечетная степень

Для нечетных степеней  , корень определен для всех x:
;
.

Свойства и формулы корней

Корень из  x  является степенной функцией:
.
При x ≥ 0 имеют место следующие формулы:
;
;
,     ;
.

Эти формулы также могут быть применимы и при отрицательных значениях переменных . Нужно только следить за тем, чтобы подкоренное выражение четных степеней не было отрицательным.

Частные значения

Корень 0 равен 0:   .
Корень 1 равен 1:   .
Квадратный корень 0 равен 0:   .
Квадратный корень 1 равен 1:   .

Пример. Корень из корней

Рассмотрим пример квадратного корня из корней:
.
Преобразуем внутренний квадратный корень, применяя приведенные выше формулы:
.
Теперь преобразуем исходный корень:
.
Итак,
.

Графики степенной функции

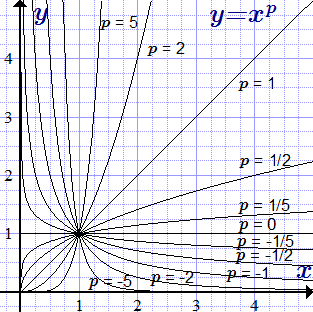
Здесь приводятся графики функции при неотрицательных значениях аргумента x. Графики степенной функции, определенной при отрицательных значениях x, приводятся на странице «Степенная функция, ее свойства и графики»

Обратная функция

Обратной для степенной функции с показателем p является степенная функция с показателем 1/p.

Если    ,   то    .

Производная степенной функции

Производная n-го порядка:
;

Вывод формул > > >

Интеграл от степенной функции

,   p ≠ – 1;
.

Разложение в степенной ряд

При   – 1 < x < 1   имеет место следующее разложение:

Выражения через комплексные числа

Рассмотрим функцию комплексного переменного z:
f(z) = z ^t.
Выразим комплексную переменную z через модуль r и аргумент φ   ( r = |z| ):
z = r e ^{i φ}.
Комплексное число t представим в виде действительной и мнимой частей:
t = p + i q.
Имеем:

Далее учтем, что аргумент φ определен не однозначно:
,

Рассмотрим случай, когда q = 0, то есть показатель степени - действительное число, t = p.   Тогда
.

Если p - целое, то и kp - целое. Тогда, в силу периодичности тригонометрических функций:
.
То есть показательная функция при целом показателе степени, для заданного z, имеет только одно значение и поэтому является однозначной.

Если p - иррациональное, то произведения kp ни при каком k не дают целого числа. Поскольку k пробегает бесконечный ряд значений k = 0, ±1, ±2, ±3, ..., то функция z ^p имеет бесконечно много значений. Всякий раз, когда аргумент z получает приращение 2 π (один оборот), мы переходим на новую ветвь функции.

Если p - рациональное, то его можно представить в виде:
, где m, n - целые, не содержащие общих делителей. Тогда
.
Первые n величин, при k = k₀ = 0, 1, 2, ... n-1, дают n различных значений kp:
.
Однако последующие величины дают значения, отличающиеся от предыдущих на целое число. Например, при k = k₀ + n имеем:
.
Тригонометрические функции, аргументы которых различаются на величины, кратные 2π, имеют равные значения. Поэтому при дальнейшем увеличении k мы получаем те же значения z ^p, что и для k = k₀ = 0, 1, 2, ... n-1.

Таким образом, показательная функция с рациональным показателем степени является многозначной и имеет n значений (ветвей). Всякий раз, когда аргумент z получает приращение 2π (один оборот), мы переходим на новую ветвь функции. Через n таких оборотов мы возвращаемся на первую ветвь, с которой начинался отсчет.

В частности, корень степени n имеет n значений. В качестве примера рассмотрим корень n – й степени действительного положительного числа z = x. В этом случае φ₀ = 0, z = r = |z| = x, .
.
Так, для квадратного корня, n = 2,
.
Для четных k, (– 1)^k = 1. Для нечетных k, (– 1)^k = – 1.
То есть квадратный корень имеет два значения:   +   и   – .

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов.     Опубликовано: 01-08-2014   Изменено: 12-12-2018