Дифференциальное уравнение Эйлера и методы его решения
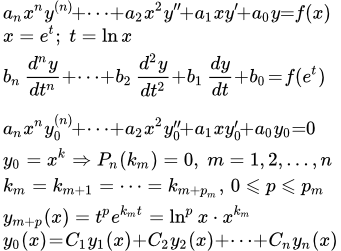
- Дифференциальное уравнение Эйлера
- – это уравнение вида
anxny(n) + an-1xn–1y(n-1) + ... + a1xy′ + a0y = f(x) .
Более общее уравнение Эйлера имеет вид:
an (ax + b ) n y (n ) + an – 1 (ax + b ) n – 1 y (n – 1 ) + ⋅ ⋅ ⋅ + a1 (ax + b ) y ′ + a0 y = f (x ) .
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.
Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.
Рассмотрим уравнение Эйлера:
(1) an x n y (n ) + an – 1 x n – 1 y (n – 1 ) + ⋅ ⋅ ⋅ + a1 xy ′ + a0 y = f (x ) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = et .
Действительно, тогда
dx = d (e t ) dt dt = e t dt ;
y ′ = dydx = dye t dt = e – t dydt ;
xy ′ = e t e – t dydt = dydt ;
y ′′ = dy ′dx = d ( e – t dydt ) e t dt = e – t ( de – t dt dydt + e – t d 2 ydt 2 ) =
e – t ( – e – t dydt + e – t d 2 ydt 2 ) = e – 2t ( d 2 ydt 2 – dydt ) ;
x 2 y ′′ = e 2t e – 2t ( d 2 ydt 2 – dydt ) = d 2 ydt 2 – dydt ;
..........................
Таким образом, множители, содержащие xm , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.
Решение однородного уравнения Эйлера
Рассмотрим однородное уравнение Эйлера:
(2) an x n y (n ) + an – 1 x n – 1 y (n – 1 ) + ⋅ ⋅ ⋅ + a1 xy ′ + a0 y = 0 .
Ищем решение уравнения (2) в виде
y = x k .
xy ′ = x (x k ) ′ = xkx k – 1 = kx k ;
x 2 y ′′ = x 2 (x k ) ′′ = x 2 k (k – 1 ) x k – 2 = k (k – 1 ) x k ;
........................
x n y (n ) = x n (x k ) (n ) = k (k – 1 ) ⋅ ⋅ ⋅(k – n + 2 ) (k – n + 1 ) x k .
Подставляем в (2) и сокращаем на xk . Получаем характеристическое уравнение:
an k (k – 1 ) ⋅ ⋅ ⋅ (k – n + 2 ) (k – n + 1 ) + an – 1 k (k – 1 ) ⋅ ⋅ ⋅(k – n + 2 ) + ⋅ ⋅ ⋅ + a1 k + a0 = 0 .
Решаем его и получаем n корней, которые могут быть комплексными.
Рассмотрим действительные корни. Пусть ki – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
yi = x ki ; yi + 1 = ln x⋅ x ki ; yi + 2 = (ln x) 2 ⋅ x ki ; ⋅ ⋅ ⋅ yi + m – 1 = (ln x) m – 1 ⋅ x ki .
Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть ki – кратный корень кратности m . Выразим комплексный корень ki через действительную и мнимую части:
ki = k1i + ik2i .
Этим m корням и m комплексно сопряженным корням соответствуют 2m линейно независимых решений:
yi = x k1i cos (k2i ln x) ; yi + 1 = x k1i sin (k2i ln x) ;
yi + 2 = ln x⋅ x k1i cos (k2i ln x) ; yi + 3 = ln x⋅ x k1i sin (k2i ln x) ;
..............................
yi + 2m – 2 = (ln x) m – 1 x k1i cos (k2i ln x) ; yi + 2m – 1 = (ln x) m – 1 x k1i sin (k2i ln x) .
После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) y = C1 y1 + C2 y2 + ⋅ ⋅ ⋅ + Cn – 1 yn – 1 + Cn yn .
Примеры
Решить уравнения:
x 3 y ′′′ + 2x 2 y ′′ – xy ′ + y = 0
x 2 y ′′ + xy ′ + y = 0
Решение примеров > > >
Решение неоднородного уравнения Эйлера
Рассмотрим неоднородное уравнение Эйлера:
an x n y (n ) + an – 1 x n – 1 y (n – 1 ) + ⋅ ⋅ ⋅ + a1 xy ′ + a0 y = f (x ) .
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.
Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные C1 , C2 ,... Cn функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные C ′i (x ) приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные C ′i (x ) . Далее находим n-ю производную y . Подставляем полученные производные y (i ) в (1) и получаем n-е уравнение, связывающее производные C ′i (x ) . Из этих уравнений определяем C ′i (x ) . После чего интегрируя, получаем общее решение уравнения (1).
Пример
Решить уравнение:
x 2 y ′′ + xy ′ – y = x(x + 1 ) 2 – ln (x + 1 )
Решение > > >
Неоднородное уравнение Эйлера со специальной неоднородной частью
Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4) an x n y (n ) + ... + a2 x 2 y ′′ + a1 xy ′ + a0 y =
x α (Ps1 (ln x) ⋅ cos (β ln x) + Qs2 (ln x) ⋅ sin (β ln x) ) ,
где Ps1 (ln x) , Qs2 (ln x) – многочлены от ln x степеней s1 и s2 , соответственно.
Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
x = e t ,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.
Автор: Олег Одинцов. Опубликовано: Изменено: