Решение линейных однородных дифференциальных уравнений с постоянными коэффициентами
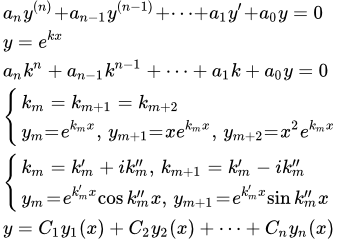
Вид общего решения
Рассмотрим линейное однородное дифференциальное уравнение с постоянными коэффициентами:
(1) an y (n ) + an – 1 y (n – 1 ) + ⋅ ⋅ ⋅ + a1 y ′ + a0 y = 0 .
Его решение можно получить следуя общему методу понижения порядка.
Однако проще сразу получить фундаментальную систему n линейно независимых решений и на ее основе составить общее решение. При этом вся процедура решения сводится к следующим шагам.
Ищем решение уравнения (1) в виде e kx . Получаем характеристическое уравнение:
(2) an k n + an – 1 k n – 1 + ⋅ ⋅ ⋅ + a1 k + a0 = 0 .
Оно имеет n корней. Решаем уравнение (2) и находим его корни km , m = 1, 2,..., n . Тогда характеристическое уравнение (2) можно представить в следующем виде:
(3) an (k – k1 ) (k – k2 ) (k – k3 ) ⋅ ⋅ ⋅ (k – kn – 1 ) (k – kn ) = 0 .
Каждому корню соответствует одно из линейно независимых решений ym (x ) фундаментальной системы решений уравнения (1). Тогда общее решение исходного уравнения (1) имеет вид:
(4) y (x ) = C1 y1 (x ) + C2 y2 (x ) + ⋅ ⋅ ⋅ + Cn – 1 yn – 1 (x ) + Cn yn (x ) .
Действительные корни
Рассмотрим действительные корни. Пусть корень km однократный. То есть множитель (k – km ) входит в характеристическое уравнение (3) только один раз. Тогда этому корню соответствует решение
ym (x ) = e km x .
Пусть km – кратный корень кратности p . То есть
km = km + 1 = ⋅ ⋅ ⋅ = km + p – 1 . В этом случае множитель (k – km ) входит в характеристическое уравнение (3) p раз:
an (k – k1 ) (k – k2 ) ⋅ ⋅ ⋅(k – km ) p ⋅ ⋅ ⋅ (k – kn – 1 ) (k – kn ) = 0 .
Этим кратным (равным) корням соответствуют p линейно независимых решений исходного уравнения (1):
ym (x ) = e km x ; ym + 1 (x ) = x e km x ; ym + 2 (x ) = x 2 e km x ; ...; ym + p – 1 (x ) = x p – 1 e km x .
Комплексные корни
Рассмотрим комплексные корни характеристического уравнения (3). Выразим комплексный корень km через действительную и мнимую части:
km = k ′m + ik ′′m .
Поскольку коэффициенты исходного уравнения (1) действительные, то кроме корня km имеется комплексно сопряженный корень
km + 1 = km = k ′m – ik ′′m .
Пусть комплексный корень km однократный. Тогда паре корней km , km + 1 = km соответствуют два линейно-независимых решения уравнения (1):
ym (x ) = e k ′mx cos (k ′′mx ) ; ym + 1 (x ) = e k ′mx sin (k ′′mx ) .
Пусть km – кратный комплексный корень кратности p . Тогда комплексно сопряженное значение km также является корнем характеристического уравнения кратности p и множитель (k – km ) (k – km ) входит в разложение на множители (3) p раз:
an (k – k1 ) (k – k2 ) ⋅ ⋅ ⋅ (k – km ) p (k – km ) p ⋅ ⋅ ⋅ (k – kn – 1 ) (k – kn ) = 0 .
Этим 2p корням соответствуют 2p линейно независимых решений:
ym (x ) = e k ′mx cos (k ′′mx ) ; ym + 1 (x ) = x e k ′mx cos (k ′′mx ) ; ym + 2 (x ) = x 2 e k ′mx cos (k ′′mx ) ; ... ym + p – 1 (x ) = x p – 1 e k ′mx cos (k ′′mx ) ;
ym + p (x ) = e k ′mx sin (k ′′mx ) ; ym + p + 1 (x ) = x e k ′mx sin (k ′′mx ) ; ym + p + 2 (x ) = x 2 e k ′mx sin (k ′′mx ) ; ... ym + 2p – 1 (x ) = x p – 1 e k ′mx sin (k ′′mx ) .
После того как фундаментальная система линейно независимых решений найдена, по формуле (4) получаем общее решение уравнения (1).
Примеры решений задач
Пример 1
Найти общее решение однородного дифференциального уравнения седьмого порядка с постоянными коэффициентами:
y (7 ) + 2y (5 ) + y ′′′ = 0 .
Решение
Ищем решение в виде e kx . Составляем характеристическое уравнение:
k 7 + 2k 5 + k 3 = 0 .
Преобразуем его:
(k 4 + 2k 2 + 1 ) k 3 = 0 ;
(k 2 + 1 ) 2 k 3 = 0 ;
(k – i ) 2 (k + i ) 2 (k – 0 ) 3 = 0 .
Рассмотрим корни этого уравнения. Мы получили четыре комплексных корня кратности 2:
k1 = k2 = i = 0 + 1 ⋅ i ; k3 = k4 = k1 = k2 = – i = 0 – 1 ⋅ i .
Им соответствуют четыре линейно-независимых решения исходного уравнения:
y1 = e 0 ⋅ x cos (1 ⋅ x ) = cos x ; y2 = x e 0 ⋅ x cos (1 ⋅ x ) = x cos x ; y3 = e 0 ⋅ x sin (1 ⋅ x ) = sin x ; y4 = x e 0 ⋅ x sin (1 ⋅ x ) = x sin x .
Также мы имеем три действительных корня кратности 3:
k5 = k6 = k7 = 0 .
Им соответствуют три линейно-независимых решения:
y5 = e 0 ⋅ x = 1 ; y6 = x e 0 ⋅ x = x ; y7 = x 2 e 0 ⋅ x = x 2 .
Общее решение исходного уравнения имеет вид:
y = C1 y1 + C2 y2 + C3 y3 + C4 y4 + C5 y5 + C6 y6 + C7 y7 .
Ответ
y = (C1 + C2 x ) cos x + (C3 + C4 x ) sin x + C5 + C6 x + C7 x 2 .
Пример 2
Решить уравнение
y ′′ + 4y ′ + 13y = 0
Решение
Это однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Ищем решение в виде e kx . Составляем характеристическое уравнение:
k 2 + 4k + 13 = 0 .
Решаем квадратное уравнение.
k = – 4 ± √ 4 2 – 4 ⋅ 13 2 = 12 (– 4 ± √ – 36 ) = 12 (– 4 ± 6i ) = – 2 ± 3i .
Мы получили два комплексных корня:
k1 = – 2 + 3i; k2 = – 2 – 3i .
Им соответствуют два линейно-независимых решения:
y1 (x ) = e – 2x cos 3x; y2 (x ) = e – 2x sin 3x .
Общее решение уравнения:
y = C1 y1 (x ) + C2 y2 (x ) = C1 e – 2x cos 3x + C2 e – 2x sin 3x .
Ответ
y = e – 2x (C1 cos 3x + C2 sin 3x ) .
Пример 3
Найти общее решение однородного дифференциального уравнения четвертого порядка с постоянными коэффициентами:
y (4 ) – 2y ′′′ + 5y ′′ = 0 .
Решение
Ищем решение в виде y = e kx . Составляем характеристическое уравнение:
k 4 – 2k 3 + 5k 2 = 0 .
Выносим k 2 за скобки:
(П3.1) k 2 (k 2 – 2k + 5 ) = 0 .
Решаем квадратное уравнение k 2 – 2k + 5 = 0 :
k = 12 ( 2 ± √ (– 2 ) 2 – 4 ⋅ 5 ) = 12 ( 2 ± √ – 16 ) = 12 (2 ± 4i ) = 1 ± 2i .
Получили два комплексных корня, которые обозначим как k3 = 1 + 2i, k4 = 1 – 2i . Тогда k 2 – 2k + 5 = (k – k3 ) (k – k4 ) = (k – 1 – 2i ) (k – 1 + 2i ) . Перепишем характеристическое уравнение (П3.1) в эквивалентном виде:
(k – 0 ) (k – 0 ) (k – 1 – 2i ) (k – 1 + 2i ) = 0 .
Отсюда видно, что оно имеет два кратных корня k1 = k2 = 0 кратности 2, и два комплексно сопряженных корня k3 = 1 + 2i, k4 = 1 – 2i . Кратным корням k1 = k2 = 0 соответствуют два линейно независимых решения:
y1 (x ) = e k1 x = e 0 ⋅ x = 1 ;
y2 (x ) = xe k1 x = xe 0 ⋅ x = x .
Комплексно сопряженным корням k3 = 1 + 2i; k4 = 1 – 2i , соответствуют решения
y3 (x ) = e 1 ⋅ x cos 2x = e x cos 2x; y4 (x ) = e 1 ⋅ x sin 2x = e x sin 2x .
Общее решение:
y = C1 y1 (x ) + C2 y2 (x ) + C3 y3 (x ) + C4 y4 (x ) = C1 + C2 x + C3 e x cos 2x + C4 e x sin 2x .
Ответ
y = C1 + C2 x + e x (C3 cos 2x + C4 sin 2x ) .
Пример 4
Найдите однородное линейное дифференциальное уравнение с постоянными коэффициентами, для которого данные функции являются частными решениями:
y1 = x 2 , y2 = e x cos 3x .
Решение
Фундаментальную систему решений линейного однородного уравнения с постоянными коэффициентами можно представить в виде множества функций вида
x pj e km x , pj = 0, 1, 2, . . ., pm ,
где km – корень характеристического уравнения кратности pm + 1 .
Запишем заданные частные решения в виде суммы произведений многочленов на экспоненту вида e kx :
y1 = x 2 = x 2 e 0 ⋅ x ;
y2 = e x cos 3x = 12 e x ( e i3x + e – i3x ) = 12 e (1 + 3i ) x + 12 e (1 – 3i ) x =
12 x 0 e (1 + 3i ) x + 12 x 0 e (1 – 3i ) x .
Поскольку любое решение уравнения линейно выражается через решения фундаментальной системы, то в нее должны входить следующие функции:
x 2 e 0 ⋅ x , x 0 e (1 + 3i ) x , x 0 e (1 – 3i ) x .
Поэтому характеристическое уравнение должно иметь следующие корни:
k1 = 0 кратности p1 + 1 = 2 + 1 = 3 ;
k2 = 1 + 3i кратности p2 + 1 = 0 + 1 = 1 ;
k3 = 1 – 3i кратности p3 + 1 = 0 + 1 = 1 .
Характеристическое уравнение наименьшего порядка с такими корнями имеет следующий вид:
(k – k1 ) p1 + 1 ⋅ (k – k2 ) p2 + 1 ⋅ (k – k3 ) p3 + 1 = 0 ;
(k – 0 ) 3 ⋅ (k – (1 + 3i ) ) 1 ⋅ (k – (1 – 3i ) ) 1 = 0 ;
k 3 (k – (1 + 3i ) ) (k – (1 – 3i ) ) = 0 ;
k 3 (k 2 – k (1 – 3i ) – (1 + 3i ) k + (1 + 3i ) (1 – 3i ) ) = 0 ;
k 3 (k 2 – 2k + 1 – 3i + 3i (1 – 3i ) ) = 0 ;
k 3 (k 2 – 2k + 1 + 9 ) = 0 ;
k 3 (k 2 – 2k + 10 ) = 0 ;
k 5 – 2k 4 + 10k 3 = 0 .
Такому характеристическому уравнению соответствует следующее дифференциальное уравнение:
y V – 2y IV + 10y ′′′ = 0 .
Ответ
y V – 2y IV + 10y ′′′ = 0 .
Автор: Олег Одинцов. Опубликовано: Изменено: