Решение дифференциальных уравнений высших порядков методом Бернулли
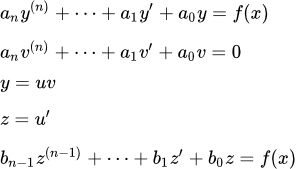
Метод решения
Ранее мы рассмотрели метод Бернулли для решения линейных неоднородных дифференциальных уравнений первого порядка. Этот метод также можно применить и для решения уравнений высших порядков. Если нам известно частное решение однородного уравнения, то применяя метод Бернулли, мы можем понизить порядок уравнения.
Пусть мы имеем линейное неоднородное дифференциальное уравнение произвольного, n-го порядка:
(1) .
Здесь является функцией от независимой переменной x. Коэффициенты также являются функциями от x.
.
Пусть функция есть частное (любое, отличное от нуля) решение однородного уравнения
(2) .
Тогда подстановка
приводит к понижению порядка исходного уравнения (1). Здесь – функция от переменной x.
Пусть нам известна функция , удовлетворяющая уравнению (2). Применим формулу Лейбница для n-й производной произведения двух функций:
.
Здесь – биномиальные коэффициенты.
Разобьем сумму на две части:
.
Тогда первая часть содержит только производные от неизвестной функции u. Подставим в (1) и сгруппируем члены:
.
В силу (2), сумма членов в скобках равна нулю. В результате получаем:
.
Это линейное неоднородное дифференциальное уравнение n-го порядка относительно неизвестной функции . Оно содержит производные функции u и не содержит саму функцию в явном виде. Выполнив подстановку , мы получим линейное неоднородное уравнение n-1 -го порядка.
См. «Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде».
Пример 1
Решить дифференциальное уравнение с постоянными коэффициентами второго порядка методом Бернулли (введением двух функций):
(П1.1)
Решение
Шаг 1. Вводим две функции
Ищем решение в виде произведения двух функций:
(П1.2) .
Подставляем в уравнение (П1.1) и группируем члены:
;
(П1.3) .
Шаг 2. Решение однородного уравнения
Решаем однородное уравнение
(П1.4) .
Ищем решение в виде . Получаем характеристическое уравнение:
.
Решаем квадратное уравнение:
.
Получаем кратные корни: . Этим корням соответствуют два линейно-независимых решения линейного однородного уравнения (П1.4):
.
В качестве функции мы можем взять любое решение уравнения (П1.4). Возьмем наиболее простое. Пусть
(П1.5) .
Шаг 3. Понижение порядка
Подставляем (П1.5) в (П1.3), учитывая (П1.4):
;
;
;
;
(П1.6) .
Шаг 4. Интегрирование
Интегрируем (П1.6), используя таблицу интегралов:
;
;
.
Окончательно имеем:
.
Ответ
.
Пример 2
Решить дифференциальное уравнение второго порядка методом Бернулли:
(П2.1)
Решение
Шаг 1. Вводим две функции
Ищем решение в виде произведения двух функций:
(П2.2) .
Подставляем в уравнение (П2.1) и группируем члены:
;
(П2.3) .
Шаг 2. Решение однородного уравнения
Решаем однородное уравнение
(П2.4) .
Ищем решение в виде . Получаем характеристическое уравнение:
.
Оно имеет комплексные корни:
.
Этим корням соответствуют два линейно-независимых решения однородного уравнения (П2.4):
.
В качестве функции , мы можем взять любое, отличное от нуля, решение уравнения (П2.4). Возьмем
(П2.5) .
Шаг 3. Понижение порядка
Подставляем (П2.5) в (П2.3), учитывая (П2.4):
;
;
.
Мы получили дифференциальное уравнение, не содержащее функцию в явном виде. Сделаем подстановку . В результате получаем линейное дифференциальное уравнение первого порядка:
(П2.6) .
Шаг 4. Решение дифференциального уравнения первого порядка
Уравнение (П2.6) можно также решить методом Бернулли, но это проще сделать с помощью интегрирующего множителя. Умножим уравнение (П2.6) на и выполняем преобразования:
;
;
.
Интегрируем:
.
Возвращаемся к переменной u:
.
Интегрируем еще раз и вычисляем интегралы (см. «Интегрирование тригонометрических рациональных функций» и «Таблица неопределенных интегралов»):
;
;
;
.
Окончательно имеем:
.
Ответ
.
Автор: Олег Одинцов. Опубликовано:
