Пример решения неоднородного дифференциального уравнения Эйлера второго порядка

Рассмотрен пример решения неоднородного дифференциального уравнения Эйлера второго порядка методом вариации постоянных Лагранжа.

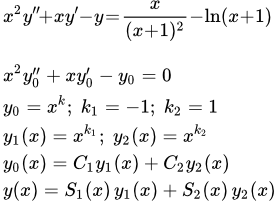
Здесь мы рассматриваем пример решения неоднородного дифференциального уравнения Эйлера. Методы решения уравнения Эйлера подробно рассмотрены на странице
“Дифференциальное уравнение Эйлера и методы его решения > > >”.

Пример

Решить дифференциальное уравнение Эйлера второго порядка
(1)   .

Решение

Ищем общее решение однородного уравнения второго порядка:
(2)   .
Ищем решение в виде
. Тогда
;
.

Подставляем в (2):
.
Сокращаем на x^k и получаем характеристическое уравнение второго порядка:
.
Преобразуем.
;
;
.
Получили два действительных корня:
.
Им соответствуют два линейно независимых решения:
(3)   .
Общее решение уравнения:
(4)   .

Далее считаем, что постоянные C₁ и C₂ являются функциями от x. Находим производные.
.
Положим
(5)   .
Тогда
;
.
Подставим в (1):
(1)   ;



.
Поскольку функции и удовлетворяют уравнению (2), то часть членов сокращается. Остается:
.
Таким образом, вместе с (5) мы получили систему уравнений:
.
.

Подставляем:
.
;
;
.

Из второго:
.
Подставим в первое:
.
Интегрируем:
.
Здесь – постоянная интегрирования.
Интегрируем по частям:

.
Подставляем:
;

;
.

Находим .
;




.

Итак, мы нашли:
;
.
Общее решение:



;
;
.
Переобозначив постоянные, окончательно имеем.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 14-08-2013