Пример решения линейного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью

Рассмотрен пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью в виде суммы экспоненты, умноженной на x, синуса и многочлена второй степени.

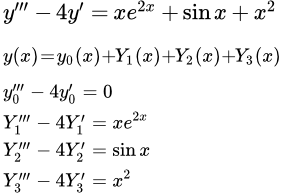
Здесь мы рассмотрим пример решения линейного дифференциального уравнения со специальной неоднородной частью. Метод решения таких уравнений подробно рассмотрен на странице «Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью».

Пример

Решить уравнение:
.

Решение

Общее решение однородного уравнения

Вначале находим общее решение однородного дифференциального уравнения
.
Ищем решение в виде . Составляем характеристическое уравнение:
.
Преобразуем его.
;
.
Получили три действительных корня:
.
Им соответствуют три решения фундаментальной системы решений:
.
Общее решение однородного уравнения:
.

Ищем частное решение неоднородного уравнения. Для этого неоднородную часть представим в виде суммы трех частей:
.

Частное решение с первой неоднородностью

Ищем частное решение дифференциального уравнения с первой неоднородной частью.
(П1)   .
Неоднородность имеет вид многочлена первой степени, умноженного на экспоненту:
.
Характеристическое уравнение имеет корень , кратности . Тогда частное решение имеет вид многочлена первой степени, умноженного на и на экспоненту:
.
Находим производные.
;

;


;


.
Подставляем в (П1):

.
Сокращаем на и преобразуем:
.
Отсюда:

;
.

Частное решение со второй неоднородностью

Ищем частное решение со второй неоднородной частью:
(П2)   .
Неоднородность имеет вид суммы произведений многочленов степени 0 (то есть постоянных), умноженных на косинус и синус:

.
Поскольку характеристическое уравнение не имеет комплексного корня , то частное решение имеет вид суммы произведений многочленов степеней 0 (то есть постоянных), умноженных на косинус и синус:
.
Находим производные.
;
;
;
.
Подставляем в (П2):
.
Преобразуем:
.
Отсюда

;
.

Частное решение с третьей неоднородностью

Ищем частное решение дифференциального уравнения с третьей неоднородной частью:
(П3)   .
Здесь неоднородная часть является многочленом второй степени. Ему соответствует . Правую часть можно записать в стандартном виде так:
.
Поскольку характеристическое уравнение имеет однократный корень , то частное решение имеет вид многочлена второй степени, умноженного на (здесь p = 1 – кратность корня ):
.
Находим производные:
;
;
.
Подставляем в (П3):
.
Преобразуем:
.
Отсюда

;
.

Общее решение исходного уравнения:
.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 30-07-2013   Изменено: 15-10-2020