Методы решения пределов функций в картинках
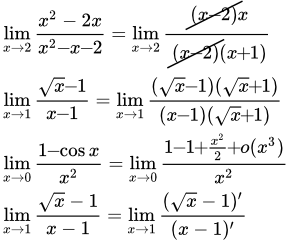
Приводятся методы, применяемые при вычислении пределов функций в сжатом виде – в виде изображений. Каждая картинка содержит основные формулы и понятия страницы, к которой она относится. Картинки сопровождаются заголовками, описаниями страниц и ссылками на них.
Здесь приводится содержание раздела «Методы вычисления пределов» в картинках. На изображениях, в кратком виде представлено содержание страниц раздела. На многих из них излагаются методы, применяемые при вычислении пределов. Рядом с каждым изображением имеется заголовок, описание страницы и ссылка на нее. Просматривая их, можно освежить в памяти применяемые методы и некоторые формулы, а также перейти на страницу с подробным изложением материала.
Методы вычисления пределов функций и раскрытия неопределенностей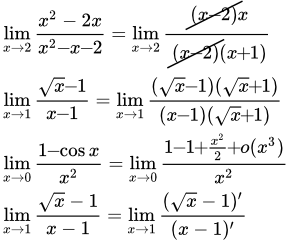Изложены приемы и методы решения задач на вычисление пределов и раскрытие неопределенностей. Рассмотрены следующие вопросы: пределы с непрерывными и сложными функциями; известные пределы; сведение неопределенности одного вида к другому; раскрытие неопределенностей с дробями из многочленов и корней; сравнение функций и решение разложением в степенной ряд; правило Лопиталя. Примеры пределов с решениями
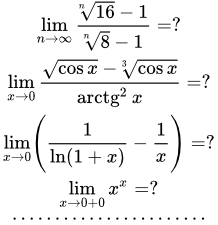Страница содержит ссылки на 45 примеров решений пределов функций и 24 задачи на смежные темы. К смежным темам относятся задачи на применение определений предела последовательности и предела функции, а также задачи на непрерывность функции. Замена переменной при решении пределов
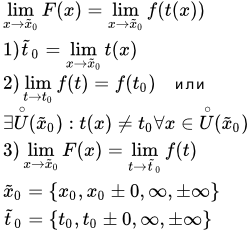Изложены правила, которые необходимо соблюдать, применяя замену переменной при решении пределов. Формальное применение подстановок, в некоторых случаях, может приводить к неверному результату. Приводится пример, в котором существуют промежуточные пределы, но предела исходной сложной функции не существует. Решение пределов с дробями из многочленов
Изложены приемы и методы решения пределов дробей с отношениями многочленов. Рассмотрены неопределенности вида ∞ / ∞, 0 / 0 и ∞ ± ∞. Разобраны случаи, когда переменная стремится к бесконечности и к конечному числу. Для каждого варианта приводятся примеры с подробными объяснениями и ссылками на применяемые теоремы и свойства. Решение пределов с корнями
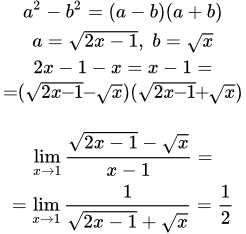Изложены методы решения задач на вычисление пределов и раскрытие неопределенностей от функций с корнями. Рассмотрены следующие приемы: применение подстановки; применение формул разности квадратов (и других степеней) для линеаризации бесконечно малой части; деление числителя и знаменателя дроби на степенную функцию. Приводятся примеры с подробными решениями. Доказательство первого замечательного предела и его следствий
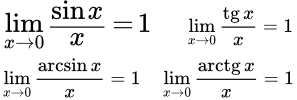Приводится доказательство первого замечательного предела и его следствий. Дается определение длины дуги окружности как верхней грани множества длин ломаных, вписанных в дугу. 
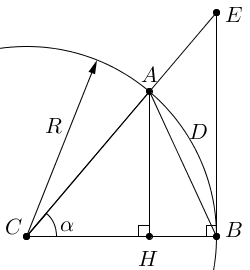Доказательство первого замечательного предела:
SCAB < SCADB < SCEB.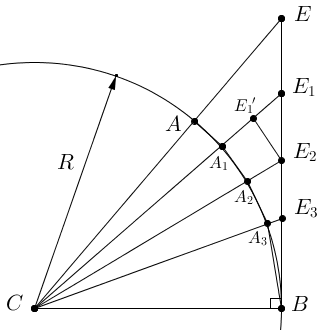
Длина ломаной, вписанной в дугу AB, меньше длины отрезка |BE|. 
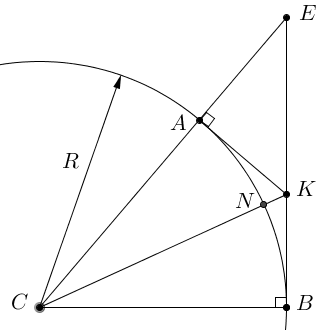Длина дуги окружности AB меньше длины отрезка EB. Примеры решений задач с помощью первого замечательного предела
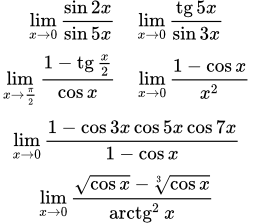Собраны формулы, свойства и теоремы, применяемые при решении задач, допускающих решение с помощью первого замечательного предела. Даны подробные решения примеров с использованием первого замечательного предела и его следствий. Доказательство второго замечательного предела и его следствий
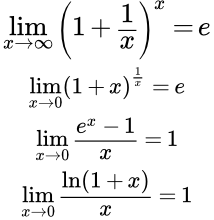Приводится доказательство второго замечательного предела и его следствий. Примеры решений задач с помощью второго замечательного предела
Подробные решения примеров с использованием второго замечательного предела и его следствий. Формулы, свойства и теоремы, применяемые при решении задач, допускающих решение с помощью второго замечательного предела. О большое и о малое. Сравнение функций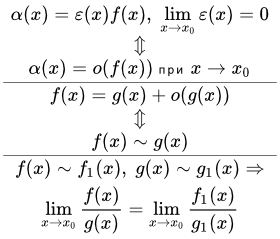
Даны определения о малого, о большого, эквивалентных (асимптотически равных) функций, функций одного порядка, и их свойства. Приводятся доказательства свойств и теорем. Эти свойства и теоремы используются для сравнения функций и вычисления пределов при аргументе, стремящемся к конечной или бесконечно удаленной точке. Решение пределов, используя ряд Тейлора
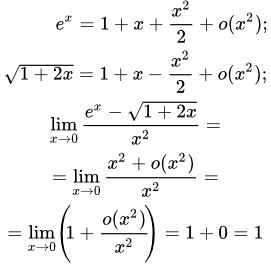Изложен метод решения пределов, используя разложение функций в ряд Тейлора. Приводятся применяемые в этом методе свойства о малого и разложения элементарных функций в ряд Маклорена. Подробно разобраны примеры решения пределов, содержащих неопределенности ∞ – ∞, один в степени бесконечность и 0/0. Решение пределов функций, используя правило Лопиталя
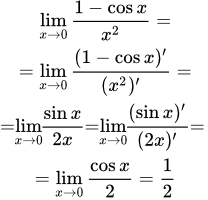Изложен метод решения пределов, используя правило Лопиталя. Приводятся формулировки соответствующих теорем. Подробно разобраны примеры решения пределов, содержащих неопределенности ∞/∞, 0/0, 0 в степени 0 и ∞ – ∞, с помощью правила Лопиталя. Применение эквивалентных функций при решении пределов
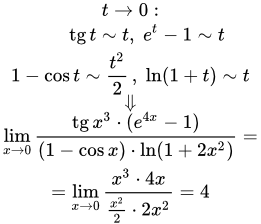Изложен метод, позволяющий упростить вычисление пределов, применяя эквивалентные функции. Этот метод применим при вычислении пределов дробей с множителями в числителе или знаменателе. Дана таблица эквивалентных функций при x→0. Приводятся подробно разобранные примеры применения этого метода.
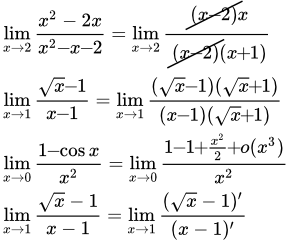Изложены приемы и методы решения задач на вычисление пределов и раскрытие неопределенностей. Рассмотрены следующие вопросы: пределы с непрерывными и сложными функциями; известные пределы; сведение неопределенности одного вида к другому; раскрытие неопределенностей с дробями из многочленов и корней; сравнение функций и решение разложением в степенной ряд; правило Лопиталя. Примеры пределов с решениями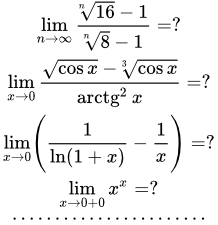Страница содержит ссылки на 45 примеров решений пределов функций и 24 задачи на смежные темы. К смежным темам относятся задачи на применение определений предела последовательности и предела функции, а также задачи на непрерывность функции. Замена переменной при решении пределов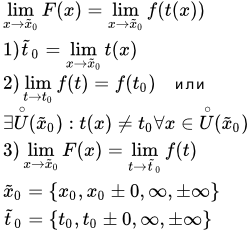Изложены правила, которые необходимо соблюдать, применяя замену переменной при решении пределов. Формальное применение подстановок, в некоторых случаях, может приводить к неверному результату. Приводится пример, в котором существуют промежуточные пределы, но предела исходной сложной функции не существует. Решение пределов с дробями из многочленовИзложены приемы и методы решения пределов дробей с отношениями многочленов. Рассмотрены неопределенности вида ∞ / ∞, 0 / 0 и ∞ ± ∞. Разобраны случаи, когда переменная стремится к бесконечности и к конечному числу. Для каждого варианта приводятся примеры с подробными объяснениями и ссылками на применяемые теоремы и свойства. 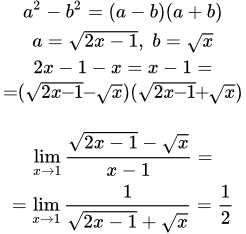Решение пределов с корнямиИзложены методы решения задач на вычисление пределов и раскрытие неопределенностей от функций с корнями. Рассмотрены следующие приемы: применение подстановки; применение формул разности квадратов (и других степеней) для линеаризации бесконечно малой части; деление числителя и знаменателя дроби на степенную функцию. Приводятся примеры с подробными решениями. Доказательство первого замечательного предела и его следствий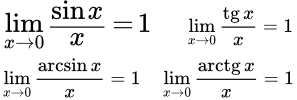Приводится доказательство первого замечательного предела и его следствий. Дается определение длины дуги окружности как верхней грани множества длин ломаных, вписанных в дугу. Доказательство первого замечательного предела:SCAB < SCADB < SCEB.
Длина ломаной, вписанной в дугу AB, меньше длины отрезка |BE|. Длина дуги окружности AB меньше длины отрезка EB. Примеры решений задач с помощью первого замечательного предела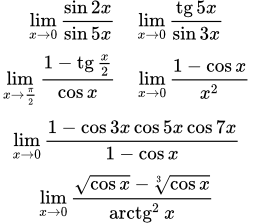Собраны формулы, свойства и теоремы, применяемые при решении задач, допускающих решение с помощью первого замечательного предела. Даны подробные решения примеров с использованием первого замечательного предела и его следствий. Доказательство второго замечательного предела и его следствий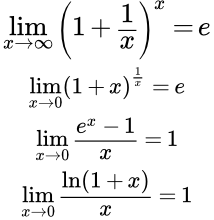Приводится доказательство второго замечательного предела и его следствий. Примеры решений задач с помощью второго замечательного пределаПодробные решения примеров с использованием второго замечательного предела и его следствий. Формулы, свойства и теоремы, применяемые при решении задач, допускающих решение с помощью второго замечательного предела. О большое и о малое. Сравнение функций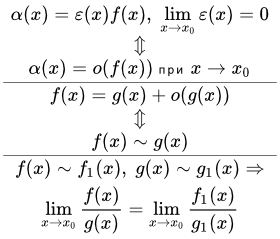Даны определения о малого, о большого, эквивалентных (асимптотически равных) функций, функций одного порядка, и их свойства. Приводятся доказательства свойств и теорем. Эти свойства и теоремы используются для сравнения функций и вычисления пределов при аргументе, стремящемся к конечной или бесконечно удаленной точке. Решение пределов, используя ряд Тейлора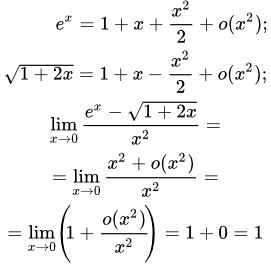Изложен метод решения пределов, используя разложение функций в ряд Тейлора. Приводятся применяемые в этом методе свойства о малого и разложения элементарных функций в ряд Маклорена. Подробно разобраны примеры решения пределов, содержащих неопределенности ∞ – ∞, один в степени бесконечность и 0/0. Решение пределов функций, используя правило Лопиталя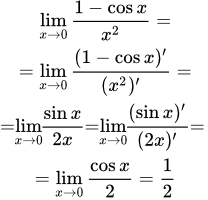Изложен метод решения пределов, используя правило Лопиталя. Приводятся формулировки соответствующих теорем. Подробно разобраны примеры решения пределов, содержащих неопределенности ∞/∞, 0/0, 0 в степени 0 и ∞ – ∞, с помощью правила Лопиталя. Применение эквивалентных функций при решении пределов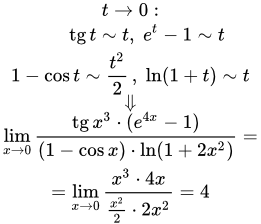Изложен метод, позволяющий упростить вычисление пределов, применяя эквивалентные функции. Этот метод применим при вычислении пределов дробей с множителями в числителе или знаменателе. Дана таблица эквивалентных функций при x→0. Приводятся подробно разобранные примеры применения этого метода.