Дифференциальное уравнение y(n) = f(x)
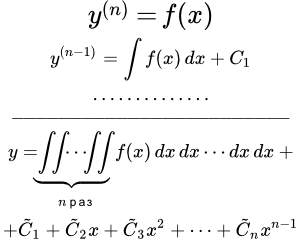
Общее решение
Рассмотрим дифференциальное уравнение n-го порядка, в котором n-я производная равна функции от независимой переменной x:
(1) .
Оно решается непосредственным интегрированием.
;
;
;
;
;
;
. . . . . . . .
.
Заменим постоянные интегрирования:
.
Тогда
(2) .
В результате мы получили общее решение (2) уравнения (1). Оно представляет собой сумму n-кратного повторного интеграла и многочлена степени .
Таким образом, если нас интересует общее решение уравнения (1), то мы должны проинтегрировать функцию n раз, и прибавить многочлен степени , коэффициентами которого являются постоянные интегрирования.
Частное решение с заданными начальными условиями
Если нас интересует задача Коши с заданными начальными условиями
(3) ,
то соответствующее частное решение имеет следующий вид:
(4)
.
См. «Решение дифференциального уравнения y(n)=f(x) с заданными начальными условиями».
Применение формулы Коши для повторных интегралов
Входящий в (4) n-кратный интеграл можно свести к однократному, если воспользоваться формулой Коши для повторных интегралов:
(5) .
Тогда решение уравнения (1) с начальными условиями (3) примет более простой вид:
(6)
.
Вывод формулы Коши (5) изложен на странице «Формула Коши для повторных интегралов». Здесь мы покажем, что функция , определяемое по формуле (6), удовлетворяет дифференциальному уравнению (1).
Дифференцируем (6):
.
Выполняя n – 1 дифференцирований, получаем:
.
Дифференцируя еще раз, приходим к уравнению (1):
.
Пример
Найти общее решение уравнения:
.
Решение
Разделим исходное уравнение на . При получаем уравнение вида (1):
.
Преобразуем, применяя формулу тригонометрии:
.
Интегрируем:
.
Интегрируем еще два раза:
;
.
Преобразуем постоянные интегрирования:
.
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
