Интегрирование тригонометрических рациональных функций
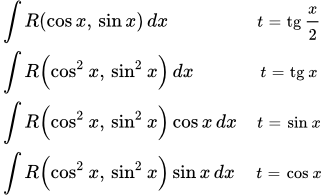
Методы интегрирования тригонометрических рациональных функций
Рассмотрим интегралы от тригонометрических рациональных функций:
,
где R – рациональная функция, то есть функция, составленная из операций сложения, деления и возведения в целочисленную степень. Сюда также могут входить тангенсы и котангенсы (поскольку они получаются операциями деления синуса и косинуса). Их, чаще всего, стоит преобразовать через синусы и косинусы.
В зависимости от вида подынтегральной функции, применяют несколько методов интегрирования тригонометрических рациональных функций.
Подстановки t = sin x или t = cos x
Если R( cos x, sin x ) умножается на –1 при замене
cos x → – cos x или sin x → – sin x ,
то полезно другую из них обозначить через t.
Так, при подстановке
t = cos x ,
dt = (cos x )′ dx = – sin x dx,
sin2 x = 1 – cos2 x = 1 – t 2.
При подстановке
t = sin x ,
dt = (sin x )′ dx = cos x dx,
cos2 x = 1 – sin2 x = 1 – t 2.
Подстановка t = tg x
Если R( cos x, sin x ) не меняется при одновременной замене
cos x → – cos x и sin x → – sin x ,
то полезно положить tg x = t или ctg x = t.
Пусть t = tg x, тогда
,
,
,
.
Подстановка t = tg(x/2)
Подстановка
во всех случаях приводит к интегралу от рациональной дроби.
При этом
,
,
,
,
,
.
Итак,
.
Эта подстановка является универсальной и позволяет во всех случаях привести интегралы от тригонометрических рациональных функций к интегралам от рациональных функций. К сожалению, эта подстановка приводит к более длинным вычислениям, чем предыдущие, если они применимы.
Интегралы с произведением степенных функций от cos x и sin x
Часто встречаются интегралы, в которых подынтегральная функция является произведением степенных функций от синуса и косинуса:
При целых m и n подынтегральная функция является тригонометрической рациональной функцией и, для ее интегрирования, применимы перечисленные выше методы. Однако, в виду особенности, существует ряд дополнительных методов, которые, в некоторых случаях, позволяют упростить вычисление таких интегралов.
Подробнее >>>
Примеры
Ниже подробно рассмотрены три примера интегрирования рациональных тригонометрических функций.
Пример 1
Вычислить интеграл
Решение
Подынтегральная функция
является дробью, состоящей из многочленов от тригонометрических функций sin x и cos x. Поэтому она является рациональной функцией от sin x и cos x.
Заменим cos x на – cos x:
Вся функция умножилась на –1 .
По правилу 1, делаем подстановку:
t = sin x.
Тогда
dt = (sin x)′ dx = cos x dx.
Подставляем в интеграл:
Получили интеграл от рациональной функции (дроби из многочленов). Выделяем целую часть и разложим дробь на простейшие:
.
Интегрируем:
Ответ
Пример 2
Определить интеграл
Решение
Подынтегральная функция
является дробью, состоящей из многочленов от тригонометрической функции sin x. Поэтому она является рациональной функцией от sin x и cos x.
Заменим sin x на – sin x:
Функция не изменилась.
Заменим cos x на – cos x. Поскольку подынтегральная функция не зависит от cos x, то при этой замене она также не меняется.
Согласно второму правилу, приведенному выше, делаем подстановку:
t = tg x.
;
;
.
Применим формулу sin2 x + cos2 x = 1 и разделим числитель и знаменатель на cos2 x.
.
Подставляем и раскладываем дробь на простейшие:
.
Ответ
Пример 3
Решить интеграл
Решение
Подынтегральная функция
является дробью, состоящей из многочлена от тригонометрических функций sin x и cos x. Поэтому она является рациональной функцией от sin x и cos x.
Если заменить sin x на – sin x или cos x на – cos x, то функция меняет вид, поэтому правила 1 или 2 не применимы.
Согласно третьему правилу, приведенному выше, делаем подстановку:
.
;
.
Преобразуем знаменатель, применяя формулы:
,
,
.
.
.
Приводим знаменатель к сумме квадратов:
.
Подставляем:
Ответ
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано:
