Дифференциальные уравнения, допускающие понижение порядка

Перечислены типы дифференциальных уравнений, допускающие понижение порядка, и указаны методы их решений. Рассмотрены примеры понижения порядка и решения таких уравнений.

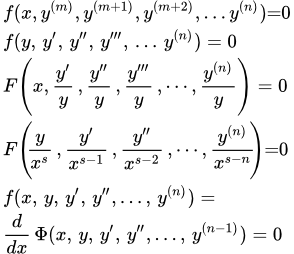
Уравнения, не содержащие зависимую переменную y в явном виде

, или
Если дифференциальное уравнение не содержит зависимую переменную в явном виде, то после подстановки , порядок уравнения понижается на единицу. Если уравнение не содержит также и несколько ее первых производных, то делаем подстановку , где m – наименьший порядок производной функции , входящей в уравнение. В результате порядок уравнения понижается на m.

Примеры с решениями:    

Уравнения, не содержащие независимую переменную x в явном виде

В таких уравнениях порядок понижается на единицу, если за независимую переменную принять , а в качестве зависимой взять . То есть выполнить подстановку
,
где – функция, зависящая от . Тогда
.

Примеры с решениями:    

Уравнения, однородные относительно функции и ее производных

Это дифференциальное уравнение, однородное относительно зависимой переменной и всех ее производных. Чтобы распознать такое уравнение, нужно сделать замены
.
Если после преобразований сократится, то это однородное уравнение.

В таком уравнении можно понизить порядок, если сделать подстановку
,
где – функция от .

Примеры с решениями:    

Обобщенно однородные уравнения относительно переменных

Обобщенно однородные дифференциальные уравнения высших порядков не меняют вида, если сделать замену переменных: , где t – постоянная; s – число, измерение однородности для переменной y. При такой замене производная порядка m умножается на :
.
При подобные уравнения можно назвать однородными дифференциальными уравнениями относительно переменных.

Чтобы распознать такое уравнение, нужно сделать замены
.
Если удастся подобрать такое число s, в результате чего t сократится, то это обобщенно однородное уравнение относительно переменных.

Порядок такого уравнения можно понизить на единицу, если искать решение в параметрическом виде, и перейти от зависимой переменной (функции) y к новой зависимой переменной с помощью подстановок:
при ;
при ;
где t – новая независимая переменная.
В результате для функции получим дифференциальное уравнение n - го порядка, которое не содержит переменную t в явном виде. Далее понижаем порядок изложенным выше методом ⇑.

Примеры с решениями:    

Дифференциальные уравнения с полной производной

Это уравнения, которые можно привести к полной производной:
.
Отсюда получаем первый интеграл:
.
Он представляет собой дифференциальное уравнение, порядок которого на единицу меньше порядка исходного уравнения.

Примеры с решениями:            

Примеры решений задач на понижение порядка дифференциальных уравнений

Ниже собраны примеры решений дифференциальных уравнений высших порядков, решаемых понижением порядка.
                                           

Пример. Уравнение без y и y′

Найти общее решение дифференциального уравнения третьего порядка.
.

Решение

Здесь дифференциальное уравнение третьего порядка не содержит и первую производную в явном виде. Поэтому делаем подстановку . Тогда . Подставляем в уравнение и решаем его.
;
;   ;
;
;
;
;
;
;
;
;
;

;
.

Ответ

.

Пример. Уравнение без x

.

Решение

Это дифференциальное уравнение второго порядка; оно не содержит явно независимую переменную x. Чтобы понизить порядок, примем за независимую переменную, а – за зависимую. Делаем подстановку ,
где . Тогда
.
Подставляем в исходное уравнение:
.
Мы получили уравнение первого порядка для функции . Решаем его.
;
;
;
;
;
;
;
;
;
;
;
;
;
.

Ответ

.

Пример. Уравнение, однородное относительно y

.

Решение

Пример. В качестве примера рассмотрим предыдущее уравнение
,
но будем его решать другим способом.

Убедимся, что это однородное уравнение. Для этого делаем замены: ;
;
;
.
сократилось. Значит это дифференциальное уравнение второго порядка, однородное относительно функции и ее производных.

Делаем подстановку , где – функция от независимой переменной .
.
Подставляем в исходное уравнение.
;
;
;
;
.
.
Мы получили дифференциальное уравнение первого порядка для функции . Получилось простейшее уравнение. Его решением является постоянная:
.
Находим .
;
;
;
;
;
;
;
;
.

Ответ

.

Пример. Уравнение, однородное относительно x и y

Решить дифференциальное уравнение, удовлетворяющее заданным условиям Коши.
.

Решение

Исследуем, является ли это уравнение обобщенно однородным относительно переменных. Делаем замены:
:
;
.
Чтобы t сократилось, должны выполняться условия:
;
.
Отсюда . То есть это уравнение является обобщенно однородным относительно переменных с измерением однородности .

Делаем подстановки:
, где t – независимая переменная; – зависимая переменная, функция от t.
;
;
;
.
Напомним, что знак штрих «′» означает производную по аргументу функции: для функции это производная по переменной x; для это производная по переменной t.

Подставляем в исходное уравнение.
;
;
;
;
(П4.1)   .
Это уравнение не содержит явно независимую переменную t. Понижаем порядок. Для этого в качестве независимой переменной возьмем u. Вводим новую переменную , которая обозначает функцию от u: . Тогда
.
Подставляем в (П4.1) и решаем уравнение.
;
;
;
;
;
(П4.2)   .

Определим постоянную из начальных условий . При ;
;
.
Подставляем в (П4.2) :
;
.

Решаем (П4.2) с найденным значением постоянной .
;
;
;
(П4.3)   ;

Определяем постоянную из начальных условий, подставляя :
;
.

Подставляя в (П4.3), получаем решение исходного уравнения.
;
;
;
.
Исключаем переменную , подставляя .

Ответ

.

Пример. Уравнение с полной производной

Решить дифференциальное уравнение, удовлетворяющее заданным условиям.
.

Решение

Замечаем, что . Тогда
.
Отсюда получаем интеграл, в котором порядок уравнения понизился на единицу:
(П5.1)   .
Определим значение постоянной из начальных условий, подставляя :
.
Отсюда . Подставляем в (П5.1) и разделяем переменные.
;
;
;
;
;
;
.
Подставляя из начальных условий , находим постоянную :
;
.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 17-08-2024