Примеры как найти дифференциал функции

Подробно разобраны примеры вычислений дифференциала функции первого, второго и третьего порядков. Показано как вычислять дифференциалы высших порядков с помощью подстановки. Разобран пример нахождения приближенного значения функции с оценкой погрешности вычисления. Приводятся основные формулы, используемые при решении примеров.

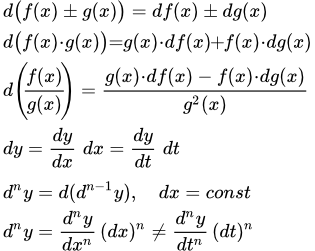
Здесь мы рассмотрим примеры вычислений дифференциалов функций и связанные с этим задачи. В конце приводятся определения и основные свойства дифференциалов, применяемые при решении задач.
Ниже рассмотрены следующие примеры. Найти приращение и дифференциал функции в точке x.
. Найти дифференциал функции
. Найти дифференциалы первого, второго и третьего порядков функции
. С помощью дифференциала вычислить приближенное значение .

Пример 1. Вычисление приращения и дифференциала функции

Найти приращение и через него дифференциал функции в точке x.
.

Решение

Найдем приращение заданной функции в точке x.


;
.

Линейная часть этого приращения по является дифференциалом функции.
.
Заметим, что этот результат можно получить, если найти производную и применить формулу .

Ответ

Приращение функции:
.
Дифференциал:
.

Пример 2. Найти дифференциал функции

Найти дифференциал функции в точке x.
.

Решение

Можно сначала найти производную , и применить формулу . Но мы произведем вычисления, применяя свойства дифференциалов.

Здесь удобно вычислять с конца.
Применим формулу .
;
.
Выносим постоянную за знак дифференциала.
.
Дифференциал постоянной равен нулю.
.
Вводим переменную , и применяем формулу дифференциала суммы и разности.
.
Используем инвариантность первого дифференциала, и вычисляем более простой дифференциал от переменной t. Затем переходим к переменной x

;
.
Вычисляем дифференциал произведения.

;
.

Аналогичным образом находим дифференциал второго слагаемого, вводя переменную
.
;

;
.

Применяя формулу дифференциала суммы, находим первый дифференциал.

.

Ответ

.

Пример 3. Найти первый, второй и третий дифференциалы

Найти дифференциалы первого, второго и третьего порядка функции
.

Решение стандартным способом

Можно сначала найти производные первого, второго и третьего порядков: и , а затем применить формулы . Но мы проделаем вычисления, применяя свойства дифференциалов.

Представим исходную функцию как сложную:
, где .
Найдем дифференциал , применяя формулу .
;
(3.1.1)   .

Первый дифференциал имеет инвариантную форму при замене переменных. Поэтому найдем дифференциал от более простой функции , и подставим и (3.1.1) для :
.
Попутно заметим, что отсюда
(3.1.2)   .
Впоследствии мы будем применять эту формулу. Итак, мы нашли первый дифференциал.
(3.1.3)   .

Найдем второй дифференциал. Согласно общим правилам, для этого мы считаем, что в (3.1.3) является постоянной, а – функция, зависящая только от одной переменной x. При этом возникающий дифференциал независимой переменной приравниваем к дифференциалу независимой переменной первого дифференциала (3.1.3).

Находим дифференциал от (3.1.3), считая функцией от x, а – постоянной.
Применяем формулу .
(3.1.4)   .
Вычисляем дифференциал произведения, и используем (3.1.2) и (3.1.4).
;
.
Выносим постоянные 3 и за знак дифференциала.

.
Тем самым мы нашли дифференциал второго порядка:
(3.1.5)   .

Тем же способом находим третий дифференциал. То есть, считаем что и, следовательно, – постоянные, а в (3.1.5) – функция, зависящая только от x.
;
;

;
;

;
.

Ответ

;
;
.
Заметим, что для степеней дифференциалов независимой переменной принято опускать скобки. Поэтому две последние формулы можно записать так.
;
.

Решение подстановкой

Теперь продемонстрируем, что такое неинвариантность формы дифференциалов второго и высших порядков. Для этого мы сделаем замену переменной
, и вычислим дифференциалы, используя только переменную t. А затем перейдем к переменной x, и получим окончательный результат.

Переходим к переменной t по формулам:
, где .
Первый дифференциал имеет инвариантную форму:
.
Чтобы его найти, нужно просто вместо переменной x использовать переменную t, и применить определение первого дифференциала.
;
(3.2.1)   .

Найдем второй дифференциал. Определение дифференциалов второго и высших порядков отличается от определения дифференциала первого порядка. Если мы вычисляем дифференциал функции, зависящей от переменной x, то мы должны найти дифференциал от первого дифференциала, в котором является постоянной. Когда мы переходим к переменной t, мы должны считать постоянной именно , а не . Поскольку
,
то уже не будет постоянной. В этом как раз и проявляется неинвариантность формы дифференциалов высших порядков.

Итак, находим второй дифференциал, используя переменную t. Для этого вычисляем дифференциал от (3.2.1) считая, что есть функция от t.

;
(3.2.2)   .

Тем же способом находим дифференциал третьего порядка. Для этого вычисляем дифференциал от (3.2.2) считая, что и являются функциями от t.


.
Вычисляем производную по переменной .
.
Окончательно имеем.
;
(3.2.3)   .

Формулы (3.2.1), (3.2.2) и (3.2.3) дают выражения дифференциалов первого, второго и третьего порядка по переменной x, выраженных через переменную t. Переходим к переменой x, считая, что является постоянной.
;
;
;
;
;
;
;
;
.
Подставляем в (3.2.1), (3.2.2) и (3.2.3).
;
;

.

Ответ

;
;
.

Пример 4. Вычислить приближенное значение с помощью дифференциала

С помощью дифференциала вычислить приближенное значение кубического корня   .

Решение

Рассмотрим функцию . Требуется найти ее значение в точке .
Воспользуемся тем, что мы можем легко найти значение при :
.
Введем приращения аргумента и функции :
;
.
Тогда ;
;
(4.1)   .
Таким образом, чтобы определить значений функции в точке , зная ее значение в , нужно найти приращение в при приращении аргумента .

Согласно определению дифференциала,
(4.2)   при .
То есть при достаточно малом значении приращения аргумента , приращение функции будет близким к дифференциалу:
(4.3)   .
Таким образом, для решения примера, нам нужно найти дифференциал функции в точке . После чего, используя (4.3), мы найдем приближенное значение приращения функции, и по формуле (4.1) – искомое значение корня.

Находим производную, а затем дифференциал функции в точке .
(4.4)   ;
;
.
Приближенное значение приращения функции:
.
По формуле (4.1) находим искомое приближенное значение корня.
.

Ответ

.

Применять в прикладных задачах подобный метод приближенных вычислений, как мы сделали в этом примере нельзя, поскольку мы не нашли погрешность, с которой получили значение корня . С помощью одной только формулы (4.2) найти погрешность не возможно. Для ее оценки требуется дополнительное исследование. Его можно выполнить, применяя теорию ряда Тейлора.

Разложим функцию в ряд Тейлора, оставляя только линейное слагаемое по , и записав остаточный член в форме Лагранжа:
(4.5)   .
Точное значение не известно. Но известно, что оно заключено в интервале
(4.6)   .
Это позволяет сделать оценку точности вычисления.

Погрешность вычисления определяется последним слагаемым в (4.5):
.
Оценим эту величину. Используя (4.4), находим .
;
. Тогда
.
возрастает с ростом . Можно найти нижнюю границу ее значения в интервале (4.6).
.
Отсюда получаем оценку погрешности вычислений:
(4.7)   .
По абсолютной величине, наибольшая погрешность составляет
.
Из (4.7) находим, что значение числа заключено в пределах
;
;
(4.8)   .
Поэтому корректный результат решения этого примера имеет вид (4.8). На практике часто пишут результат в более удобной форме:
.
Точное значение корня, округленное до 10-го знака после запятой:
.
Как и следовало ожидать, оно находится в установленном интервале (4.8).

Определения и формулы, применяемые при вычислении дифференциалов

Далее для справок изложены основные формулы, используемые в задачах на нахождение дифференциала. Подробное изложение теоретического материала приводится на странице Дифференциал функции в точке.

Первый дифференциал функции и его свойства

Дифференциал функции в точке

Пусть функция дифференцируема в некоторой точке .
Тогда ее приращение в этой точке можно представить в виде суммы линейной функции от приращения ее аргумента и бесконечно малой функции по сравнению с :
.
Дифференциалом функции в точке называется главная линейная часть приращения функции, соответствующая приращению независимой переменной :
.
То есть это приращение функции, в котором опущены слагаемые, содержащие бесконечно малые величины по сравнению с приращением аргумента .
Дифференциал обозначается как или , и является функцией двух переменных: и . Он также называется дифференциалом первого порядка или первым дифференциалом.

Дифференциал независимой переменной

– это приращение аргумента функции:
.
Он является независимой переменной.

Дифференциал функции имеет следующие обозначения:
;
;
;
.

Дифференциалы второго и высших порядков

Дифференциал n-го порядка функции в точке

Пусть функция n раз дифференцируема в точке x.
Дифференциалом n-го порядка функции в точке называется дифференциал от дифференциала - го порядка в этой точке при следующих ограничениях.
1. Считается, что дифференциал - го порядка является функцией, зависящей только от одной переменной – аргумента функции . То есть дифференциал независимой переменной рассматривается как постоянная.
2. Приращение аргумента приравнивается к приращению аргумента дифференциала -го порядка.
Дифференциал n-го порядка также называют n-м дифференциалом функции в точке. Он обозначается одним из способов:
,
и определяется по формуле:
(2.4)   .

Значение выражения зависит от контекста, в котором оно применяется.
Если оно применяется при вычислении n-го дифференциала, то
.
Если это первый дифференциал функции , то
.

Далее перечислены основные свойства дифференциалов высших порядков. Здесь – функции, зависящие от переменной ; – постоянная.
Дифференциал суммы и разности.
.
Вынесение постоянной за знак дифференциала.
.
Дифференциал произведения двух функций.

.
Как следствие, дифференциал произведения m функций.
.
Суммирование ведется по всем возможным целым значениям , сумма которых равна n, и каждое из которых заключено в пределах .

Формулу Тейлора

можно выразить через дифференциалы высших порядков
.
Здесь – приращение функции в точке .
Напомним, что согласно определению, дифференциал независимой переменной является ее приращением
.

Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.

Автор: Олег Одинцов.     Опубликовано: 12-02-2023