Дифференциал функции в точке
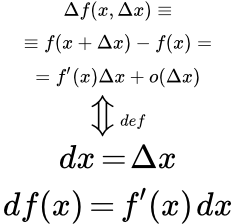
Первый дифференциал функции
Определение первого дифференциала функции
- Дифференциал функции в точке
- Пусть функция y = f (x) дифференцируема в некоторой точке x0.
Тогда ее приращение в этой точке можно представить в виде суммы линейной функции от приращения ее аргумента Δx и бесконечно малой функции по сравнению с Δx:
Δ f (x0, Δx) ≡ f (x0 + Δx) – f (x0) = f ′(x0)Δx + o(Δx).
Дифференциалом df функции f (x) в точке x0 называется главная линейная часть приращения функции, соответствующая приращению Δx независимой переменной x:
df = f ′(x0)Δx.
То есть это приращение функции, в котором опущены слагаемые, содержащие бесконечно малые величины по сравнению с приращением аргумента Δx.
Дифференциал обозначается как dy, df или df (x0), и является функцией двух переменных: x0 и Δx. Он также называется дифференциалом первого порядка или первым дифференциалом.
- Дифференциал независимой переменной
- – это приращение аргумента функции:
dx = Δx.
Он является независимой переменной.
С учетом определений, дифференциал функции y = f (x) в точке x0 имеет следующий вид.
(1.1) df (x0) = f ′(x0) dx.
Его также можно записать в одной из следующих форм.
df = f ′(x0) dx;
dy = f ′(x0) dx;
dy = dydx dx |x = x0.
Поскольку дифференциал функции зависит от двух переменных, то его следовало бы писать так: df (x0, dx). Однако, переменную dx, как правило опускают, и пишут сокращенно df (x0). При этом всегда подразумевают ее присутствие. То есть сначала мы вводим новую независимую переменную dx, являющуюся приращением аргумента функции, а затем, используя две независимые переменные x0 и dx, определяем дифференциал.
Поскольку точка x0 сама является переменной, то ее, как правило, обозначают тем же символом, что и аргумент функции. Тогда (1.1) и последующие формулы примут более простой вид.
df (x) = f ′(x) dx;
df = f ′(x) dx;
dy = f ′(x) dx;
dy = dydx dx.
В чем смысл первого дифференциала
Зачем вводят дифференциалы? Не проще ли использовать вместо них приращения независимой переменной и функции?
– Дифференциалы вводят для сокращения записей расчетов, в которых используются стремящиеся к нулю приращения. На завершающем этапе таких расчетов выполняют предельный переход, в результате которого все о - малые функции от приращений стремятся к нулю. Поэтому применяют систему записи, в которой эти о - малые исключены с самого начала.
В строгом варианте, нужно выписать точные выражения для приращений, типа
Δ f (x, Δx) = f ′(x)Δx + o(Δx).
По завершении алгебраических операций, выполнить предельный переход
при Δx → 0, o(Δx)Δx → 0.
Вместо этого с самого начала оставляют только главные части приращений, которые называются дифференциалами:
df (x, dx) ≡ df (x) = f ′(x) dx.
В результате получают выражения, линейные по дифференциалам, справедливые для приращений, когда они стремятся к нулю.
Можно сказать и так.
Дифференциалы – это приращения, в которых отброшены все функции, о - малые от приращений независимых переменных.
Первые дифференциалы – это выражения, в которых оставлены только линейные части приращений.
Также говорят, что
Дифференциалы – это бесконечно малые приращения.
Геометрический смысл дифференциала
Если существует конечная производная функции y = f (x) в точке x = x0,то дифференциал dy функции в точке x0 – это приращение ординаты касательной, проведенной к графику функции в точке x0, соответствующее приращению аргумента Δx.
Дифференциал dx независимой переменной x – это приращение аргумента функции: dx = Δx.
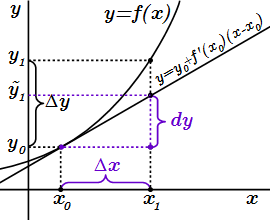
На странице «Геометрический смысл производной» мы выяснили, что уравнение касательной к графику функции y = f (x) имеет вид:
(1.2) y = y0 + f ′(x0)(x – x0),
где y0 = f (x0).
В точке с абсциссой x = x0, ордината касательной равна y0. Рассмотрим точку x1 = x0 + Δx, в которой приращение абсциссы равно Δx = x1 – x0. Из уравнения (1.2) находим ординату касательной в этой точке:
~y1 = y0 + f ′(x0)(x0 + Δx – x0) = y0 + f ′(x0)Δx.
Приращение ординаты касательной
~y1 – y0 = f ′(x0)Δx.
Как видно, оно совпадает с дифференциалом функции в точке x0
dy = f ′(x0)Δx.
Свойства первого дифференциала
Арифметические свойства дифференциалов
Тогда в этой точке
(1.3) d ( f (x) ± g(x)) = df (x) ± dg(x) (дифференциал суммы функций);
(1.4) d ( f (x) ⋅ g(x)) = g(x) ⋅ df (x) + f (x) ⋅ dg(x) (дифференциал произведения);
(1.5) d( f (x)g(x) ) = g(x) df (x) – f (x) dg(x)g 2 (x), при g(x) ≠ 0 (дифференциал частного).
Постоянный множитель можно выносить из-под знака дифференциала:
(1.6) d (Cf (x)) = C df (x).
Доказательство следует из определения дифференциала (1.1) и формул производных суммы, произведения и частного.
d ( f (x) ± g(x)) = ( f (x) ± g(x)) ′dx = ( f ′(x) ± g ′(x))dx =
f ′(x)dx ± g ′(x)dx = df (x) ± dg(x);
d ( f (x) ⋅ g(x)) = ( f (x) ⋅ g(x)) ′dx = ( f ′(x) ⋅ g(x) + f (x) ⋅ g ′(x))dx =
g(x) ⋅ f ′(x)dx + f (x) ⋅ g ′(x)dx = g(x) ⋅ df (x) + f (x) ⋅ dg(x);
d( f (x)g(x) ) = ( f (x)g(x) ) ′dx = f ′(x)g(x) – f (x)g ′(x)g 2 (x) dx =
g(x) f ′(x)dx – f (x)g ′(x)dxg 2 (x) = g(x) df (x) – f (x) dg(x)g 2 (x);
d (Cf (x)) = (Cf (x)) ′dx = Cf ′(x)dx = C df (x).
Инвариантность формы первого дифференциала
При этом функция t(x) имеет производную в точке x, а функция g имеет производную в точке t = t(x).
Тогда дифференциал первого порядка функции, выраженный через переменную x имеет ту же форму, что и дифференциал, выраженный через переменную t:
dy = dydx dx = dydt dt.
Эту же формулу можно записать так:
dy = f ′x (x) dx = g ′t (t) dt.
По теореме о производной сложной функции, в точке x существует производная y по x. Применим эту теорему и подставим dt = t ′x (x) dx.
dy = f ′x (x) dx = g ′t (t) ⋅ t ′x (x) dx = g ′t (t) dt.
Здесь мы выполнили доказательство, использую характеристики функций f , g, t. Проделаем тоже самое, использую переменные y, t, x.
dy = dydx dx = dydt ⋅ dtdx dx = dydt dt.
Можно проделать вывод и просто сделав подстановку t = t(x).
dy = dydt dt = dydt ⋅ dtdx dx = dydx dx.
В известном смысле с первыми производными можно обращаться как с дробями, составленными из дифференциалов.
Примечание.
В формуле dy = g ′t(t) dt, dt является дифференциалом независимой переменной, то есть приращением переменной t.
В формуле dt = t ′x (x) dx, dt уже дифференциал зависимой переменной. Он может отличаться от приращения Δt на о - малое по сравнению с dx при dx → 0.
Δt = t ′x (x) dx + o(dx);
Δt = dt + o(dx).
Дифференциалы второго и высших порядков
Проблемы определения
Попробуем найти дифференциал второго порядка от функции y = f (x).
При определении дифференциала dy первого порядка, мы вводим новую независимую переменную dx, которую называем приращением или дифференциалом независимой переменной. После этого dy определяется по формуле.
(2.1) dy = f ′(x) dx.
Первый дифференциал dy является функцией двух переменных: x и dx.
Тогда, чтобы найти второй дифференциал, мы должны найти дифференциал от функции двух переменных (2.1). Для этого нужно ввести приращения δx и δdx переменных x и dx. Используя арифметические свойства (1.4), находим дифференциал от (2.1).
δdy = (δf ′(x)) dx + f ′(x) δdx = f ′′(x) ⋅ δx ⋅ dx + f ′(x) δdx;
(2.2) δdy = f ′′(x) ⋅ δx ⋅ dx + f ′(x) ⋅ δdx.
Как видно, он является функцией уже четырех переменных: x, dx, δx, δdx.
Действуя подобным способом, мы найдем, что дифференциал третьего порядка будет зависеть от восьми переменных, а дифференциал произвольного, n - го порядка – от 2 n. Применять такие дифференциалы будет затруднительно. И, при этом, не вполне очевиден смысл дополнительных переменных.
Давайте упростим задачу. Рассмотрим дифференциал первого порядка как функцию только одной переменной x. То есть считаем, что дифференциал независимой переменной dx является постоянной. Тогда δdx = 0, и вместо (2.2) получим:
(2.3) δdy = f ′′(x) ⋅ δx ⋅ dx.
Теперь второй дифференциал уже является функцией трех переменных x, dx, δx. Тогда при каждом взятии дифференциала от дифференциала, будет появляться новая переменная – новое приращение переменной x. Дифференциал n - го порядка будет функцией, зависящей от n + 1 переменных.
Сделаем еще проще. Приравняем приращения независимых переменных. То есть при определении второго дифференциала, приравняем новую переменную δx к dx.
δdy = f ′′(x) ⋅ δx ⋅ dx = f ′′(x) ⋅ dx ⋅ dx = f ′′(x)(dx) 2.
Теперь, как и первый дифференциал, второй дифференциал является функцией, зависящей от двух переменных – x и dx.
Такое определение является общепринятым. Поскольку δx = dx, то и в дифференциале функции вместо символа δ используют символ d:
d(dy) ≡ d 2 y.
Важно отметить, что при записи произведения приращений независимой переменной опускают скобки:
dx ⋅ dx ≡ (dx) 2 ≡ dx 2.
Тогда второй дифференциал функции y = f (x) может иметь следующие формы записи:
d 2 y ≡ d 2 f ≡ d 2 f (x) = f ′′(x)(dx) 2 ≡ f ′′(x) dx 2.
Аналогично, для дифференциала n - го порядка, имеем
d n y ≡ d n f ≡ d n f (x) = f (n) (x)(dx) n ≡ f (n) (x) dx n.
Значение выражения dx n зависит от контекста, в котором оно применяется.
Если оно применяется при вычислении n - го дифференциала, то
dx n ≡ (dx) n.
Если это первый дифференциал функции f (x) = x n, то
dx n ≡ d(x n) = (x n) ′dx = nx n – 1 dx.
Определение
- Дифференциал n-го порядка функции в точке
- Пусть функция y = f (x) n раз дифференцируема в точке x.
Дифференциалом n-го порядка d n f функции в точке x называется дифференциал от дифференциала n – 1 - го порядка в этой точке при следующих ограничениях.
1. Считается, что дифференциал n – 1 - го порядка является функцией, зависящей только от одной переменной – аргумента функции x. То есть дифференциал независимой переменной dx рассматривается как постоянная.
2. Приращение аргумента δx приравнивается к приращению аргумента dx дифференциала n – 1-го порядка.
Дифференциал n-го порядка также называют n-м дифференциалом функции в точке. Он обозначается одним из способов:
d n y ≡ d n f ≡ d n f (x),
и определяется по формуле:
(2.4) d n y = f (n) (x)(dx) n ≡ f (n) (x)dx n.
Формулу (2.4) легко получить по индукции. Для n = 1 она является первым дифференциалом:
dy = f ′(x) dx.
Для n > 1 имеем.
d n f = d(d n – 1 f ) = d ( f (n – 1) (x)(dx) n – 1)|dx = const = f n (x) ⋅ δx ⋅ (dx) n – 1 | δx = dx =
f (n) (x)(dx) n ≡ f (n) (x)dx n.
Свойства
Поскольку дифференциал n-го порядка функции y = f (x) равен n-й производной, умноженной на (dx) n:
d n y = f (n) (x) (dx) n,
то часть его свойств следует из свойств производных высших порядков. При этом (dx) n рассматривается как постоянная, не зависящая от x величина.
Арифметические свойства дифференциалов высших порядков
Здесь f , f 1, f 2, . . . f m – дифференцируемые функции в точке x; C – постоянная.Дифференциал суммы и разности.
d n ( f 1 ± f 2) = d n f 1 + d n f 2.
Вынесение постоянной за знак дифференциала.
d n (Cf ) = Cd n f .
Дифференциал произведения двух функций.
d n ( f 1 ⋅ f 2) = d n f 1 ⋅ f 2 + nd n – 1 f 1 ⋅ df 2 + n(n – 1)2! d n – 2 f 1 ⋅ d 2 f 2 + ⋅ ⋅ ⋅ +
n!(n – k)!k! d n – k f 1 ⋅ d k f 2 + ⋅ ⋅ ⋅ + f 1 ⋅ d n f 2.
Дифференциал произведения m функций.
d n ( f 1 ⋅ f 2 ⋅ ⋅ ⋅ f m) = ΣΣ ki = n n!k1 !k2 !⋅ ⋅ ⋅km ! d k1 f 1 ⋅ d k2 f 2 ⋅ ⋅ ⋅d km f m.
Суммирование ведется по всем возможным целым значениям k1, k2, . . .km, сумма которых равна n, и каждое из которых заключено в пределах 0 ≤ ki ≤ n.
Связь дифференциалов с формулой Тейлора
Первый дифференциал df функции y = f (x) содержит только слагаемые, линейные по приращению dx аргумента x. Дифференциал второго порядка d 2 f – слагаемые, квадратичные по dx. Дифференциал n - го порядка d n f – слагаемые со степенью (dx) n.
В связи с этим, формулу Тейлора
Δ f = f ′(x)Δx + 12! f ′′(x)(Δx) 2 + 13! f ′′′(x)(Δx) 3 + ⋅ ⋅ ⋅ + 1n! f (n) (x)(Δx) n + ⋅ ⋅ ⋅
можно выразить через дифференциалы высших порядков
Δ f = df + 12! d 2 f + 13! d 3 f + ⋅ ⋅ ⋅ + 1n! d n f + ⋅ ⋅ ⋅.
Здесь Δ f = f (x + Δx) – f (x) – приращение функции в точке x.
Напомним, что согласно определению, дифференциал независимой переменной является ее приращением
dx = Δx.
Не инвариантность формы дифференциала второго и высших порядков
Дифференциалы второго порядка
Выше мы установили, что форма первого дифференциала инвариантна, то есть не меняется при замене переменных. Так, если мы от переменной x перейдем к переменной t, сделав подстановку t = t(x), то первый дифференциал будет иметь один и тот же вид, отличающийся лишь заменой x на t:
dy = dydx dx = dydt dt.
Однако для дифференциалов второго и высших порядков, такая инвариантность отсутствует – при замене переменной его форма может иметь другой вид. В общем случае
d 2 y = d 2 ydx 2 (dx) 2 ≠ d 2 ydt 2 (dt) 2.
См. Пример вычисления дифференциалов высших порядков с помощью замены переменной
Покажем это. Рассмотрим функцию y = f (x). Согласно определению, ее второй дифференциал
d 2 y = f ′′xx (x) (dx) 2.
Перейдем к переменной t = t(x), рассматривая f как сложную функцию
f (x) = g(t(x)).
Дифференцируем по переменной x, применяя правила дифференцирования сложной функции и произведения:
f ′′xx(x) = ( f ′x(x)) ′x = (g ′t (t(x)) ⋅ t ′x(x)) ′x = (g ′t (t(x))) ′x ⋅ t ′x(x) + g ′t(t(x)) ⋅ t ′′xx(x) =
g ′′tt (t(x)) ⋅ t ′x(x) ⋅ t ′x(x) + g ′t(t(x)) ⋅ t ′′xx(x);
f ′′xx(x) = g ′′tt (t(x)) ⋅ t ′x(x) ⋅ t ′x(x) + g ′t(t(x)) ⋅ t ′′xx(x).
Здесь мы нижним индексом обозначили переменную, по которой выполняется дифференцирование. Делается это только для удобства восприятия материала. В этом нет необходимости, поскольку, например, производная f ′ без нижнего индекса обозначает производную по ее аргументу, то есть по x. Аналогично и для других функций g(t) и t(x). Можно было опустить все нижние индексы без возникновения двусмысленности в изложении.
Подставляем в дифференциал второго порядка, и учитываем, что dt = t ′x(x) dx; d 2 t = t ′′xx(x)(dx) 2.
d 2 y = f ′′xx(x) dx 2 ≡ f ′′xx(x) (dx) 2 =
g ′′tt(t(x)) ⋅ t ′x(x) dx ⋅ t ′x(x) dx + g ′t(t(x)) ⋅ t ′′xx(x) (dx) 2 = g ′′tt(t)(dt) 2 + g ′t(t) d 2 t.
В результате мы получили формулу, связывающую дифференциал второго порядка, выраженный через переменную t:
d 2 y = g ′′tt (t) (dt) 2 + g ′t (t) d 2 t.
Отсюда видно, что в дифференциале, выраженном через переменную t появляется дополнительное слагаемое g ′t (t) d 2 t, которое отсутствует в дифференциале, выраженном через переменную x. То есть форма второго дифференциала не инвариантна при замене переменной.
Выше мы выполнили выкладки, используя характеристики функций. Проделаем тоже самое, используя вместо характеристик переменные.
y ′′xx = (y ′x ) ′x = (y ′t ⋅ t ′x ) ′x = (y ′t) ′x ⋅ t ′x + y ′t ⋅ t ′′xx = y ′′tt ⋅ t ′x ⋅ t ′x + y ′t ⋅ t ′′xx;
y ′′xx = y ′′tt ⋅ t ′x ⋅ t ′x + y ′t ⋅ t ′′xx.
Подставляем в дифференциал второго порядка.
d 2 y = y ′′xx (dx) 2 = y ′′tt ⋅ t ′x dx ⋅ t ′x dx + y ′t ⋅ t ′′xx (dx) 2 = y ′′tt(dt) 2 + y ′t d 2 t.
Проделаем тоже самое, используя переменные и обозначения производных в форме отношений дифференциалов.
d 2 ydx 2 = ddx ( dydx ) = ddx ( dydt ⋅ dtdx ) = ( ddx dydt ) ⋅ dtdx + dydt ⋅ ( ddx dtdx ) =
dtdx ⋅ ( ddt dydt ) ⋅ dtdx + dydt ⋅ d 2 t(dx) 2 = d 2 y(dt) 2 ⋅ ( dtdx ) 2 + dydt ⋅ d 2 t(dx) 2;
d 2 y(dx) 2 = d 2 y(dt) 2 ⋅ ( dtdx ) 2 + dydt ⋅ d 2 t(dx) 2;
d 2 y = d 2 y(dx) 2 (dx) 2 = d 2 y(dt) 2 ⋅ ( dtdx ) 2 (dx) 2 + dydt ⋅ d 2 t(dx) 2 (dx) 2 =
d 2 y(dt) 2 ⋅ (dt) 2 + dydt ⋅ d 2 t;
d 2 y = d 2 y(dt) 2 ⋅ (dt) 2 + dydt ⋅ d 2 t.
Итак, форма дифференциала второго порядка, выраженного через переменную x отличается от формы дифференциала, выраженного через переменную t:
d 2 y = d 2 y(dx) 2 ⋅ (dx) 2 = d 2 y(dt) 2 ⋅ (dt) 2 + dydt ⋅ d 2 t.
Теорема о не инвариантности формы дифференциала высшего порядка
Пусть функцию y = f (x) можно представить как сложную: y = g(t(x)).При этом функции f , t и g дифференцируемы n раз в точках x, x и t = t(x), соответственно.
И пусть n > 1.
Тогда форма дифференциала n - го порядка функции, выраженной через переменную x, при n > 1, не совпадает с формой дифференциала этого же порядка, выраженного через переменную t:
d n y = d n ydx n (dx) n ≠ d n ydt n (dt) n.
Дифференциал n-го порядка в точке x имеет вид
(2.5) d n y = d n ydx n (dx) n.
Перепишем n-ю производную следующим образом:
d n ydx n = ( ddx ) n y = ddx ⋅ ⋅ ⋅ ddx ⋅ ddxn раз y.
В последнем множителе применим правило дифференцирования сложной функции:
d n ydx n = ( ddx ) n – 1 ⋅ dydx = ( ddx ) n – 1 ⋅ ( dtdx ⋅ dydt ).
Применим правило дифференцирования произведения и сложной функции:
ddx ( dtdx ⋅ dydt ) = d 2 tdx 2 ⋅ dydt + ( dtdx ⋅ ddx dydt ) =
d 2 tdx 2 ⋅ dydt + ( dtdx ⋅ dtdx ⋅ ddt dydt ) = d 2 tdx 2 ⋅ dydt + ( dtdx ) 2 ⋅ d 2 ydt 2;
d n ydx n = ( ddx ) n – 2 ddx ( dtdx ⋅ dydt ) = ( ddx ) n – 2 [ d 2 tdx 2 ⋅ dydt + ( dtdx ) 2 ⋅ d 2 ydt 2 ].
Применяя эту процедуру n – 2 раза найдем, что в состав d n ydx n входит слагаемое, содержащее n-ю производную t по x:
d n ydx n = dydt ⋅ d n tdx n + ⋅ ⋅ ⋅.
Выделим его в n-ом дифференциале (2.5):
d n y = d n ydx n (dx) n = dydt ⋅ d n tdx n (dx) n + ⋅ ⋅ ⋅ = dydt ⋅ d n t + ⋅ ⋅ ⋅.
Таким образом мы показали, что n-й дифференциал, выраженный через переменную t имеет в своем составе слагаемое dydt ⋅ d n t, которого нет в дифференциале (2.5), выраженного через переменную x. То есть форма дифференциала n - го порядка функции, выраженной через переменную x не совпадает с формой дифференциала этого же порядка, выраженного через переменную t.
Инвариантная форма дифференциала второго порядка
Дифференциалы второго и высших порядков определены с двумя ограничениями. Поэтому они утратили свойство инвариантности формы при замене переменной. Покажем, что если убрать первое ограничение и оставить второе, то дифференциал второго порядка сохранит свойство инвариантности.
Рассмотрим дифференциал второго порядка общего вида (2.2):
δdy = f ′′(x) ⋅ δx ⋅ dx + f ′(x) ⋅ δdx.
Приравняем приращения: δx = dx,
(2.6) d 2 y = f ′′(x) ⋅ (dx) 2 + f ′(x) d 2 x.
Здесь x, dx, d 2 x – независимые переменные.
Проведем вывод, используя обозначения переменных. Тогда (2.6) примет вид
(2.7) d 2 y = y ′′xx ⋅ (dx) 2 + y ′x d 2 x.
Перейдем к новым независимым переменным t, dt d 2 t, выполняя преобразование t = t(x).
y ′x = t ′xy ′t;
y ′′xx = (t ′xy ′t) ′x = (t ′x) ′xy ′t + t ′x(y ′t) ′x = t ′′xxy ′t + t ′xt ′x(y ′t) ′t = t ′′xxy ′t + t ′xt ′xy ′′tt;
y ′′xx = t ′′xxy ′t + t ′xt ′xy ′′tt.
Подставляем в (2.7) и выполняем преобразования.
d 2 y = (t ′′xxy ′t + t ′xt ′xy ′′tt)(dx) 2 + y ′x d 2 x;
d 2 y = t ′xt ′xy ′′tt(dx) 2 + t ′′xxy ′t(dx) 2 + y ′x d 2 x;
d 2 y = y ′′tt(t ′xdx) 2 + t ′′xxy ′t(dx) 2 + t ′xy ′t d 2 x;
d 2 y = y ′′tt(dt) 2 + y ′t(t ′′xx(dx) 2 + t ′x d 2 x);
d 2 y = y ′′tt(dt) 2 + y ′td 2 t.
Видно, что дифференциал d 2 y имеет форму (2.7), в которой переменная x заменена переменной t.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Г.Н. Яковлев. Лекции по математическому анализу. Часть 1. Москва, 2001.
Автор: Олег Одинцов. Опубликовано: Изменено: