Физический смысл производной

На примере из механики показывается, что мгновенная скорость движения точки равна производной координаты этой точки по времени. Ускорение равно производной скорости по времени, или второй производной ее координаты по времени. Аналогичным образом, мгновенная скорость изменения любой физической величины равна производной этой величины по времени.

Физический смысл производной заключается в том, что мгновенная скорость изменения любой физической величины равна производной этой величины по времени.

Так, в механике, наиболее распространенными физическими величинами являются координаты точки x, y, z. При прямолинейном движении, мгновенная скорость движения точки равна производной ее координаты по времени. При движении в пространстве, проекции мгновенной скорости на оси координат равны производным координат по времени: v_x = dxdt,  v_y = dydt,  v_z = dzdt.

Прямолинейное движение

По мере развития механики, стал проясняться следующий факт. Если тела не взаимодействуют друг с другом, то они движутся прямолинейно и равномерно. Но если между ними происходит взаимодействие, то они движутся с переменной скоростью. Поэтому встал вопрос об определении мгновенного значения скорости при неравномерном движении.

Для начала рассмотрим прямолинейное движение. Пренебрежем размерами тела и будем рассматривать его как материальную точку, которую обозначим буквой M. Направим ось OX системы координат вдоль линии движения точки M. Пусть нам известна зависимость координаты x от времени t: x = x(t). Нашей задачей является определение мгновенной скорости точки M в произвольный момент времени.

Равномерное движение

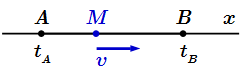
Если точка движется равномерно, то ее скорость постоянна. Для ее определения, нужно разделить перемещение ΔS на отрезок времени Δt, в течении которого произошло это перемещение. Пусть в момент времени t_A, точка M находилась в точке A с координатой x_A, а в момент времени t_B – в точке B с координатой x_B. Тогда перемещение точки M составило ΔS = x_B – x_A. Промежуток времени, в течении которого произошло это перемещение: Δt = t_B – t_A. Скорость движения:
(1)   v = ΔSΔt = x_B – x_At_B – t_A.
При равномерном движении скорость постоянна: v = const. Поэтому результат вычисления не зависит от того, какие точки A и B мы выбираем. Например, если бы мы вместо точки B взяли другую точку C, то получили бы, то же самое значение скорости:
v = x_B – x_At_B – t_A = x_C – x_At_C – t_A.

Неравномерное движение

При неравномерном движении скорость не является постоянной. Поэтому, если проделать вычисления по формуле (1), то мы получим только среднее значение скорости на отрезке AB:
(2)   v_AB = x_B – x_At_B – t_A.

Однако мы можем предположить, что если приближать точку B к A, то среднее значение v_AB не будет хаотично колебаться, а будет стремиться к некоторой величине, которую можно принять за мгновенную скорость движения точки M при t = t_A.

Если использовать только алгебру, то можно дать только определение средней скорости движения тела на некотором отрезке AB. Чтобы дать четкое математическое определение мгновенной скорости, потребовалось создать новый раздел математики – математический анализ, или анализ бесконечно малых величин. Основой математического анализа является теория пределов. В настоящее время эта теория хорошо разработана, и мы можем использовать уже готовый математический аппарат. Тогда разумно определить мгновенную скорость в точке A как предел, к которому стремится средняя скорость тела M на отрезке AB, при стремлении B к A.

Мгновенная скорость точки

Пусть точка M движется вдоль оси координат Ox. И пусть движение описывается законом x = x(t). Мгновенной скоростью точки M в момент времени t = t_A называется предел, к которому стремится средняя скорость движения на отрезке t ∈ [t_A,  t_B] при t_B → t_A:
v(t_A) = lim_{tB → tA} x_B – x_At_B – t_A = lim_{tB → tA} x(t_B) – x(t_A)t_B – t_A = x^′(t_A).
То есть мгновенная скорость движения точки в момент времени t_A равна производной ее координаты по времени, взятой в момент времени t = t_A:
v(t_A) = x^′(t_A).

Заметим, что в механике и физике производная по времени обозначается не штрихом, а точкой над символом переменной. Тогда в физике, предыдущая формула имеет следующий вид:
v(t_A) =^.x(t_A).

Движение в пространстве

Теперь рассмотрим движение точки M в трехмерном пространстве. В этом случае, ее положение определяется тремя координатами (x, y, z) – проекциями точки на оси координат. Тогда мы можем применить результаты, полученные для одномерного движения, к трехмерному. Пусть в момент времени t_A, точка M находилась в точке A с координатами (x_A, y_A, z_A), а в момент времени t_B – в точке B с координатами (x_B, y_B, z_B). Проекция средней скорости точки на ось Ox равна
v_ABx = x_B – x_At_B – t_A.
При стремлении B к A, мы получаем проекцию мгновенной скорости на ось Ox:
v_x (t_A) = lim_{tB → tA} x_B – x_At_B – t_A = lim_{tB → tA} x(t_B) – x(t_A)t_B – t_A = x^′(t_A);
v_x (t_A) = x^′(t_A).

Аналогичным образом, рассматривая изменения других координат, мы найдем проекции мгновенной скорости точки M на оси Oy и Oz:
v_y (t_A) = y^′(t_A);  v_z (t_A) = z^′(t_A).
Таким образом, при движении в пространстве, проекции мгновенной скорости движения точки M на оси координат в момент времени t = t_A равны производным ее координат по времени, взятых в момент времени t = t_A:
(3)   v_x (t_A) = x^′(t_A);   v_y (t_A) = y^′(t_A);  v_z (t_A) = z^′(t_A).
Если ввести радиус-вектор ^→r точки M с координатами (x, y, z), и заменить обозначение момента времени t_A → t, то формулы (3) можно записать в векторном виде:
^→v(t) =^→r^′(t).
где ^→v(t) = (v_x (t),  v_y (t),  v_z (t)) – вектор мгновенной скорости точки M в момент времени t; ^→r^′(t) = (x^′(t),  y^′(t),  z^′(t)) – производная радиус-вектора точки M по времени.

Таким образом, при движении в пространстве, вектор мгновенной скорости движения точки M в момент времени t равен производной по времени ее радиус-вектора ^→r в этот момент времени:
(4)   ^→v(t) =^→r^′(t);
(5)   v_x (t) = x^′(t);   v_y (t) = y^′(t);  v_z (t) = z^′(t).

Ускорение

Еще одной важной физической величиной в механике, является ускорение. Оно определяется как скорость изменения скорости. Совершенно аналогичным способом получаем, что проекции ускорения ^→a на оси координат равны производным проекций скорости на эти оси:
(6)   a_x (t) = v^′_x (t);   a_y (t) = v^′_y (t);  a_z (t) = v^′_z (t).
Подставляя (5) получаем, что проекции ускорения равны вторым производным координат по времени:
a_x (t) = x^′′(t);   a_y (t) = y^′′(t);  a_z (t) = z^′′(t).
Эти уравнения можно записать в векторном виде:
^→a(t) =^→v^′(t) =^→r^′′(t);
a_x (t) = v^′_x (t) = x^′′(t);   a_y (t) = v^′_y (t) = y^′′(t);   a_z (t) = v^′_z (t) = z^′′(t).

Автор: Олег Одинцов.     Опубликовано: 02-01-2021