Пример комплексной подстановки при решении линейного неоднородного дифференциального уравнения
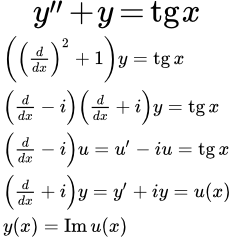
Метод понижения порядка линейного неоднородного дифференциального уравнения с комплексными корнями характеристического уравнения
Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка:
(1) .
Мы полагаем, что коэффициенты этого уравнения являются действительными числами. Здесь мы рассматриваем случай, когда характеристическое уравнение
(2)
имеет комплексные корни.
Для решения уравнения (1), применим метод понижения порядка. Поскольку коэффициенты характеристического уравнения (2) являются действительными числами, то его комплексные корни являются попарно комплексно сопряженными. Пусть – два комплексно сопряженные корня: . Запишем исходное уравнение (1) в следующем виде:
(3) ,
где – оператор дифференцирования.
Обозначим:
.
Тогда уравнение (3) принимает следующий вид:
.
Сделаем подстановку:
(4) .
Получаем уравнение первого порядка с комплексным коэффициентом :
.
Или
(5) .
Решение этого уравнения имеет следующий вид (см. страницу метод понижения порядка ):
,
где – комплексная постоянная.
Далее замечаем, что поскольку исходное уравнение (1) имеет действительные коэффициенты, то переменная u и ее производная u′ должны быть действительными. Выразим комплексный корень через действительную и мнимую части:
.
Подставим в (4):
.
Извлекая мнимую часть, получаем:
.
Отсюда
.
Таким образом, в случае с комплексными корнями, один этап решения приводит к понижению порядка на две единицы.
Пример решения дифференциального уравнения
Решить уравнение
(П1) .
Решение
Перепишем уравнение в следующем виде:
.
Вводим обозначение :
.
Характеристическое уравнение
имеет комплексные корни: . Тогда
.
Переписываем исходное уравнение:
;
.
Делаем подстановку:
;
(П2) .
Тогда уравнение принимает вид:
;
(П3) .
Это линейное неоднородное дифференциальное уравнение первого порядка. Ищем решение с помощью интегрирующего множителя. Умножим на и выполняем преобразования:
;
;
(П4) ,
где – комплексная постоянная; – действительные постоянные.
Применим тригонометрические формулы:
.
Тогда:
.
Вычисляем интеграл в (П4) с помощью подстановки .
.
Выразим арктангенс через логарифм, используя уравнение: .
;
.
Отсюда
(П5) .
С помощью (П5) имеем:
.
Тогда
.
Подставим в (П4) ⇑:
.
Отсюда
.
Согласно (П2), . Тогда
(П6) .
Теперь в правой части (П6) нам нужно отделить вещественную и мнимую части. Мнимая часть уравнения (П6) и даст искомое решение y.
Для преобразования логарифма, используем формулу: . Далее замечаем, что . Тогда при имеем:
.
При :
.
Оба случая можно записать одной формулой:
,
где при нужно взять верхний знак ′+′; при – нижний знак ′–′.
Подставим в (П6) и выполним преобразования:
;
.
Переобозначим постоянную :
(П7) .
Теперь преобразуем экспоненту с помощью формулы Эйлера: , и выразим комплексную постоянную через действительную и мнимую части: . Подставляем в (П7):
.
Выполняем преобразования:
.
Тогда
.
Отделяем мнимую часть:
.
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
