Основные понятия и определения дифференциальных уравнений
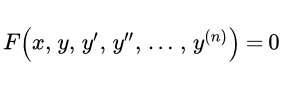
Определение дифференциальных уравнений (ДУ)
- Дифференциальное уравнение (ДУ)
- – это уравнение
,
где – независимые переменные, y – функция и – частные производные.
- Обыкновенное дифференциальное уравнение
- – это дифференциальное уравнение, которое имеет только одну независимую переменную, .
- Дифференциальное уравнение в частных производных
- – это дифференциальное уравнение, которое имеет две и более независимых переменных.
Слова “обыкновенные“ и "в частных производных" могут опускаться, если ясно, какое уравнение рассматривается. В дальнейшем рассматриваются обыкновенные дифференциальные уравнения.
- Порядок дифференциального уравнения
- – это порядок старшей производной.
Вот пример уравнения первого порядка:
Вот пример уравнения четвертого порядка:
Иногда дифференциальное уравнение первого порядка записывается через дифференциалы:
В этом случае переменные x и y являются равноправными. То есть независимой переменной может быть как x так и y. В первом случае y является функцией от x. Во втором случае x является функцией от y. Если необходимо, мы можем привести это уравнение к виду, в котором явно входит производная y′.
Разделив это уравнение на dx, мы получим:
.
Поскольку и , то отсюда следует, что
.
Решение дифференциальных уравнений
Производные от элементарных функций выражаются через элементарные функции. Интегралы от элементарных функций часто не выражаются через элементарные функции. С дифференциальными уравнениями дело обстоит еще хуже. В результате решения можно получить следующее.
- Явную зависимость функции от переменной.
- Решение дифференциального уравнения
- – это функция y = u(x), которая определена, n раз дифференцируема, и удовлетворяет исходному уравнению: .
- Неявную зависимость в виде уравнения типа Φ(x, y) = 0 или системы уравнений.
- Интеграл дифференциального уравнения
- – это решение дифференциального уравнения, которое имеет неявный вид.
- Зависимость, выраженную через элементарные функции и интегралы от них.
- Решение дифференциального уравнения в квадратурах
- – это решение ДУ, выраженное в виде комбинации элементарных функций и интегралов от них.
- Решение может не выражается через элементарные функции.
- Интегрирование дифференциального уравнения
- Процесс решения ДУ называется интегрированием дифференциального уравнения.
Поскольку решение дифференциальных уравнений сводится к вычислению интегралов, то в состав решения входит набор постоянных . Количество постоянных равно порядку уравнения.
- Общее решение дифференциального уравнения
- – это множество всех, без исключений, решений дифференциального уравнения. Общее решение ДУ n - го порядка часто записывают в виде функции, зависящей от независимой переменной x, и от n произвольных постоянных :
(1) .
- Частное решение дифференциального уравнения
- – это одно из решений ДУ. Если общее решение имеет вид (1), то в частном решении постоянные имеют заданные значения.
- Общий интеграл дифференциального уравнения
- – это общее решение, которое имеет неявный вид .
- Частный интеграл дифференциального уравнения
- – это общий интеграл при заданных значениях постоянных .
Также, под интегралом дифференциального уравнения понимают связь между переменными и производными, которая принимает постоянное значение:
.
Дифференциальное уравнение первого порядка имеет один интеграл. Уравнение n - го порядка имеет n интегралов:
;
;
. . . . . .
;
.
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
