Дифференцируемые функции в точке – определение и свойства
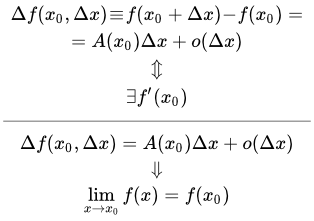
Определение дифференцируемой функции
- Дифференцируемая функция в точке
- Пусть функция f(x) определена в некоторой окрестности точки .
Функция называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде суммы линейной функции от и о-малого по сравнению с :
(1) .
Здесь – действительная величина, зависящая от , но не от ; ;
– о-малое по сравнению с при . То есть
, где .
Как мы увидим ниже, определение дифференцируемой функции одной переменной эквивалентно существованию ее производной. Тогда возникает вопрос – почему нельзя сразу дать определение, что дифференцируемая функция – это функция, имеющая производную?
Ответ на этот вопрос раскрывается при рассмотрении функций нескольких переменных. Дело в том, что производные вычисляются только от функций, зависящих от одной переменной. Для функций двух и более переменных, вначале выбирают направление приближения к заданной точке (например, ось x или ось y), а затем по этому направлению вычисляют производную. Поэтому в любой точке мы можем составить бесконечное множество производных по различным направлением. Кроме этого, по одним направлениям производные могут существовать, а по другим – нет.
Но мы хотим ввести новый класс функций, с которыми проще работать методами бесконечно малых величин. Самыми простыми являются линейные функции. Поэтому желательно выделить такой класс функций, приращения которых можно свести к линейным операциям. Это можно сделать, если потребовать, чтобы приращение функции было линейной функцией от приращений ее аргументов плюс о-малое по сравнению с этими приращениями. Такие функции называются дифференцируемыми. Например, для функции двух переменных можно записать так:
,
где – действительные величины, не зависящие от ;
– норма вектора .
- Дифференцируемая функция многих переменных в точке
- Пусть функция многих переменных определена в некоторой окрестности точки .
Функция f называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде суммы линейной функции от приращений ее аргументов и о-малого по сравнению с нормой приращений аргументов:
.
Здесь – действительные величины, зависящие от , но не от ; ;
– о-малое по сравнению с при ;
.
Свойства дифференцируемой функции
в этой точке существует производная . При этом
.
Доказательство
Таким образом, в случае функции одной переменной, дифференцируемость функции в точке эквивалентна существованию производной в этой точке. Забегая вперед укажем, что в случае функций многих переменных, для того чтобы функция была дифференцируемой в точке, необходимо, чтобы она имела в этой точке частные производные, и достаточно, чтобы она имела в этой точке непрерывные частные производные.
Тогда она непрерывна в этой точке.
Доказательство
Заметим, что обратное неверно. Если функция непрерывна в точке, то она может не быть дифференцируемой в этой точке. Так функция непрерывна для всех x, но не имеет производной при . См пример
она имеет в этой точке производные справа и слева, и они равны:
.
При этом
.
Доказательство
Доказательства теорем
Теорема о существовании производной дифференцируемой функции
Все свойства Функция дифференцируема в точке тогда и только тогда, когдав этой точке существует производная . При этом
.
1) Пусть функция дифференцируема в точке , то есть выполняется (1):
.
Разделим на и выполним переход :
;
.
Здесь, согласно свойству о-малого, . Отсюда получаем, что существует конечный предел
,
который является производной функции в точке : .
2) Пусть в точке существует производная . Это означает, что существует предел:
.
Воспользуемся свойством бесконечно малых функций. согласно которому, для существования предела необходимо и достаточно, чтобы функция имела вид: , где – бесконечно малая функция при .
В нашем случае это означает, что
.
Отсюда
.
Теорема доказана.
Теорема о непрерывности дифференцируемой функции
Все свойства Пусть функция дифференцируема в точке .Тогда она непрерывна в этой точке.
Используем определение непрерывности функции в точке. Согласно этому определению, функция f непрерывна в , если
1) определена в некоторой окрестности ;
2) существует предел при , и он равен :
.
Пусть функция дифференцируема в точке . Тогда согласно определению ⇑, она определена в некоторой окрестности точки . Пункт 1) выполнен.
Докажем, что выполняется пункт 2) . Поскольку дифференцируема в точке , то выполняется (1):
.
Выполняем предельный переход :
;
;
;
.
Сделаем подстановку . Тогда при . Последнее уравнение принимает вид:
.
Теорема доказана.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено:
