Дифференциальные уравнения первого порядка
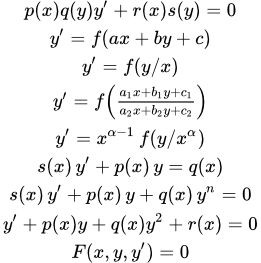
Далее в тексте f , g, p, q, r, s – функции своих аргументов. Штрих ′ означает производную по аргументу. a, b, c, a1 , b1 , c1 , a2 , b2 , c2 , ..., α, β – постоянные.
Дифференциальные уравнения первого порядка, разрешенные относительно производной
Как решать дифференциальные уравнения первого порядка
Пусть мы имеем дифференциальное уравнение первого порядка, разрешенное относительно производной:
f (x, y ) y ′ + g (x, y ) = 0 .
Разделив это уравнение на f (x, y ) , при f (x, y ) ≠ 0 , мы получим уравнение вида:
y ′ = p (x, y ) ,
где p (x, y ) = – g (x, y ) f (x, y ) .
Далее смотрим, не относятся ли эти уравнения к одному из перечисленных ниже типов. Если нет, то перепишем уравнение в форме дифференциалов. Для этого пишем y ′ = dydx и умножаем уравнение на dx . Получаем уравнение в форме дифференциалов:
f (x, y ) dy + g (x, y ) dx = 0 .
Если это уравнение не является уравнением в полных дифференциалах, то считаем, что в этом уравнении y – независимая переменная, а x – это функция от y . Разделим уравнение на dy :
g (x, y ) dxdy + f (x, y ) = 0 .
Далее смотрим, не относится ли это уравнение к одному из, перечисленных ниже типов учитывая, что x и y поменялись местами.
Если и для этого уравнения не найден тип, то смотрим, нельзя ли упростить уравнение простой подстановкой. Например, если уравнение имеет вид:
f (x 2 , y ) dy + g (x 2 , y ) x dx = 0 ,
то замечаем, что x dx = 12 dx 2 . Тогда делаем подстановку t = x 2 . После этого уравнение примет более простой вид:
f (t, y ) dy + 12 g (t, y ) dt = 0 .
Если и это не помогает, то пытаемся найти интегрирующий множитель ⇓.
Уравнения с разделяющимися переменными
p (x ) q (y ) y ′ + r (x ) s (y ) = 0 ;
p (x ) q (y ) dy + r (x ) s (y ) dx = 0 .
Делим на p (x ) s (y ) и интегрируем. При p (x ) s (y ) ≠ 0 получаем:
∫ q (y ) dys (y ) + ∫ r (x ) dxp (x ) = C .
Подробнее >>>
Уравнения, приводящиеся к уравнениям с разделяющимися переменными
y ′ = f (ax + by + c )
Делаем подстановку u = ax + by + c . Тогда
dudx = a + b dydx = a + bf (ax + by + c ) = a + bf (u ) ;
dudx = a + bf (u ) .
Далее разделяем переменные и интегрируем.
Подробнее >>>
Однородные уравнения
y ′ = F ( yx ) , или
f (x, y, y ′ ) = 0 , причем f (tx, ty, y ′ ) = t p f (x, y, y ′ ) .
Решаем подстановкой:
y = u x ,
где u – функция от x . Тогда
y ′ = u ′x + u = f (u ) ;
u ′x = f (u ) – u .
Разделяем переменные и интегрируем.
Подробнее >>>
Уравнения, приводящиеся к однородным
y ′ = F ( a1 x + b1 y + c1 a2 x + b2 y + c2 ) , или
M (a1 x + b1 y + c1 , a2 x + b2 y + c2 ) y ′ + N (a1 x + b1 y + c1 , a2 x + b2 y + c2 ) = 0 ,
где M (u, v ) и N (u, v ) – однородные функции с равными показателями однородности: M (tu, tv ) = t p M (u, v ) , N (tu, tv ) = t p N (u, v ) .
Вводим переменные t и u :
x = t + x0 ;
y = u + y0 .
Постоянные x0 и y0 выбираем так, чтобы свободные члены обратились в нуль:
a1 x + b1 y + c1 = a1 t + b1 u ;
a2 x + b2 y + c2 = a2 t + b2 u .
В результате получаем однородное уравнение в переменных t и u .
Подробнее >>>
Обобщенные однородные уравнения
y ′ = x s – 1 F ( yx s ) , или
f (x, y, y ′ ) = 0 , где f (tx, t s y, t s – 1 y ′ ) = t p f (x, y, y ′ ) .
Делаем подстановку t = x s . Получаем однородное уравнение в переменных t и y .
Подробнее >>>
Линейные дифференциальные уравнения
s (x ) y ′ + p (x ) y = q (x )
Есть три метода решения линейных уравнений.
1) Метод интегрирующего множителя.
Умножаем уравнение на интегрирующий множитель 1s (x ) e ∫ p (x ) s (x ) dx :
y ′e ∫ p (x ) s (x ) dx + y p (x ) s (x ) e ∫ p (x ) s (x ) dx = q (x ) s (x ) e ∫ p (x ) s (x ) dx ;
ddx ( y e ∫ p (x ) s (x ) dx ) = q (x ) s (x ) e ∫ p (x ) s (x ) dx .
Далее интегрируем.
Подробнее >>>
2) Метод Бернулли.
Ищем решение в виде произведения двух функций u = u (x ) и v = v (x ) от переменной x :
y = uv .
s (x ) (u ′v + uv ′ ) + p (x ) uv = q (x ) ;
s (x ) vu ′ + u (s (x ) v ′ + p (x ) v ) = q (x ) .
Одну из этих функций мы можем выбрать произвольным образом. Поэтому в качестве v выбираем любое не нулевое решение уравнения:
s (x ) v ′ + p (x ) v = 0 .
Определив v , получаем уравнение с разделяющимися переменными для u .
Подробнее >>>
3) Метод вариации постоянной (Лагранжа).
Здесь мы сначала решаем однородное уравнение:
s (x ) y ′ + p (x ) y = 0
Общее решение однородного уравнения имеет вид:
y = Cf (x ) ,
где C – постоянная. Далее мы заменяем постоянную C на функцию u = u (x ) , зависящую от переменной x :
C = u (x ) .
Подставляем y = u (x ) f (x ) в исходное уравнение. В результате получаем уравнение, из которого определяем u (x ) .
Подробнее >>>
Уравнения Бернулли
s (x ) y ′ + p (x ) y + q (x ) y n = 0
Подстановкой z = y – n + 1 уравнение Бернулли приводится к линейному уравнению.
Также это уравнение можно решать методом Бернулли. То есть ищем решение в виде произведения двух функций, зависящих от переменной x :
y = uv .
Подставляем в исходное уравнение:
s (x ) (u ′v + uv ′ ) + p (x ) uv + q (x ) u n v n = 0 ;
s (x ) vu ′ + u (s (x ) v ′ + p (x ) v ) + q (x ) u n v n = 0 .
В качестве v выбираем любое не нулевое решение уравнения:
s (x ) v ′ + p (x ) v = 0 .
Определив v = v (x ) , получаем уравнение с разделяющимися переменными для u .
Уравнения Риккати
y ′ + p (x ) y + q (x ) y 2 + r (x ) = 0
Оно не решается в общем виде. Подстановкой
y = A y1 q
уравнение Риккати приводится к виду:
y ′1 + p1 (x ) y1 + Ay 21 + r1 (x ) = 0 ,
где A – постоянная; p1 (x ) = p (x ) – q ′(x ) q (x ) ; r1 (x ) = r (x ) q (x ) A .
Далее, подстановкой:
y1 = y2 – p1 2A
оно приводится к виду:
y ′2 + Ay 22 + r2 (x ) = 0 ,
где r2 (x ) = r1 (x ) – p ′1 2A – p 21 4A .
Свойства уравнения Риккати и некоторые частные случаи его решения представлены на странице
Дифференциальное уравнение Риккати >>>
Уравнения Якоби
(a1 x + b1 y + c1 ) dx + (a2 x + b2 y + c2 ) dy + (a3 x + b3 y + c3 ) (xdy – ydx ) = 0
Решается подстановкой:
x = ξζ , y = ηζ .
Подробнее >>>
Уравнения в полных дифференциалах
p (x, y ) dx + q (x, y ) dy = 0
При условии
∂p∂y = ∂q∂x .
При выполнении этого условия, выражение в левой части равенства является дифференциалом некоторой функции:
p (x, y ) dx + q (x, y ) dy = dU (x, y ) .
Тогда
dU (x, y ) = 0 .
Отсюда получаем интеграл дифференциального уравнения:
U (x, y ) = C .
Для нахождения функции U (x, y ) , наиболее удобным способом является метод последовательного выделения дифференциала. Для этого используют формулы:
du ± dv = d (u ± v ) ;
v du + u dv = d (uv ) ;
v du – u dvv 2 = d ( uv ) ;
f (u ) du = d ( ∫ f (u ) du ) .
Подробнее >>>
Интегрирующий множитель
Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то можно попытаться найти интегрирующий множитель M (x, y ) . Интегрирующий множитель – это такая функцияM (x, y ) , при умножении на которую, дифференциальное уравнение становится уравнением в полных дифференциалах. Дифференциальное уравнение первого порядка имеет бесконечное число интегрирующих множителей. Однако, общих методов для нахождения интегрирующего множителя нет.
Подробнее >>>
Уравнения, не решенные относительно производной y'
Уравнения, допускающие решение относительно производной y'
Сначала нужно попытаться разрешить уравнение относительно производной y ′ . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.
Уравнения, допускающие разложение на множители
Если удастся уравнение разложить на множители:
f 1 (x, y, y ′ ) ⋅ f 2 (x, y, y ′ ) ⋅ f 3 (x, y, y ′ ) ⋅ ... ⋅ f n (x, y, y ′ ) = 0 ,
то задача сводится к последовательному решению более простых уравнений:
f 1 (x, y, y ′ ) = 0 ;
f 2 (x, y, y ′ ) = 0 ;
.....
f n (x, y, y ′ ) = 0 ;
Подробнее >>>
Уравнения, не содержащие x и y
f (y ′ ) = 0
Здесь y ′ – постоянная:
y ′ = a ,
где a – корень уравнения
f (a ) = 0 .
Подробнее >>>
Уравнения, не содержащие x или y
x = g (y ′ ) или y = g (y ′ )
Ищем решение в параметрическом виде. Вводим параметр t . Полагаем y ′ = t . Тогда
x = g (t ) или y = g (t ) .
Далее интегрируем уравнение:
dy = y ′ dx ;
dy = t dx .
В результате получаем выражение второй переменной через параметр t .
Более общие уравнения:
f (x, y ′ ) = 0 или f (y, y ′ ) = 0
также решаются в параметрическом виде. Для этого нужно подобрать такую функцию y ′ = u (t ) , чтобы из исходного уравнения можно было выразить x или y через параметр t .
Чтобы выразить вторую переменную через параметр t , интегрируем уравнение:
dy = y ′ dx ;
dy = u (t ) dx .
Подробнее >>>
Уравнения, разрешенные относительно y
Уравнения Клеро
y = y ′x + f (y ′ )
Такое уравнение имеет общее решение
y = Cx + f (C )
Подробнее >>>
Уравнения Лагранжа
y = f (y ′ ) x + p (y ′ )
Решение ищем в параметрическом виде. Полагаем y ′ = t , где t – параметр.
Подробнее >>>
Уравнения, приводящиеся к уравнению Бернулли
y = xy ′ + x α f (y ′ )
y = xy ′ + y α f (y ′ )
Эти уравнения приводятся к уравнению Бернулли, если искать их решения в параметрическом виде, введя параметр t и делая подстановку y ′ = t .
Подробнее >>>
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: