Решение дифференциальных уравнений с помощью интегрирующего множителя
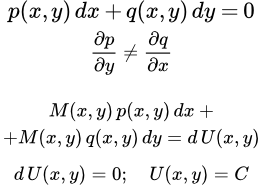
Определение интегрирующего множителя
- Интегрирующий множитель M(x, y)
- – это такая функция от переменных x и y, умножив на которую, дифференциальное уравнение первого порядка
становится уравнением в полных дифференциалах:
Свойства интегрирующего множителя
Рассмотрим дифференциальное уравнение:
(1)
Если
То левая часть уравнения (1) не является дифференциалом некоторой функции. Однако при выполнении условий существования единственного решения уравнения (1), его можно привести к уравнению в полных дифференциалах умножением на некоторую функцию от переменных и .
Теорема о существовании интегрирующего множителя
Пусть для дифференциального уравнения первого порядка выполнены условия существования единственного решения.Тогда оно имеет бесконечное число интегрирующих множителей.
Докажем это. Если существует решение уравнения (1), то его общий интеграл можно представить в виде:
Возьмем дифференциал:
(2)
Отсюда:
С другой стороны, из уравнения (1):
Левые части уравнений равны. Поэтому равны правые части:
Или:
Тогда уравнение (2) можно переписать в виде:
Исходное уравнение (1) превратилось в полный дифференциал умножением на интегрирующий множитель:
что доказывает существование интегрирующего множителя.
Покажем, что существует бесконечно много интегрирующих множителей. Для этого выражение:
Умножим на произвольную функцию от :
Это выражение также является полным дифференциалом, поэтому множитель
также является интегрирующим множителем. Поскольку – это произвольная функция, то можно построить бесконечное число интегрирующих множителей.
Теорема об отношении интегрирующих множителей
Если известны два интегрирующих множителя, отношение которых не является постоянной,то их отношение является общим интегралом дифференциального уравнения:
.
Действительно, поскольку , то
Но, поскольку, – общий интеграл уравнения, то
Отсюда:
Методы определения интегрирующего множителя
Хотя каждое уравнение имеет интегрирующий множитель, совсем не обязательно, что он выражается через известные функции. Поэтому найти интегрирующий множитель можно не всегда. Но даже если интегрирующий множитель выражается через известные функции, нет методов, следуя которыми, можно было бы с гарантией определить его. Поэтому, при решении уравнений, следует проверить, не принадлежит ли уравнение одному из известных типов. И в том случае, если оно не принадлежит ни одному из известных типов, попытаться найти интегрирующий множитель.
Ниже описан ряд методов, с помощью которых, в некоторых случаях, можно найти интегрирующий множитель.
Метод последовательного выделения дифференциала
Этот метод аналогичен методу выделения полного дифференциала для уравнений в полных дифференциалах. Только здесь полный дифференциал удается выделить, умножая уравнение на множители. Для этого применяем формулы дифференцирования, записанные в дифференциальной форме:
;
;
;
.
В этих формулах и – произвольные выражения, составленные из любых комбинаций переменных.
Пример
Решить уравнение:
Решение
Сгруппируем члены:
Замечаем, что
Подставляем и делим на . При уравнение принимает вид:
Но:
;
.
Подставляем:
Отсюда:
.
Мы получили решение, справедливое при . Теперь рассмотрим случай . Нетрудно видеть, что постоянная также является решением уравнения. Поэтому добавим ее в окончательный результат.
Ответ
;
.
В процессе выделения дифференциала мы разделили уравнение на . Поэтому интегрирующий множитель оказался равным
.
Метод группировки членов уравнения
Если сразу найти интегрирующий множитель не удается, то можно попытаться сгруппировать члены уравнения. Пусть мы имеем уравнение:
разбиваем его на сумму слагаемых:
Пусть первое слагаемое имеет интегрирующий множитель:
Умножаем уравнение на :
Далее следует подобрать такую функцию от , чтобы при умножении на нее, второе слагаемое стало полным дифференциалом:
.
Первое слагаемое при этом остается полным дифференциалом:
.
Тогда:
Далее следует подобрать такую функцию от , чтобы при умножении на нее, следующее слагаемое стало полным дифференциалом. И так далее, пока все выражение станет полным дифференциалом.
Пример
Решить уравнение:
Решение
Сгруппируем члены и разделим на :
Первые два члена являются полным дифференциалом:
, подставляем:
Теперь нужно подобрать такую функцию от , чтобы оставшееся выражение стало полным дифференциалом. Методом перебора различных вариантов находим, что для этого нужно разделить уравнение на . Тогда при и уравнение примет вид:
;
;
;
.
Отсюда
.
Теперь рассмотрим случаи и . Зависимости и удовлетворяют исходному уравнению, но не входят в полученный общий интеграл. Поэтому добавим их в окончательный результат.
Ответ
;
;
.
Определение интегрирующего множителя заданного вида
В предыдущем примере мы получили два члена
уравнения, для которых нужно было подобрать интегрирующий множитель вида . Мы это сделали методом подбора. То есть просто угадали, что интегрирующий множитель имеет вид
.
На самом деле процедуры подбора можно избежать. Можно точно определить, имеется ли для заданного уравнения интегрирующий множитель заданного вида. И если имеется, то определить его.
Пусть имеется уравнение
,
для которого ищется интегрирующий множитель вида
где – заданная функция от переменных и .
Найдем такой интегрирующий множитель, или определим, что множителя такого вида не существует.
Для этого умножим исходное уравнение на :
Это уравнение будет уравнением в полных дифференциалах при выполнении условия
.
Или:
;
Теперь положим, что – это функция от , где – это заданная функция переменных и . Тогда
.
Подставляем:
;
.
Отсюда:
(3)
Левая часть этого уравнения является функцией от . Поэтому и правая часть тоже должна быть функцией от .
Таким образом, интегрирующий множитель заданного вида существует, если правая часть уравнения (3) является функцией от u:
В этом случае
Или
Интегрируем:
Отсюда
Поскольку постоянная для интегрирующего множителя никакого значения не имеет, положим :
Пример
Проверить, имеет ли уравнение:
Интегрирующий множитель вида . И если имеет, то найти его.
Решение
В нашем случае:
;
;
;
.
Интегрирующий множитель вида существует, поскольку есть функция от :
Находим его.
;
.
Опускаем знак модуля.
Ответ
Уравнение имеет интегрирующий множитель
.
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
