Дифференциальное уравнение Клеро

Рассмотрен метод решения дифференциального уравнения Клеро и нахождение его особого решения. Дан пример решения дифференциального уравнения Клеро.

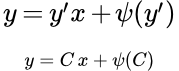
Дифференциальное уравнение Клеро

– это уравнение вида
y = y^′x + ψ (y^′ )  . 

Решение дифференциального уравнения Клеро

Рассмотрим уравнение Клеро:
(1)   y = y^′x + ψ (y^′ ) 
Не трудно убедиться, что его общее решение имеет вид:
(2)   y = Cx + ψ (C ) 

Действительно, поскольку C – постоянная, то ψ (C )  – тоже постоянная. Тогда дифференцируя (2) имеем:
y^′ = (Cx ) ^′ + (ψ (C ) ) ^′ =  C ⋅ (x ) ^′ + 0 = C ⋅ 1 = C ; 
(3)   y^′ = C . 
Подставляя (2) и (3) в (1), получаем тождество:
Cx + ψ (C )  = Cx + ψ (C )  . 

Особое решение дифференциального уравнения Клеро

Уравнение Клеро может иметь особое решение. Как известно, если общее решение дифференциального уравнения имеет вид:
 f (x, y, C )  = 0 , 
то особое решение может получиться исключением C из уравнений:
 f (x, y, C )  = 0 ; 
∂ f ∂C = 0 . 

В нашем случае, решение (2) можно записать в виде:
Cx + ψ (C )  – y = 0 . 
Тогда
 f (x, y, C )  = Cx + ψ (C )  – y . 
Тогда особое решение может получиться, исключением C из уравнений:
y = Cx + ψ (C )  ; 
x + ψ^′(C )  = 0 . 

Поскольку возможны посторонние решения, то после нахождения особого решения, необходимо проверить, удовлетворяет ли он исходному уравнению (1).

Пример

Решить уравнение:
(1.1)   y = xy^′ – a  √ 1 + y^′ 2   

Решение

Это уравнение Клеро. Его общее решение имеет вид:
y = Cx – a  √ 1 + C²   

Ищем особое решение. Перепишем общее решение в виде:
 f (x, y, C )  =  Cx – a  √ 1 + C²   – y = 0 . 
Дифференцируем по C  : 
∂ f ∂C = x – a  ( ( 1 + C²  ) ^1 / 2  ) ^′_C  =  x –  a2 ⋅ ( 1 + C²  ) ^{– 1 / 2}  ⋅ ( 1 + C²  ) ^′_C  = 
 x – a2 ⋅ 1√ 1 + C²    ⋅ 2C =  x – aC√ 1 + C²     . 
Тогда особое решение может получиться исключением C из уравнений:
(1.2)   y = Cx – a  √ 1 + C²    ; 
(1.3)   x – aC√ 1 + C²    = 0 . 

Исключаем C .  Из уравнения (1.3) имеем:
(1.4)   √ 1 + C²   = aCx  . 
Возводим в квадрат и преобразуем:
1 + C²  = a² C² x²   ; 
C² ( a² x²  – 1  )  = 1 ; 
C²  = x² a²  – x²   .  Отсюда следует, что  | x |  <  | a |  . 
Извлекаем квадратный корень:
(1.5)   C = ± x√ a²  – x²     . 
Поскольку мы возводили в квадрат, то, возможно, (1.5) содержит лишние решения, которые не удовлетворяют (1.4). Сейчас мы примем (1.5), а отсев лишних решений сделаем в самом конце.
Подставим (1.4) и (1.5) в (1.2):
y = Cx – a² Cx = C x²  – a² x =  ± x√ a²  – x²    x²  – a² x =  ∓ √ a²  – x²    . 

Итак, особые решения имеют вид:
(1.6)   y = ± √ a²  – x²    . 
Теперь сделаем проверку, чтобы выяснить, удовлетворяет ли исходному уравнению (1.1):
(1.1)   y = xy^′ – a  √ 1 + y^′ 2    . 
Находим производную (1.6) и выполняем преобразования:
y^′ =  ± ( ( a²  – x²  ) ^1 / 2  ) ^′ =  ± 12 ( a²  – x²  ) ^{– 1 / 2}  ( a²  – x²  ) ^′ = 
 ± 12 – 2x√ a²  – x²    = ∓ x√ a²  – x²     ; 
1 + y^′ 2 = 1 + x² a²  – x²  = a² a²  – x²   ; 
√ 1 + y^′ 2  =  | a | √ a²  – x²     . 
Подставляем в (1.1):
(1.7)   ± √ a²  – x²   =  ∓ x² √ a²  – x²    – a | a | √ a²  – x²     . 

При a > 0 ,   | a |  = a .  Уравнение (1.7) принимает вид:
± √ a²  – x²   =  ∓ x² √ a²  – x²    – a² √ a²  – x²    =  – a²  ± x² √ a²  – x²     . 
Оно выполняется, если взять нижний знак:
– √ a²  – x²   = – a²  – x² √ a²  – x²    =  – √ a²  – x²    . 
То есть при a > 0 ,  y = – √ a²  – x²    . 

При a < 0 ,   | a |  = – a .  Уравнение (1.7) принимает вид:
± √ a²  – x²   =  ∓ x² √ a²  – x²    + a² √ a²  – x²    =  a²  ∓ x² √ a²  – x²     . 
Оно выполняется, если взять верхний знак:
+ √ a²  – x²   = a²  – x² √ a²  – x²    =  √ a²  – x²    . 
То есть при a < 0 ,  y = √ a²  – x²    . 

Ответ

Общее решение уравнения имеет вид:
y = Cx – a √ 1 + C²   
При a > 0 уравнение имеет особое решение:
y = – √ a²  – x²    . 

При a < 0 уравнение имеет особое решение:
y = √ a²  – x²    . 

Автор: Олег Одинцов.     Опубликовано: 24-08-2012   Изменено: 10-04-2016