Дифференциальное уравнение Лагранжа
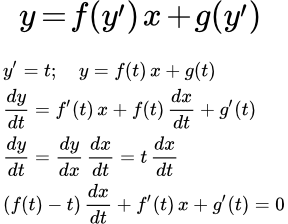
- Дифференциальное уравнение Лагранжа
- – это уравнение вида
y = f (y ′ ) x + g (y ′ ) .
Решение дифференциального уравнения Лагранжа
Рассмотрим дифференциальное уравнение Лагранжа:
(1) y = f (y ′ ) x + g (y ′ ) ,
где f и g – это функции.
Будем искать его решение в параметрическом виде. То есть будем считать, что x , y , а также производная y ′ являются функциями от параметра t . Положим
y ′ ≡ dydx = t .
Поставим в (1):
(2) y = f (t ) x + g (t ) .
Продифференцируем по t :
(3) dydt = f ′(t ) x + f (t ) dxdt + g ′(t ) .
С другой стороны:
(4) dydt = dydx dxdt = t dxdt .
Левые части уравнений (3) и (4) равны. Приравниваем правые части и выполняем преобразования:
f ′(t ) x + f (t ) dxdt + g ′(t ) = t dxdt ;
( f (t ) – t ) dxdt + f ′(t ) x + g ′(t ) = 0 .
Разделим на f (t ) – t . При f (t ) – t ≠ 0 уравнение принимает вид:
dxdt + f ′(t ) f (t ) – t x + g ′(t ) f (t ) – t = 0 .
Это линейное дифференциальное уравнение относительно переменной x . Решая его, получаем зависимость переменной x от параметра t : x = x (t ) . Затем подставляем x = x (t ) в (2):
y = f (t ) x (t ) + g (t ) .
В результате получаем зависимость переменной y от параметра t : y = y (t ) . То есть мы получили параметрическое представление решения уравнения (1).
Дополнительные решения дифференциального уравнения Лагранжа
В процессе приведения уравнения к линейному, мы разделили уравнение на f (t ) – t . Поэтому мы рассматривали решение при f (t ) – t ≠ 0 . В заключении следует рассмотреть случай f (t ) – t = 0 , то есть исключить параметр t из уравнений:
(5) f (t ) – t = 0 ;
(6) y = f (t ) x + g (t ) .
Уравнение (5) содержит только переменную t . Поэтому его нужно решить и определить корни. Если корней нет, то дополнительных решений также нет.
Предположим, что мы нашли корни уравнения (5) (один или несколько). Обозначим такой корень как tk :
(7) f (tk ) – tk = 0 .
Тогда уравнение (6) дает нам зависимость y от x , которая является линейной функцией:
y = f (tk ) x + g (tk ) .
Поскольку в силу (7), f (tk ) = tk , то
(8) y = tk x + g (tk ) .
Покажем, что (8) является решением исходного уравнения (1). Для этого найдем производную (8). Она равна постоянной:
y ′ = tk .
Подставим (8) и y ′ в (1):
y = f (y ′ ) x + g (y ′ ) ;
tk x + g (tk ) = f (tk ) x + g (tk ) ;
tk x = f (tk ) x .
Это уравнение выполняется, поскольку в силу (7), f (tk ) = tk .
Таким образом, мы нашли, что уравнение (1) может иметь решения
y = tk x + g (tk ) ,
где tk – корни уравнения
f (t ) – t = 0 .
Пример
Решить уравнение:
(1.1) 2y (y ′ + 2 ) = xy ′ 2
Решение
Разделим на 2(y ′ + 2 ) . При y ′ ≠ – 2 имеем:
(1.2) y = xy ′ 2 2(y ′ + 2 ) .
Это уравнение Лагранжа. Ищем решение в параметрическом виде. Считаем, что x , y , а также y ′ - это функции от параметра t . Положим y ′ = t . Тогда
(1.3) y = xt 2 2(t + 2 ) .
Чтобы упростить выкладки, умножим (1.3) на знаменатель дроби 2(t + 2 ) и продифференцируем по t :
2(t + 2 ) y = t 2 x ;
2(t + 2 ) ′ y + 2(t + 2 ) dydt = ( t 2 ) ′x + t 2 dxdt ;
(1.4) 2y + 2(t + 2 ) dydt = 2t x + t 2 dxdt .
Далее имеем:
(1.5) dydt = dydx dxdt = t dxdt .
Поставляем (1.3) и (1.5) в (1.4) и выполняем преобразования:
xt 2 t + 2 + 2(t + 2 ) t dxdt = 2t x + t 2 dxdt ;
(t 2 + 4t ) dxdt = 2t (t + 2 ) xt + 2 – xt 2 t + 2 ;
(t 2 + 4t ) dxdt = t 2 + 4tt + 2 x .
Разделим на (t 2 + 4t ) . При t 2 + 4t = t (t + 4 ) ≠ 0 ( или при t ≠ 0 и при t ≠ – 4 ) имеем:
dxdt = xt + 2 .
Разделяем переменные и интегрируем:
dxx = dtt + 2 ;
∫ dxx = ∫ dtt + 2 + C ;
ln | x | = ln | t + 2 | + C .
Потенцируем:
| x | = e C | t + 2 | .
Заменим постоянную ± e C → C . Знак модуля сводится к умножению на постоянную ±1, которую включаем в C .
x = C (t + 2 ) .
Отсюда
t + 2 = xC ;
t = xC – 2 .
Подставляем в (1.3):
y = xt 2 2(t + 2 ) = x ( xC – 2 ) 2 2 xC = C2 ( xC – 2 ) 2 = 12C (x – 2C ) 2 .
Заменим постоянную 2C → C :
y = 1C (x – C ) 2 .
Теперь рассмотрим значения t = y ′ = 0; t = y ′ = – 2; t = y ′ = – 4 , которые мы исключили из рассмотрения при выполнении операций деления. Для этого подставим эти значения в исходное уравнение (1.1),
(1.1) 2y (y ′ + 2 ) = xy ′ 2 .
Проверим, существует ли для этих значений дополнительные решения.
1) Подставим y ′ = 0 в (1.1):
2y (0 + 2 ) = 0 .
Отсюда y = 0 . Решение y = 0 удовлетворяет исходному уравнению (1.1).
2) Подставим y ′ = – 2 в (1.1):
2y (– 2 + 2 ) = x (– 2 ) 2 ;
0 = 4x .
Значение y ′ = – 2 не удовлетворяет исходному уравнению. Отбрасываем его.
3) Подставим y ′ = – 4 в (1.1):
2y (– 4 + 2 ) = x (– 4 ) 2 ;
– 4y = 16x ;
y = – 4x .
Решение y = – 4x удовлетворяет исходному уравнению.
Ответ
Общее решение уравнения имеет вид:
y = 1C (x – C ) 2 ;
y = 0 ;
y = – 4x .
Автор: Олег Одинцов. Опубликовано: Изменено: