Обобщенно однородные дифференциальные уравнения относительно переменных высших порядков

Дано определение и указано как распознать обобщенно однородное относительно переменных дифференциальное уравнение высшего порядка. Приводится подстановка, с помощью которой в этом уравнении можно понизить порядок. Подробно рассмотрен пример решения обобщенно однородного ДУ второго порядка.

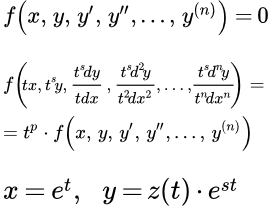
Определения однородных уравнений и функций

Ранее мы рассматривали дифференциальные уравнения высших порядков, однородные относительно функции и ее производных. Теперь рассмотрим уравнения, однородные относительно переменных. Эти уравнения не меняют вид, если сделать замену
x → tx,  y → ty , 
где t – постоянная. Однако мы немного усложним задачу, и будем рассматривать уравнения, которые не меняют вид при замене
(1)   x → tx,  y → t^s y . 
При этом производная порядка m умножается на t^s – m   : 
y^(m )  = d^m y(dx ) ^m  → d^m t^s y(d (tx ) ) ^m  =  t^s t^m  d^m y(dx ) ^m  = t^s – m y^(m )  . 
Такие уравнения называются обобщенными однородными дифференциальными уравнениями высших порядков относительно переменных. Число s называют измерением однородности для переменной y.

Как мы увидим ниже, в таких уравнениях можно понизить порядок с помощью подстановок:
x = ±e^t,   y = ze^st .

Функция, зависящая от производных и переменных, называется обобщенно однородной относительно переменных, если она обладает следующим свойством:
(2)    f ( tx, t^s y, t^s dytdx , t^s d² yt² dx²  ,...   , t^s dⁿ ytⁿ dxⁿ   )  =  t^p  f (x,  y,  y^′,  y^′′,...,  y^(n ) )  , 
где t – произвольное выражение;
Коэффициент p называется показателем однородности функции. Его также называют измерением однородности функции f .

Таким образом, если у нас имеется дифференциальное уравнение
(3)    f (x,  y,  y^′,  y^′′,...,  y^(n ) )  = 0 , 
и при этом функция f обладает свойством (2), то такое уравнение является обобщенно однородным относительно переменных. Действительно, выполнив замену (1) в уравнении (3), и воспользовавшись (2), имеем:
 f (tx, t^s y, t^s – 1 y^′, t^s – 2 y^′′,...  , t^s – n y^(n ) )  = 0 ; 
t^p  f (x,  y,  y^′,  y^′′,...,  y^(n ) )  = 0 ; 
 f (x,  y,  y^′,  y^′′,...,  y^(n ) )  = 0 . 
Постоянная t сократилась. Значит это обобщенно однородное уравнение относительно переменных.

Заметим, что обобщенно однородное уравнение в общем виде можно записать так:
(4)   F ( yx^s  , y^′x^s – 1  , y^′′x^s – 2  , ⋅ ⋅ ⋅   , y^(n ) x^s – n   )  = 0 . 
Это наиболее общая форма записи уравнения, которое не меняет вид при замене (1).

При определении обобщенно однородных уравнений можно рассмотреть и более общую замену
x → t^k x,  y → t^s y , 
введя измерение однородности k и для переменной x . Однако, если принять во внимание, что t^s  = (t^k ) ^s / k  ,  то такая замена сводится к (1) с измерением однородности s / k ,  и поэтому не дает ничего нового.

Как распознать обобщенно однородное относительно переменных дифференциальное уравнение высшего порядка

Чтобы определить, является ли дифференциальное уравнение обобщенно однородным относительно переменных, надо в уравнении выполнить следующие замены:
x → tx,  y → t^s y,  y^′ → t^s – 1 y^′,   y^′′ → t^s – 2 y^′′,  . . .,  y^(n )  → t^s – n y^(n )  . 
Если удастся подобрать такое число s , в результате чего t сократится, то это обобщенное однородное ДУ с измерением однородности s для переменной y .

Пример

Покажем, что следующее уравнение является обобщенно однородным:
(П1)   (xy + x² √ x  ) y^′′ + yy^′ –  x (y^′ ) ²  – 34 y √ x  = 0 . 

Для этого делаем замену (1), и попытаемся найти такое s , при котором t сократится:
x → tx,  y → t^s y ; 
y^′ = dydx → d (t^s y ) d (tx )  =  t^s t dydx = t^s – 1 y^′ ; 
y^′′ = d² y(dx ) ²  → d² (t^s y ) (d (tx ) ) ²  =  t^s t²  d² y(dx ) ²  = t^s – 2 y^′′ ; 
xyy^′′ → txt^s yt^s – 2 y^′′ = t^2s – 1 xyy^′′ ; 
x² √ x  y^′′ = x^{2 + 1 / 2} y^′′ →  (tx ) ^{2 + 1 / 2} t^s – 2 y^′′ = t^{s + 1 / 2} x² √ x  y^′′ ; 
yy^′ → t^s yt^s – 1 y^′ = t^2s – 1 yy^′ ; 
x (y^′ ) ²  → tx (t^s – 1 y^′ ) ²  = t^2s – 1 x (y^′ ) ²  ; 
34 y √ x  → 34 t^s y √ tx  = t^{s + 1 / 2} 34 y √ x   . 
Левая часть уравнения (П1):
(xy + x² √ x  ) y^′′ + yy^′ –  x (y^′ ) ²  – 34 y √ x  → 
 t^2s – 1 xyy^′′ + t^{s + 1 / 2} x² √ x  y^′′ +  t^2s – 1 yy^′ – t^2s – 1 x (y^′ ) ²  –  t^{s + 1 / 2} 34 y √ x   . 
Для того, чтобы множители, содержащие t можно было вынести за скобки, они должны быть равны:
t^2s – 1  = t^{s + 1 / 2}  = t^2s – 1  =  t^2s – 1  = t^{s + 1 / 2}  . 
Отсюда
2s – 1 = s + 1 / 2 ; 
s = 1 + 1 / 2 = 3 / 2 . 
Таким образом, при s = 3 / 2 все множители, содержащие t равны t²  .  Поэтому их можно сократить, в результате чего уравнение (П1) сохранит свой вид. Это означает, что уравнение (П1) является обобщенно однородным уравнением относительно переменных с измерением однородности для переменной y , s = 3 / 2 .  При этом функция
 f (x,  y,  y^′,  y^′′ )  =  (xy + x² √ x  ) y^′′ + yy^′ –  x (y^′ ) ²  – 34 y √ x  
имеет показатель однородности p = 2 (или измерение однородности p = 2).

В заключение, приведем исходное уравнение к виду (4), выполняя преобразования.
 f (x,  y,  y^′,  y^′′ )  =  (xy + x² √ x  ) y^′′ + yy^′ –  x (y^′ ) ²  – 34 y √ x  = 
 ( x^5 / 2 yx^3 / 2  + x^5 / 2  ) x^{– 1 / 2} y^′′x^{– 1 / 2}  +  x² yx^3 / 2  y^′x^1 / 2  – x ⋅ x ( y^′x^1 / 2   ) ²  –  34 x^3 / 2 yx^3 / 2  x^1 / 2  = 
 x² [ ( yx^3 / 2  + 1  ) y^′′x^{– 1 / 2}  +  yx^3 / 2  y^′x^1 / 2  – ( y^′x^1 / 2   ) ²  – 34 yx^3 / 2   ]  = 
 x² F ( yx^3 / 2  , y^′x^1 / 2  , y^′′x^{– 1 / 2}   )  = 0 . 
Отсюда получаем уравнение
F ( yx^3 / 2  , y^′x^1 / 2  , y^′′x^{– 1 / 2}   )  = 0 , 
где F (u, v, w )  =  (u + 1 ) w + uv – v²  – 34 u . 

Метод решения обобщенно однородных уравнений

Обобщенно однородное уравнение приводится к уравнению, не содержащему независимую переменную, при помощи подстановки:
(2.1)   x = e^t ,  y = ze^st  при x > 0 , 
или x = – e^t ,  y = ze^st  при x < 0 . 
Здесь t – новая независимая переменная; z – новая зависимая переменная, то есть функция от t :
z = z (t )  . 
Зависимость y (x )  определяется из (2.1) в параметрическом виде.

После подстановки (2.1) в исходное уравнение, множители, содержащие переменную t , сокращаются, и мы получаем дифференциальное уравнение, не содержащее в явном виде зависимую переменную t . Далее приводится пример решения такого уравнения.

Пример

Решить уравнение:
(П2.1)   (xy + x² √ x  ) y^′′ + yy^′ –  x (y^′ ) ²  – 34 y √ x  = 0

Решение

В первом примере ⇑ мы показали, что это обобщенно однородное уравнение относительно переменных с измерением однородности для переменной y,  s = 3 / 2 .  Понижаем его порядок с помощью (2.1).

Поскольку в исходное уравнение входит √ x   ,  то оно определено при x ≥ 0 .  Делаем подстановку
(П2.2)   x = e^t ,  y = ze^3t / 2  . 
Здесь t – новая независимая переменная; z – зависимая переменная, то есть функция от t :
z = z (t )  . 

Подставляем x,  y,  y^′,  y^′′ ,  выраженные через t,  z ,  и производные z по t в исходное уравнение (П2.1).
(xy + x² √ x  ) y^′′ =  (e^t ze^3t / 2  + e^2t e^t / 2 )  ⋅  ( z^′′ + 2z^′ + 34 z  ) e^{– t / 2}  = 
 (z + 1 ) ( z^′′ + 2z^′ + 34 z  ) e^2t  ; 
yy^′ = ze^3t / 2 ( z^′ + 32 z  ) e^t / 2  =  z ( z^′ + 32 z  ) e^2t  ; 
x (y^′ ) ²  = e^t ( z^′ + 32 z  ) ² e^t  =  ( z^′ + 32 z  ) ² e^2t  ; 
y √ x  = ze^3t / 2 e^t / 2  = ze^2t  ; 
(xy + x² √ x  ) y^′′ + yy^′ – x (y^′ ) ²  –  34 y √ x  = 
 (z + 1 ) ( z^′′ + 2z^′ + 34 z  ) e^2t  +  z ( z^′ + 32 z  ) e^2t  –  ( z^′ + 32 z  ) ² e^2t  – 34 ze^2t  = 0 . 
Сокращаем множитель e^2t  и выполняем дальнейшие преобразования.
(z + 1 ) ( z^′′ + 2z^′ + 34 z  )  +  z ( z^′ + 32 z  )  –  ( z^′ + 32 z  ) ²  – 34 z = 0 ; 
(z + 1 ) z^′′ + 2(z + 1 ) z^′ +  34 z (z + 1 )  + zz^′ + 32 z²  – z^′ 2 –  3zz^′ – 94 z²  – 34 z = 0 ; 
(П2.4)   (z + 1 ) z^′′ + 2z^′ – z^′ 2 = 0 . 

Мы получили дифференциальное уравнение, не содержащее зависимую переменную t в явном виде. Делаем подстановку
(П2.5)   u = z^′ ≡ dzdt  . 
Теперь мы считаем, что независимой переменной является z ,  а зависимой – u . То есть u – является функцией от z  : 
u = u (z )  . 
Выражаем вторую производную z по t через переменные z и u , применяя правило дифференцирования сложной функции, и применяя (П2.5).
z^′′ ≡ dz^′dt = dudt = dudz ⋅ dzdt = dudz ⋅ u ; 
z^′′ = u dudz  . 
Подставляем в (П2.4).
(z + 1 ) u dudz + 2u – u²  = 0 . 

Делим на u . При u ≠ 0 имеем:
(z + 1 ) dudz + 2 – u = 0 . 

В переменных z и u мы получили дифференциальное уравнение первого порядка. Разделяем переменные и интегрируем.
(z + 1 ) dudz = u – 2 ; 

Делим на (z + 1 ) (u – 2 )  .  При z ≠ – 1,  u ≠ 2 имеем:
duu – 2 = dzz + 1  ; 
∫ duu – 2 = ∫ dzz + 1 + C₁  ; 
ln  | u – 2 |  = ln  | z + 1 |  + C₁  . 
Потенцируем.
 | u – 2 |  =  | z + 1 |  ⋅ e^C₁  . 
Раскрытие знаков модулей эквивалентно умножению на постоянную + 1 или – 1 .  Заменим постоянную: ± e^C₁  → C₁  . 
u – 2 = C₁ (z + 1 )  . 

Переходим к переменным t и z ,  подставляя u = dzdt  . 
dzdt – 2 = C₁ (z + 1 )  . 
Разделяем переменные и интегрируем.
dzdt = C₁ z + C₁  + 2 . 

При C₁ z + C₁  + 2 ≠ 0 имеем:
dzC₁ z + C₁  + 2 = dt ; 
∫ dzC₁ z + C₁  + 2 = ∫ dt + C₂  ; 
1C₁  ∫ d (C₁ z + C₁  + 2 ) C₁ z + C₁  + 2 = t + C₂  ; 
1C₁  ln  | C₁ z + C₁  + 2 |  = t + C₂  ; 
ln  | C₁ z + C₁  + 2 |  = C₁ t + C₁ C₂  . 
Потенцируем.
 | C₁ z + C₁  + 2 |  = e^C₁ t e^C₁ C₂  . 
Заменим постоянную ± e^C₁ C₂  → C₂  и выполняем преобразования.
C₁ z + C₁  + 2 = C₂ e^C₁ t  ; 
z = C₂ C₁  e^C₁ t  – 1 – 2C₁   . 
Снова заменим постоянную C₂ C₁  → C₂  . 
z = C₂ e^C₁ t  – 1 – 2C₁   . 

Переходим к переменным x и y , используя (П2.2).
y = ze^3t / 2  =  ( C₂ e^C₁ t  – 1 – 2C₁   ) e^3t / 2  =  ( C₂ (e^t ) ^C₁  – 1 – 2C₁   ) (e^t ) ^3 / 2  = 
 ( C₂ x^C₁  – 1 – 2C₁   ) x^3 / 2  ; 
(П2.6)   y = ( C₂ x^C₁  – 1 – 2C₁   ) x^3 / 2  . 

Теперь рассмотрим случаи u = 0 ⇑, z = – 1 ⇑, u = 2 ⇑, C₁ z + C₁  + 2 = 0 ⇑, которые мы исключили при выполнении операций деления.

1) Рассмотрим случай u = 0 .  Отсюда
z^′ = u = 0,  z = C – произвольная постоянная. Тогда
(П2.7)   y = ze^3t / 2  = Cx^3 / 2  . 
Подстановкой можно убедиться, что z^′ = 0 удовлетворяет уравнению (П2.4). Поэтому (П2.7) является решением исходного уравнения (П2.1).

Однако почти все решения вида (П2.7) уже включены в (П2.6) при C₂  = 0 .  Из уравнения – 1 – 2C₁  = C можно определить C₁  для всех C , кроме значения C = – 1  :  C₁  = – 2C + 1  .  Поэтому к решению вида (П2.6) нужно добавить только одно решение (П2.7) с C = – 1  : 
y = – x^3 / 2  . 

2) Рассмотрим случай z = – 1 .  При этом
y = ze^3t / 2  = – x^3 / 2  . 
Это решение мы уже добавили.

3) Рассмотрим случай u = 2  : 
z^′ = u = 2 ; 
z = 2t + C ; 
(П2.8)   y = ze^3t / 2  = (2t + C ) e^3t / 2  =  (2 ln x + C ) x^3 / 2  . 
Можно убедиться, что z^′ = 2 удовлетворяет уравнению (П2.4). Поэтому (П2.8) является решением исходного уравнения (П2.1).

4) Рассмотрим случай C₁ z + C₁  + 2 = 0 .  Отсюда
z = – 1 – 2 / C₁  ; 
Выше мы рассмотрели более общий случай z = C .  Поэтому здесь ничего нового нет.

Ответ

y = ( C₂ x^C₁  – 1 – 2C₁   ) x^3 / 2  ; 
y = – x^3 / 2  ; 
y = (2 ln x + C ) x^3 / 2  . 

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов.     Опубликовано: 19-11-2021