Пределы монотонных функций
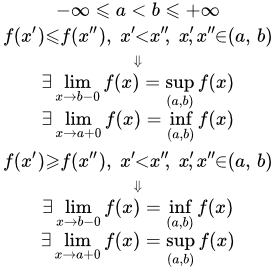
Определения
- Возрастающая и убывающая функции
- Пусть функция f(x) определена на некотором множестве действительных чисел X .
Функция называется строго возрастающей (строго убывающей), если для всех x′, x′′ ∈ X таких что x′ < x′′ выполняется неравенство:
f(x′) < f(x′′) ( f(x′) > f(x′′) ).
Функция называется неубывающей (невозрастающей), если для всех x′, x′′ ∈ X таких что x′ < x′′ выполняется неравенство:
f(x′) ≤ f(x′′) ( f(x′) ≥ f(x′′) ).
Отсюда следует, что строго возрастающая функция также является неубывающей. Строго убывающая функция также является невозрастающей.
- Монотонная функция
- Функция называется монотонной, если она неубывающая или невозрастающая.
Для исследования монотонности функции f (x ) на некотором множестве X , нужно найти разность ее значений в двух произвольных точках x ′′ > x ′ , принадлежащих этому множеству. Если f (x ′′ ) – f (x ′ ) > 0 , то функция строго возрастает; если f (x ′′ ) – f (x ′ ) ≥ 0 , то функция не убывает; если f (x ′′ ) – f (x ′ ) < 0 , то строго убывает; если f (x ′′ ) – f (x ′ ) ≤ 0 , то не возрастает.
Если на некотором множестве функция положительна: f (x ) > 0 , то для определения монотонности, можно исследовать частное от деления ее значений в двух произвольных точках x ′′ > x ′ этого множества. Если f (x ′′ ) f (x ′ ) > 1 , то функция строго возрастает; если f (x ′′ ) f (x ′ ) ≥ 1 , то функция не убывает; если f (x ′′ ) f (x ′ ) < 1 , то строго убывает; если f (x ′′ ) f (x ′ ) ≤ 1 , то не возрастает.
Теорема о пределе монотонной функции
Пусть функция f(x) не убывает на ограниченном или неограниченном интервале (a, b) , где – ∞ ≤ a < b ≤ + ∞ .Если она ограничена сверху числом M : f (x ) ≤ M ,
то существует конечный левый предел в точке b : limx → b – 0 f (x ) ≤ M .
Если f(x) не ограничена сверху,
то limx → b – 0 f (x ) = + ∞ .
Если f(x) ограничена снизу числом m : f (x ) ≥ m ,
то существует конечный правый предел в точке a : limx → a + 0 f (x ) ≥ m .
Если f(x) не ограничена снизу,
то limx → a + 0 f (x ) = – ∞ .
Если точки a и b являются бесконечно удаленными, то в выражениях под знаками пределов подразумевается, что + ∞ – 0 = + ∞; – ∞ + 0 = – ∞ .
Эту теорему можно сформулировать более компактно.
Тогда существуют односторонние пределы в точках a и b :
limx → b – 0 f (x ) = sup(a,b ) f (x ) ;
limx → a + 0 f (x ) = inf(a,b ) f (x ) .
Аналогичная теорема для невозрастающей функции.
Тогда существуют односторонние пределы:
limx → b – 0 f (x ) = inf(a,b ) f (x ) ;
limx → a + 0 f (x ) = sup(a,b ) f (x ) .
Тогда в любой точке x0 ∈ (a, b ) из этого интервала, существуют односторонние конечные пределы функции f (x ) :
limx → x0 – 0 f (x ) и limx → x0 + 0 f (x ) .
Доказательство теоремы
Функция не убывает
b – конечное число
Функция ограничена сверху
1. Пусть функция f (x ) не убывает на интервале (a, b ) .
1.1. Пусть число b конечное: b ≠ + ∞ .
1.1.1. Пусть функция ограничена сверху числом M : f (x ) ≤ M при x ∈ (a, b ) .
Докажем, что в этом случае существует предел limx → b – 0 f (x ) = sup(a,b ) f (x ) .
Поскольку функция ограничена сверху, то существует конечная верхняя грань
sup(a,b ) f (x ) = B ≤ M .
Согласно определению точной верхней грани, выполняются следующие условия:
f (x ) ≤ B для всех x ∈ (a, b ) ;
для любого положительного ε > 0 существует такой аргумент xε ∈ (a, b ) , для которого
f (xε ) > B – ε ; или
B – f (xε ) < ε .
Поскольку функция не убывает, то f (x ) ≥ f (xε ) при x > xε . Тогда
B – f (x ) < ε при xε < x < b .
Преобразуем последнее неравенство:
xε < x < b ;
– xε > – x > – b ;
b – xε > b – x > 0 ;
0 < b – x < b – xε .
Поскольку f (x ) ≤ B , то B – f (x ) = | f (x ) – B | . Тогда
| f (x ) – B | < ε при 0 < b – x < b – xε .
Обозначим δε = b – xε . Тогда для любого ε > 0 существует δε > 0 , так что
| f (x ) – B | < ε при 0 < b – x < δε .
Это означает, что предел слева в точке b равен B = sup(a,b ) f (x ) (см. «Определения односторонних пределов функции в конечной точке»).
Функция не ограничена сверху
1. Пусть функция f (x ) не убывает на интервале (a, b ) .
1.1. Пусть число b конечное: b ≠ + ∞ .
1.1.2. Пусть функция f (x ) не ограничена сверху.
Докажем, что в этом случае существует предел limx → b – 0 f (x ) = sup(a,b ) f (x ) = + ∞ .
Поскольку функция не ограничена сверху, то для любого числа M существует такой аргумент xM ∈ (a, b ) , для которого
f (xM ) > M .
Поскольку функция не убывает, то f (x ) ≥ f (xM ) при x > xM . Тогда f (x ) > M при xM < x < b . Или
f (x ) > M при 0 < b – x < b – xM .
Обозначим δM = b – xM . Тогда для любого M существует δM > 0 , так что
f (x ) > M при 0 < b – x < δM .
Это означает, что предел слева в точке b равен + ∞ (см. «Определения односторонних бесконечных пределов функции в конечной точке»).
b рано плюс бесконечности
Функция ограничена сверху
1. Пусть функция f (x ) не убывает на интервале (a, b ) .
1.2. Пусть число b равно плюс бесконечности: b = + ∞ .
1.2.1. Пусть функция ограничена сверху числом M : f (x ) ≤ M при x ∈ (a, + ∞ ) .
Докажем, что в этом случае существует предел limx → + ∞ f (x ) = sup(a, + ∞ ) f (x ) .
Поскольку функция ограничена сверху, то существует конечная верхняя грань
sup(a, + ∞ ) f (x ) = B ≤ M .
Согласно определению точной верхней грани, выполняются следующие условия:
f (x ) ≤ B ;
для любого положительного ε > 0 существует такой аргумент xε ∈ (a, + ∞ ) , для которого
f (xε ) > B – ε ; или
B – f (xε ) < ε .
Поскольку функция не убывает, то f (x ) ≥ f (xε ) при x > xε . Тогда B – f (x ) < ε при x > xε . Или
| f (x ) – B | < ε при x > xε .
Итак, мы нашли, что для любого ε > 0 существует число xε , так что
| f (x ) – B | < ε при x > xε .
Это означает, что предел при x → + ∞ равен B = sup(a, + ∞ ) f (x ) (см. «Определения односторонних пределов на бесконечности»).
Функция не ограничена сверху
1. Пусть функция f (x ) не убывает на интервале (a, b ) .
1.2. Пусть число b равно плюс бесконечности: b = + ∞ .
1.2.2. Пусть функция f (x ) не ограничена сверху.
Докажем, что в этом случае существует предел limx → + ∞ f (x ) = sup(a, + ∞ ) f (x ) = + ∞ .
Поскольку функция не ограничена сверху, то для любого числа M существует такой аргумент xM ∈ (a, + ∞ ) , для которого
f (xM ) > M .
Поскольку функция не убывает, то f (x ) ≥ f (xM ) при x > xM . Тогда f (x ) > M при x > xM .
Итак, для любого M существует число xM , так что
f (x ) > M при x > xM .
Это означает, что предел при x → + ∞ равен + ∞ (см. «Определения односторонних бесконечных пределов на бесконечности»).
Функция не возрастает
Теперь рассмотрим случай, когда функция f (x ) не возрастает. Можно, как и выше, рассмотреть каждый вариант по отдельности. Но мы охватим их сразу. Для этого используем универсальное определение предела функции по Коши. Докажем, что в этом случае существует предел limx → b – 0 f (x ) = inf(a,b ) f (x ) .
Рассмотрим конечную нижнюю грань множества значений функции:
inf(a,b ) f (x ) = B .
Здесь B может быть как конечным числом, так и бесконечно удаленной точкой – ∞ . Согласно определению точной нижней грани, выполняются следующие условия:
f (x ) ≥ B ;
для любой окрестности U(B ) точки B существует такой аргумент xU ∈ (a, b ) , для которого
f (xU ) ∈ U(B ) .
По условию теоремы, a < x < b . Поэтому xU < b .
Поскольку функция не возрастает, то f (x ) ≤ f (xU ) при x > xU . Поскольку f (x ) ≥ B , то
B ≤ f (x ) ≤ f (xU ) при xU < x < b .
Или
f (x ) ∈ U(B ) при xU < x < b .
Далее замечаем, что неравенство xU < x < b определяет левую проколотую окрестность точки b .
Итак, мы нашли, что для любой окрестности точки B = inf(a,b ) f (x ) , существует такая проколотая левая окрестность ○WU (b – 0 ) точки b , что
f (x ) ∈ U(B ) при x ∈ ○WU (b – 0 ) .
Это означает, что предел слева в точке b равен B = inf(a,b ) f (x ) :
limx → b – 0 f (x ) = inf(a,b ) f (x )
(см. универсальное определение предела функции по Коши).
Предел в точке a
Теперь покажем, что существует предел в точке a и найдем его значение.
Рассмотрим функцию g(x ) = f (– x ) . Несложно видеть, что она определена при x ∈ (– b, – a ) . Если f (x ) не убывает, то g(x ) не возрастает. И наоборот, если f (x ) не возрастает, то g(x ) не убывает.
Применим для функции g(x ) доказанную часть теоремы.
Если f (x ) не убывает, то g(x ) не возрастает. Тогда существует предел
(A.1) limx → – a – 0 g(x ) = inf(– b, – a ) g(x ) .
Если f (x ) не возрастает, то g(x ) не убывает. В этом случае существует предел
(A.2) limx → – a – 0 g(x ) = sup(– b, – a ) g(x ) .
Представим функцию f (x ) = g(– x ) как сложную:
f (x ) = g(t(x )) , где t(x ) = – x .
Воспользуемся теоремой о пределе сложной функции.
Функция t = t(x ) = – x отображает правостороннюю проколотую окрестность точки a , x > a , на левостороннюю проколотую окрестность точки – a, t < – a . Поскольку существуют пределы limx → a + 0 t(x ) = – a – 0 , и limt → – a – 0 g(t ) , то существует предел сложной функции
limx → a + 0 f (x ) = limx → a + 0 g(t(x )) = limt → – a – 0 g(t ) .
Учитывая (A.1) и (A.2) мы приходим к следующему.
Если f (x ) не убывает, то существует предел
(A.3) limx → a + 0 f (x ) = inf(– b, – a ) g(x ) .
Если f (x ) не возрастает, то существует предел
(A.4) limx → a + 0 f (x ) = sup(– b, – a ) g(x ) .
Поскольку множества значений функций f и g совпадают, то их нижние и верхние грани равны:
inf(– b, – a ) g(x ) = inf(a,b ) f (x ); sup(– b, – a ) g(x ) = sup(a,b ) f (x ) .
Тогда от (A.3) и (A.4) мы приходим к тому, что (A.3) требовалось доказать.
Если f (x ) не убывает, то существует предел
limx → a + 0 f (x ) = inf(a,b ) f (x ) .
Если f (x ) не возрастает, то существует предел
limx → a + 0 f (x ) = sup(a,b ) f (x ) .
Теорема доказана.
Автор: Олег Одинцов. Опубликовано: Изменено: