Окрестность точки

Рассмотрено общее определение окрестности точки на числовой прямой. Определения эпсилон окрестности, левосторонней, правосторонней и проколотых окрестностей конечных и бесконечно удаленных точек. Свойство окрестности. Доказана теорема о равносильности использования эпсилон окрестности и произвольной окрестности в определении предела функции по Коши.

Содержание

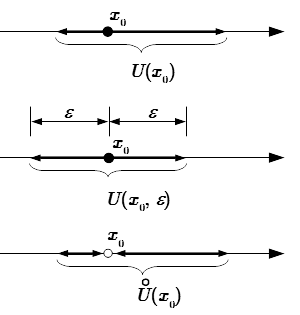
Определение окрестности точки

Окрестность действительной точки: Окрестностью действительной точки x₀ называется любой открытый интервал, содержащий эту точку:
.
Здесь ε₁ и ε₂ – произвольные положительные числа.
Эпсилон окрестность точки: Эпсилон окрестностью точки x₀ называется множество точек, расстояние от которых до точки x₀ меньше ε:
.
Проколотая окрестность точки: Проколотой окрестностью точки x₀ называется окрестность этой точки, из которой исключили саму точку x₀:
.

Окрестности конечных точек

В самом начале было дано определение окрестности точки. Ее обозначают как . Но можно явно указать, что окрестность зависит от двух чисел, используя соответствующие аргументы:
(1) .
То есть окрестность – это множество точек, принадлежащее открытому интервалу .

Приравняв ε₁ к ε₂, получим эпсилон - окрестность:
(2) .
Эпсилон - окрестность – это множество точек, принадлежащее открытому интервалу с равноудаленными концами.
Разумеется, букву эпсилон можно заменить на любую другую и рассматривать δ - окрестность, σ - окрестность, и т.д.

В теории пределов можно использовать определение окрестности, основанное как на множестве (1), так и на множестве (2). Использование любой из этих окрестностей дает эквивалентные результаты (см. теорему ниже ⇓). Но определение (2) проще, поэтому часто используют именно эпсилон - окрестность точки, определяемую из (2).

Также широко используют понятия левосторонних, правосторонних и проколотых окрестностей конечных точек. Приводим их определения.

Левосторонняя окрестность действительной точки x₀: – это полуоткрытый интервал, расположенный на действительной оси слева от точки x₀, включая саму точку:
;
.
Правосторонняя окрестность действительной точки x₀: – это полуоткрытый интервал, расположенный справа от точки x₀, включая саму точку:
;
.

Проколотые окрестности конечных точек

Проколотые окрестности точки x₀ – это те же самые окрестности, из которых исключена сама точка. Они обозначаются с кружочком над буквой. Приводим их определения.

Проколотая окрестность точки x₀: .
Проколотая эпсилон окрестность точки x₀: ;
.
Проколотая левосторонняя окрестность: ;
.
Проколотая правосторонняя окрестность: ;
.

Окрестности бесконечно удаленных точек

Наряду с конечными точками, также вводят понятие окрестности бесконечно удаленных точек. Все они являются проколотыми, поскольку не существует бесконечно удаленного действительного числа (бесконечно удаленная точка определяется как предел бесконечно большой последовательности).

.
;
;
.

Можно было определить окрестности бесконечно удаленных точек и так:
.
Но вместо M мы используем , чтобы окрестность с меньшим ε являлась подмножеством окрестности с большим ε, как и для окрестностей конечных точек.

Свойство окрестности

Далее мы используем очевидное свойство окрестности точки (конечной или бесконечно удаленной). Оно заключается в том, что окрестности точек с меньшими значениями ε являются подмножествами окрестностей с большими значениями ε. Приводим более строгие формулировки.

Пусть есть конечная или бесконечно удаленная точка. И пусть .
Тогда
;
;
;
;
;
;
;
.

Также справедливы и обратные утверждения.

Эквивалентность определений предела функции по Коши

Теперь покажем, что в определении предела функции по Коши, можно использовать как произвольную окрестность , так и окрестность с равноудаленными концами .

Теорема
Определения предела функции по Коши, в которых используются произвольные окрестности и окрестности с равноудаленными концами эквивалентны.

Доказательство

Сформулируем первое определение предела функции.
Число a является пределом функции в точке (конечной или бесконечно удаленной), если для любых положительных чисел существуют такие числа , зависящие от и , что для всех , принадлежит соответствующей окрестности точки a:
.

Сформулируем второе определение предела функции.
Число a является пределом функции в точке , если для любого положительного числа существует такое число , зависящее от , что для всех :
.

Доказательство 1 ⇒ 2

Докажем, что если число a является пределом функции по 1-му определению, то оно также является пределом и по 2-му определению.

Пусть выполняется первое определение. Это означает, что имеются такие функции и , так что для любых положительных чисел выполняется следующее:
при , где .

Поскольку числа и произвольные, то приравняем их:
.
Тогда имеются такие функции и , так что для любого выполняется следующее:
при , где .

Заметим, что .
Пусть есть наименьшее из положительных чисел и . Тогда, согласно отмеченному выше свойству ⇑,
.
Если , то .

То есть мы нашли такую функцию , так что для любого выполняется следующее:
при , где .
Это означает, что число a является пределом функции и по второму определению.

Доказательство 2 ⇒ 1

Докажем, что если число a является пределом функции по 2-му определению, то оно также является пределом и по 1-му определению.

Пусть выполняется второе определение. Возьмем два положительных числа и . И пусть – наименьшее из них. Тогда, согласно второму определению, имеется такая функция , так что для любого положительного числа и для всех , следует, что
.

Но согласно свойству окрестностей ⇑, . Поэтому из того, что следует, что
.

Тогда для любых положительных чисел и , мы нашли два числа , так что для всех :
.

Это означает, что число a является пределом и по первому определению.

Теорема доказана.

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.

Автор: Олег Одинцов. Опубликовано: 23-04-2018