Определение предела функции в конечной точке

Даны определения пределов функции в конечной точке по Коши. Рассмотрены определения двусторонних и односторонних пределов (слева и справа). Также приводятся определения бесконечных пределов в конечной точке. Разобраны примеры решений задач, в которых требуется показать, что предел равен заданному значению, используя определение Коши.

Содержание

См. также:

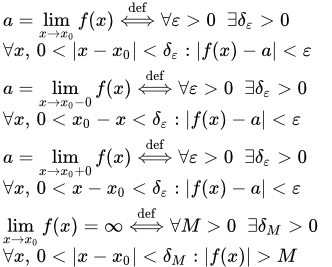
Определение предела функции по Коши

Конечный предел функции в конечной точке

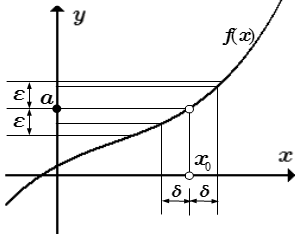
Предел функции в точке по Коши — Предел функции в точке:
|f(x) – a| < ε при 0 < |x – x₀| < δ

Конечный предел функции по Коши: Число a называется пределом функции f(x) в точке x₀, если
1) существует такая проколотая окрестность конечной точки x₀, на которой функция определена;
2) для любого сколь угодно малого положительного числа ε > 0 существует такое число δ_ε > 0, зависящее от ε, что для всех x, принадлежащих проколотой δ_ε - окрестности точки x₀: 0 < |x – x₀| < δ_ε, значения функции принадлежат ε - окрестности точки a:
|f(x) – a| < ε.
Предел функции обозначается так:
.
Или при .

С помощью логических символов существования и всеобщности определение предела функции можно записать следующим образом:
.

Односторонние пределы

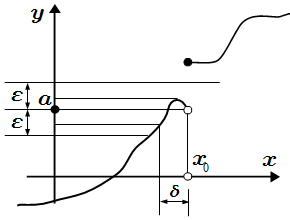
Левый предел функции в точке по Коши — Левый предел функции в точке:
|f(x) – a| < ε при 0 < x₀ – x < δ

Функция может быть определена не с двух сторон от точки , а в некоторой левой окрестности точки , при или в некоторой правой окрестности, при . Также функция может иметь разрыв в точке . Тогда используют односторонние пределы.

Левый предел в точке (левосторонний предел):
.
Правый предел в точке (правосторонний предел):
.
Пределы слева и справа часто обозначают так:
; .

Бесконечный предел функции в конечной точке

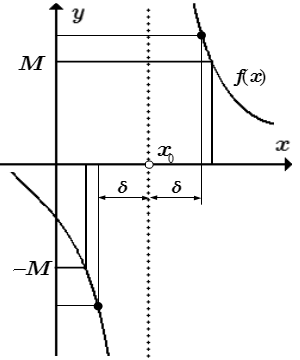
Бесконечный предел функции в точке по Коши — Бесконечный предел функции в точке:
|f(x)| > M при 0 < |x – x₀| < δ

Бесконечный предел функции по Коши: Предел функции f(x) при x → x₀ равен бесконечности, если
1) существует такая проколотая окрестность конечной точки x₀, на которой функция определена;
2) для любого, сколь угодно большого числа M > 0, существует такое число δ_M > 0, зависящее от M, что для всех x, принадлежащих проколотой δ_M - окрестности точки x₀: 0 < |x – x₀| < δ_M, значения функции принадлежат окрестности бесконечно удаленной точки:
|f(x)| > M.
Бесконечный предел обозначают так:
.
Или при .

С помощью логических символов существования и всеобщности определение бесконечного предела функции можно записать так:
.

Также можно ввести определения бесконечных пределов определенных знаков, равных и :
.
.

Аналогичным образом вводятся определения односторонних пределов.
Левые пределы.
.
.
.
Правые пределы.
.
.
.

Определение предела функции по Гейне

Предел функции по Гейне: Число a (конечное или бесконечно удаленное) называется пределом функции f(x) в точке x₀:
,
если
1) существует такая проколотая окрестность точки x₀, на которой функция определена;
2) для любой последовательности {x_n}, сходящейся к x₀: ,
элементы которой принадлежат окрестности , последовательность {f(x_n)} сходится к a:
.

Если в качестве окрестности взять левостороннюю окрестность точки x₀, то получим определение левого предела. Если правостороннюю – то получим определение правого предела.

Определения предела по Гейне и Коши эквивалентны.

Примеры

Все примеры Далее мы приводим подробные решения задач, в которых нужно показать существование пределов, используя определение предела по Коши.
⇓, ⇓, ⇓.

Пример 1

Все примеры ⇑ Используя эпсилон и дельта - рассуждения показать, что
.

Решение

Введем обозначения:
.
Выпишем определение конечного предела функции в точке по Коши:
.
Преобразуем разность:

.

Пусть
.
Тогда
;
;
.

Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .

Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .

Пример 2

Все примеры ⇑ Используя определение предела по Коши показать, что
.

Решение

Введем обозначение:
.
Выпишем определение предела функции в точке , равного бесконечности, по Коши:
.
Выразим многочлены в числителе и знаменатели через многочлены от .
;
.

Пусть
.
Тогда
;

;
.

Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .

Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .

Пример 3

Все примеры ⇑ Используя определение предела по Коши показать, что
.

Решение

Введем обозначение:
.
Выпишем определение левого предела в точке , равного , по Коши:
.
В нашем случае .
Выразим многочлены в числителе и знаменатели через многочлены от .
;

.

Пусть
.
Тогда
; ;
;
;
.

Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .

Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов. Опубликовано: 12-05-2018

См. также: